惯导滤波参数优化算法

高伟伟， 朱文杰， 方 丹， 王 毅， 田 杰

(陆军工程大学石家庄校区 四系，河北 石家庄 050003)

0 引 言

为了抑制惯导解算参数受积累性误差的影响，往往采用组合的方法提高导航系统性能，如卫星与惯导组合、星光与惯导的组合等[1]。组合系统的核心是误差的估计与修正，一般采用基于Kalman 滤波的误差估计方法，相关参数的误差估计过程是否收敛，估计速度如何，估计精度怎样均会影响组合系统的性能[2～5]。在误差估计过程中，滤波参数的设置是影响误差估计速度和精度的关键因素，因此，本文对捷联惯导组合滤波参数优化方法进行了研究。

1 Kalman滤波修正方法

由于惯性系统随时间增长会产生误差积累，在实际工程应用中，需要监测捷联姿态测量系统各误差状态量的变化，根据状态数值变化大小对系统进行干预和修正。各误差状态量中，有些状态可通过仪器测量直接得到，但测量得到的数值中通常有测量噪声，且一般不能满足所有状态均可通过仪器测量，这就需要通过最优估计方法实现。最优估计方法通过建立状态方程和量测方程，对部分可测量状态数据进行数学处理，得到某种估计准则下误差最小的更多状态估值，常用的最优估计方法有Kalman滤波估计，它是一种递推线性最小方差估计[6～9]。

以Kalman 滤波闭环校正为例，对误差状态量的修正过程如图1所示。根据各误差参数对输出结果的影响程度，选取适当的误差参数作为状态量，并建立误差状态方程，结合外部参考信息和捷联数学解算信息建立量测方程

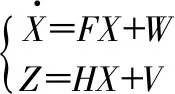
(1)

通过观测量采用Kalman估计出主要误差状态参数值，并对捷联数学解算过程进行误差修正[10,11]，因此，误差修正的关键是如何实现相关参数误差的准确估计。在Kalman 滤波估计过程中，滤波参数初值P0，Q0，R0的设定将影响误差状态量的估计速度、精度以及系统的稳定性[10,11]。由于实际应用中无法准确获得过程噪声Wk和量测噪声Vk的统计特性，大多情况下通过实际系统的先验值或实测数据得到P0，Q0，R0的大概取值范围[12]。如何合理设置滤波参数初值，以最大程度上改善并发挥Kalman滤波估计性能，是提高系统精度的关键环节[13]。

图1 基于Kalman滤波的误差状态修正过程

2 初始滤波参数的优化

为分析滤波参数初值对滤波性能的影响，以陆基条件下的姿态误差估计为例，选取速度误差、姿态误差、位置误差、加速度计零偏、陀螺零偏为状态量，且设状态量

X=[δVEδVNφEφNφUδLδλρEρNεE

εNεU]

设初始条件下，三轴陀螺的常值零偏均为0.1°/h，随机噪声0.05°/h，三轴加速度计的常值零偏为100 gn，随机噪声为50 gn，速度误差均为0.1 m/s，位置误差均为100 m，初始俯仰角误差为5′，横滚角误差为15′，方位角误差为15′；以东向和北向速度误差为观测量，设定量测误差均为标准差为0.01 m/s的零均值高斯噪声。载体初始条件下处于静止状态，10 s后以0.5 m/s2的加速度向北行驶，20 s后停止加速并匀速运动至第120 s结束，滤波周期为0.1 s。根据以上仿真条件，通常情况下Kalman 滤波初始参数设定如下：

P0=diag[(0.1 m/s)2,(0.1 m/s)2,(5′)2,(5′)2,(15′)2,(100 m)2,(100 m)2,(100gn)2,(100gn)2,(0.1°/h)2,(0.1°/h)2,(0.1°/h)2]

Q0=diag[(50 gn)2,(50 gn)2,(0.05°/h),(0.05°/h),(0.05°/h),0,0,0,0,0,0,0]

R0=diag[(0.01 m/s)2,(0.01 m/s)2]

在以上条件下，得到的姿态误差估计曲线如图2所示。整理Kalman滤波估计结果得到，上述初始滤波参数条件下，俯仰角和横滚角误差在静态条件下即可估计，且120 s内估计精度在0.5′以内，方位角误差在北向加速激励后可估计，120 s内的估计精度在1′左右。由于在捷联姿态解算过程中，方位角精度受总体误差源的影响较大，因此,本文以方位角的误差估计为例，在设置不同的初始参数值条件下，通过仿真分析揭示不同滤波参数对姿态误差估计的影响。

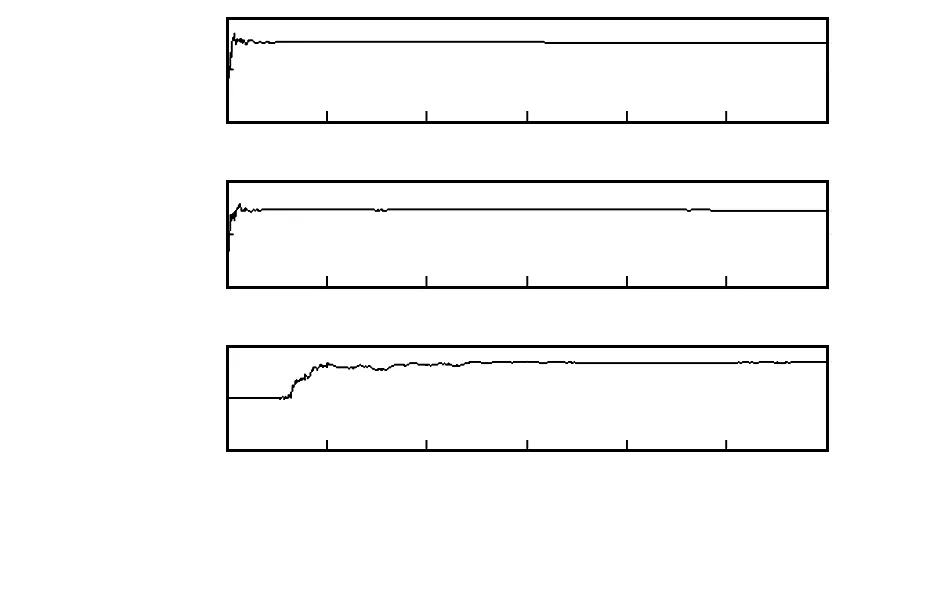
图2 姿态误差估计结果

1)不同P/Q/R值对误差状态估计的影响

在保持其它条件不变得情况下，设定P初值分别为P0,0.1P0,0.5P0,5P0,20P0，得到方位角误差估计结果如图3所示。分析仿真结果可得，较大的P值可提高方位角误差估计速度，但收敛过程具有较大震荡；较小的P值时，方位角误差估计速度较慢，但收敛过程较稳定，具有较好的抗干扰能力。

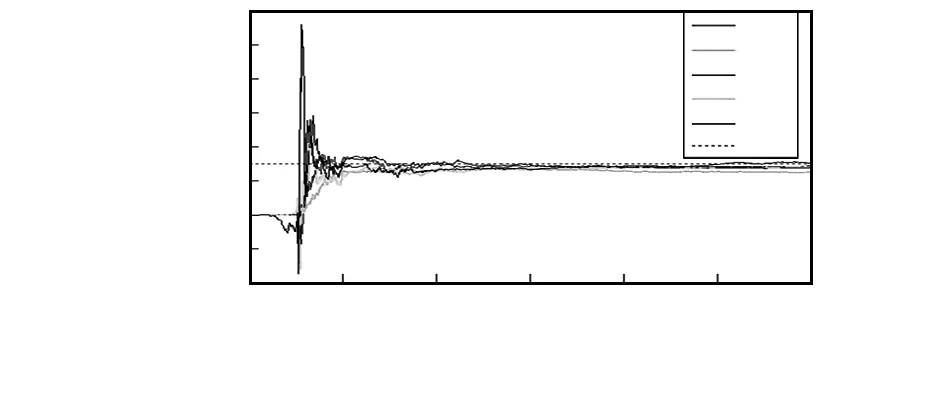
图3 不同P值下的方位角误差估计

在保持其它条件不变得情况下，设定Q初值分别为Q0,0.01Q0,0.1Q0,5Q0,20Q0，得到方位角误差估计结果如图4所示。

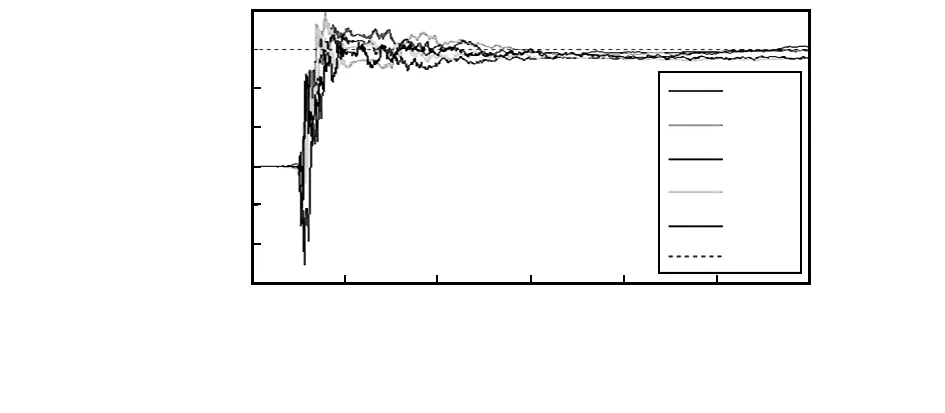
图4 不同Q值下的方位角误差估计

分析结果可知较大的Q值将影响方位角误差的估计精度，引起较大的估计误差；较小的Q值有利于提高估计精度。

同理，设定R初值分别为R0,0.01R0,0.1R0,5R0,20R0，得到方位角误差估计结果如图5所示。从图中可看出，较小的R值将引起较大的震荡，不利于系统的稳定性；过大的R值将引起较大的估计误差；适当增大R值有利于提高系统的稳定性和估计精度。

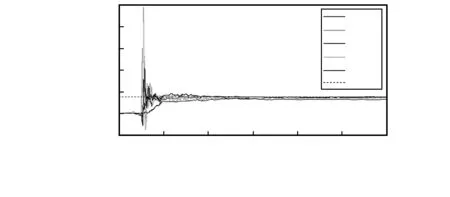
图5 不同R值下的方位角误差估计

2)滤波参数值的优化

综合上一节的分析结果，在实际应用中，为提高滤波估计精度以及系统的稳定性，可设置较小的P值、Q值及较大的R值。设优化后的滤波参数P=0.5P0，Q=0.5Q0，R=2R0，非优化滤波参数P=5P0，Q=5Q0，R=0.1R0，标准滤波参数P=P0，Q=Q0，R=R0；在上述参数设置条件下，得到方位角的误差估计结果如图6所示。从图中可看出，参数优化后方位角误差估计过程更加平稳，且在120内可达到较高的估计精度，相比标准滤波参数输出精度提高了0.5′。

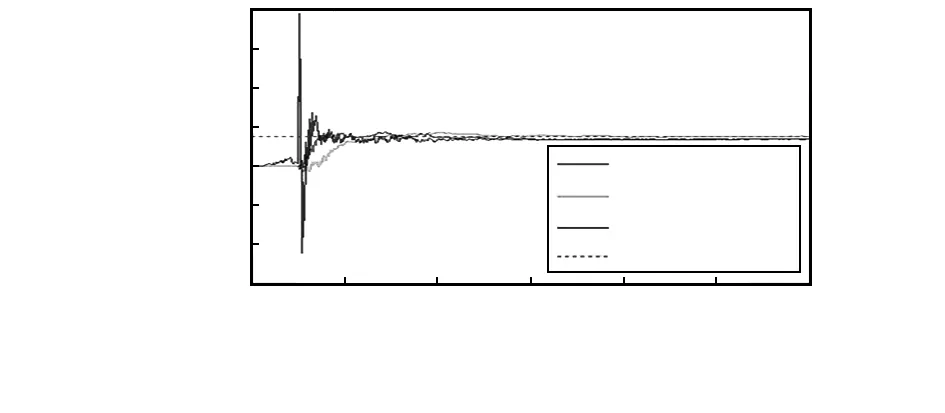
图6 滤波参数优化前后的方位角误差估计

3 结 论

惯导误差修正效果如何涉及多方面的因素，其中滤波参数的设置是重要因素之一。惯导滤波参数优化方法研究为初始滤波参数的设置提供了参考依据，有助于通过初始滤波参数的设置提高滤波估计性能，进而提高惯导误差修正效果。结合工程实验效果和仿真变化规律，可为实际应用中初始滤波参数的设置提供经验依据。