基于肤色模型与BP神经网络的手势识别*

张彩珍， 张云霞， 赵 丹, 张晓金

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

0 引 言

随着人工智能和计算机视觉技术的不断发展，人机交互技术成为计算机领域研究的热点，其中手势是一种直观自然的交流方式，手势识别亦是研究的重点[1,2]。手势识别的研究现主要有数据手套和基于计算机视觉的手势识别技术，基于数据手套的识别需用户佩戴复杂的设备，不大方便且成本高，因而基于计算机视觉的识别技术因便捷性和开发成本低受到了人们的青睐。由于手势动作易变和外界环境因素的影响，目前较为普遍的识别方式是将肤色和形状轮廓特征结合到一起进行识别。谭台哲等人结合深度信息与肤色信息分割出手势区域，提出一种基于形状特征的手势识别方法[3]，王兵等人利用Kinect设备捕获到手部区域,采用隐马尔科夫模型识别手势[4]，王海鹏等人提出了一种基于动态时间规整(dynamic time warping,DTW)方法的时空多尺度手势识别方法——SDTW(spatial-temporal DTW)[5]，杨红玲等人提出一种基于YCbCr空间肤色分割去除背景结合卷积神经网络进行手势识别的方法[6]，张墨逸等人提出了一种基于单应的目标运动轨迹观测模型，利用移动相机进行手势轨迹识别的方法[7]，上述算法对手势均有不错的识别效果，但大多是针对特定场景，对于基于单目摄像头的手势识别时，识别具有一定的局限性。

本文提出了一种能应用于不同环境下的基于肤色模型与BP神经网络的手势识别算法。

1 基于离散余弦变换边缘检测和YCbCr空间肤色的手势分割

手势分割算法主要分为基于肤色、轮廓和运动三种，因手势图像的特殊性，目前大多采用肤色分割，而好的肤色模型需要一个能聚簇且与非肤色的重叠部分少的彩色空间；在YCbCr空间，肤色在复杂背景和不同光照条件下能很好的聚簇在一个类椭圆范围内，能较好地限制肤色的限制区域，但也易受到类肤色区域的干扰，因而提出一种结合离散余弦变换(discrete cosine transform,DCT)进行边缘检测和YCbCr空间肤色模型分割手势的方法。

1.1 DCT滤波去噪与边缘检测

一般采集到的图像均或多或少含有噪声，分割前需对图片进行滤波处理；数字图像都是实数矩阵，在式(1)的DCT中，随着u,v的增大，其对应的余弦函数频率也随之增大，过程中得到的系数称为低频系数、中频系数和高频系数；一般图像的DCT低频和高频系数分别在DCT系数矩阵的左上角和右下角位置，图像中的噪声通常属于高频部分，可通过二维DCT把高频部分屏蔽掉进而抑制噪声。

二维DCT

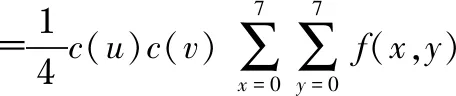
cos((2x+1)uπ/16)cos((2y+1)vπ/16)

(1)

二维DCT逆变换

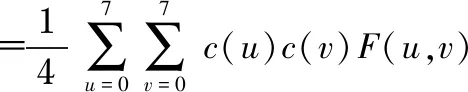
cos((2x+1)uπ/16)cos((2y+1)vπ/16)

步骤2 按顺序逐次比较两次装试序列Si和Sj中相互对应的任务节点th和tk(th,tk∈EngineTask)，若th,tk关联的质量表相同，则比较下一任务节点；否则将th,tk及其对应的质量表分别添入Ψi,Ψj。

(2)

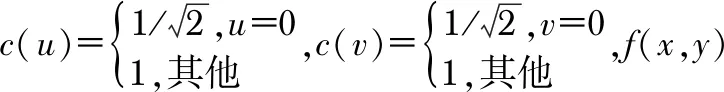
对式(2)求梯度得

(3)

通过对式(3)进行一系列的简化近似运算，即得到一个Hs和Hc的边缘检测矩阵算子，梯度公式可写成

(4)

根据式(4)可计算出梯度算子，继而计算出图像f(x,y)中点的模值，再与边缘检测的阈值T相比判断是否为边缘点，检测出所有的边缘点。

1.2 肤色模型分割和形态学处理

YCbCr空间中的Y为流明(luminance)，表示光的浓度，Cb和Cr分别为蓝色与红色的浓度偏移量成份。因一般图像为RGB色彩空间，需转换到YCbCr空间[9，10]

(5)

将肤色映射到YCbCr空间，得到一个CbCr的椭圆，判断坐标(Cb,Cr)是否在椭圆内(包括边界)即可判断是否为肤色像素点。形成的统计椭圆模型具体如下

(6)

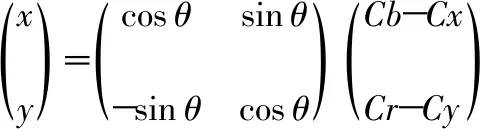
(7)

肤色检测时可能会受到图片中其他物体的影响，分割出非手势区域，通过比较分割出的区域，去除少像素连通区域，得到分割出的手势；对分割出的肤色区域进行形态学闭运算处理，填充空洞使轮廓更清晰。这里a=644.652 1，b=196.840 9，Cx=109.38，Cy=152.02，eCx=1.60，eCy=2.41。手势分割提取的过程如图1所示。

图1 YCbCr手势分割过程

将两种检测结果相与结合，可提取出无干扰的手势；为测验分割算法的效果，本文针对不同背景和亮度下1～10的手势进行了分割，分割结果如图2所示；从图2的分割结果图可看出，手势在复杂背景和有与肤色相近物体干扰的情况下依然能很好的从图片中分割出来。

图2 手势分割结果

2 手势特征提取

加速稳健特征(speeded up robust features，SURF)是SIFT算法的改进，改善了特征提取和描述方式，提升了算法执行速度，是一种局部特征点检测和描述算法[11]，具有图像缩放、旋转、仿射变换保持不变性的特性，有较好的鲁棒性且运算速度快，常被应用于目标识别、图像匹配、图像分析等领域。结合SURF算法的特点，对前面分割出的手势提取特征点，具体算法流程图如图3所示。

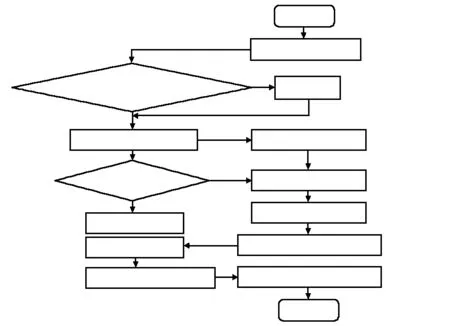
图3 SURF算法流程

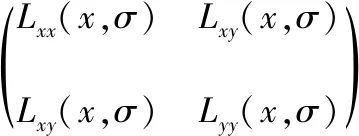
图4 匹配结果图

将特征点的数据进行归一化处理，获得的部分特征点的值如表1所示。

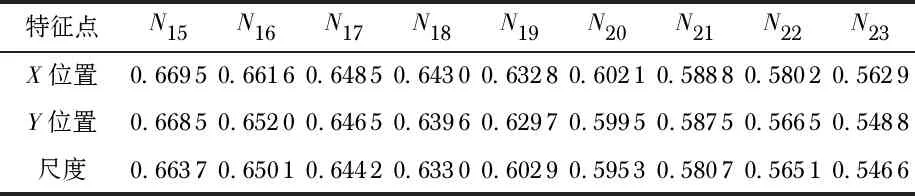
表1 部分特征值

3 基于BP神经网络进行手势识别

BP神经网络因其良好的非线性映射能力、自学习和自适应能力成为目前应用最多的神经网络[12～15]，分为正向传播和反向传播两个过程，当正向传播的输出结果未达到期望值时，开始反向传播。为了提高手势的识别率，本文基于BP神经网络建立了手势识别分类器。

对不同样本，设输入为xi=[xi1,xi2,…,xim]，输入层m与隐藏层j之间的权值为wmj，隐藏层j与输出层k之间的权值为vjk，采用ReLU函数作为激励函数。

隐藏层神经元的输入和输出分别

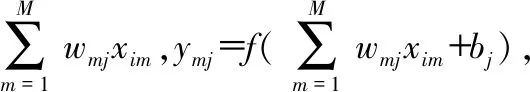
i=1,2,…

(8)

输出层神经元的输入和输出分别为

(9)

隐藏层到输出层的权值更新为

Δvjk=ηδkYk,vjk(n+1)=vjk(n)+Δvjk

(10)

输入层到隐藏层的权值更新为

Δwmj=ηδkymj,wmj(n+1)=wmj(n)+Δwmj

(11)

式中η为学习率，通过调整学习率，反复迭代使网络的实际输出与期望输出逐步的逼近，达到所要求的结果。在训练完网络之后，将测试样本正向传播，最后到达输出层节点，输出识别结果。针对之前提取出的特征点进行一个三层神经网络模型的搭建，输出的类别向量为：y=diag{1,1,…,1}，分别对应1～10的手势数字。从输入到输出所构建的网络模型如图5所示。

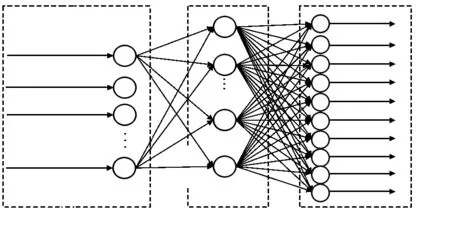
图5 神经网络模型搭建

4 实验过程和结果分析

对本文提出的识别方法在不同的数据库中进行验证，一种是在室内采集拍摄组成的手势图像数据库，采集不同环境、不同光照和角度下的10种类别手势图像各100张，用于算法性能的测试，另一种是Thomas Moeslund’s Gesture Recognition Database数据库。从采集到的手势图片中选取3 000个训练样本和100个测试样本。

因之前提取的每个特征点有着3个描述特性，故选择输入层神经元个数为90，网络的隐藏层神经元个数为15，输出层神经元个数为10个，对应表示1～10的手势，采用全连接的方式；经迭代训练，得到不同的训练次数与手势识别率和误差的关系，如图6所示。这里BP算法的学习率预先设为0.01。

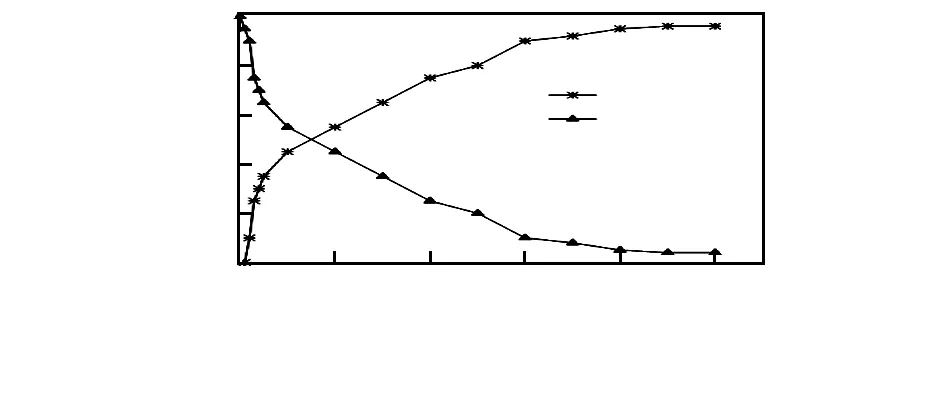
图6 手势训练次数与识别率和误差值关系

由图6可以看出，随着训练次数的增加，手势识别率在不断提高，而识别误差相应的减小，当训练次数达到900次时，识别率达到了最高，误差值到最低。为验证本文算法的性能，通过算法获取结果的识别率与其他算法的识别率进行了比较，本文算法、文献[10]、文献[12]、文献[13]、文献[14]的识别率分别为96 %,94.1 %,95 %,91.7 %,90.35 %。

5 结 论

经对比发现本文算法的识别率较高，本文将DCT算法用于滤波和边缘检测，结合肤色模型提取出的手势效果佳，且算法使用的神经网络结构简单，在计算上缩短了时间，在提取特征值时采用了SURF算法，能够完善提取出手势特征，为之后的训练识别提供了有效的输入，使得识别率得以提高。