基于弹簧系数的无线传感器网络定位算法

朱慧勇, 单志龙

(1.西安铁路职业技术学院 牵引动力学院,陕西 西安 710026；2.华南师范大学 计算机学院,广东 广州 510631)

0 引 言

在无线传感器网络[1]中,如何用少量锚节点的位置信息来定位大量未知节点的位置是无线传感器网络的重点技术之一。距离矢量跳(distance vector hop,DV-Hop)算法[2]对锚节点数量要求少,算法简单,满足无线传感器网络部署低成本、节能高效的要求,成为了众多基于非测距定位算法中的研究热点。在DV-Hop算法中,用锚节点之间的信息来计算平均跳距,但得到的平均跳距有较大误差；用节点之间的最小跳数来表示两个节点之间的关系,没有细化；用平均跳距与最小跳数的乘积来表示距离,没有更为精确的表示节点之间的估计距离。

针对这些问题,已有的众多DV-Hop改进算法主要是采用加权或者优选锚节点的方法来提高精度。文献[3]使用接收信号强度指示(received signal strength indication,RSSI)确定节点之间的分数跳数,得到修正后的平均跳距,采用无约束优化方法进行定位计算。文献[4]以基于加权误差修正的信标节点平均跳距之和为平均跳距,并采用改进的最小二乘法对累积定位误差进行处理。文献[5]利用RSSI测距技术得到相邻节点之间的距离,进行辅助定位,并利用未知节点的质心坐标对自己的初始定位结果进行修正,然后利用修正后的坐标重新定位未知节点。上述改进算法主要都是从局部进行改进,虽然得到了一些好的结果,但都没有从全局进行考虑。文献[6]通过筛选参与锚节点平均跳距计算的锚节点减小引入误差,并对其进行加权处理以提高精度。文献[7]根据不同平均跳距处的RSSI值,选取最大平均跳距、最小平均跳距处、通信半径处的RSSI值,求出比例因子,再利用该比例因子求出加权系数来修正每一跳数。文献[8]利用 RSSI 测距来确定与信标节点距离较近的未知节点的位置,将其升级为信标节点,从而增加信标节点的数目；在计算未知节点坐标时,采用自由搜索的算法代替误差较大的三边测量法。

本文提出的基于弹簧系数和RSSI的DV-Hop改进算法(spring coefficient and RSSI DV-Hop,SCRDH)算法将节点与锚节点间最短路径抽象成弹簧模型,然后利用弹簧模型改进了DV-Hop全网平均跳距和节点之间最小跳数的取值方法,并通过增加全网弹簧系数来提高定位精度。

1 SCRDH算法

本文从全局出发,将节点与锚节点间最短路径抽象成弹簧模型,利用锚节点之间的弹簧模型建立全网的平均弹簧系数,并将弹簧系数应用到全网中进行定位。

1.1 弹簧模型

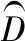
图1 锚节点A与锚节点B的最短路径

(1)

1.2 SCRDH定位算法

针对DV-Hop算法平均跳距、最小跳数和估计距离3个方面的问题,对提出的SCRDH算法进行改进。

1.2.1 计算全网的平均跳距

为了更方便地估计全网的平均跳距,将全网距离划分为5个等级[9],分别为0.2R,0.4R,0.6R,0.8R,R,其中,R为传输半径。先分别求出节点之间距离为0.2R,0.4R,0.6R,0.8R时,节点收到信号的功率值p1,p2,p3,p4。当节点收到其他节点信号的功率p时,与p1,p2,p3,p4进行比较,得到节点之间的等级距离

(2)

当所有节点都知道其与邻居节点的距离d时,统计5个等级的个数,做出等级分布如表1。

表1 距离d等级分布

其中,Pt是第t等级的个数与全部等级个数的比值。则全网的平均跳距可表示为

(3)

节点A收到它的邻居节点B发送的信息后,将功率转化为等级距离,并且按格式(节点B的标示符,距离等级dBA)将信息存储下来,节点A的邻居节点有可能不止节点B一个,同样,节点A也把其它的邻居节点的信息存储下来。当所有节点都把自己的邻居节点存储下来后,并且汇总给汇聚节点,汇聚节点计算出全网的平均跳距。汇聚节点再将平均跳距再反馈给每个节点。

1.2.2 计算未知节点到锚节点的最小跳数

锚节点C按格式(锚节点C的标识符,坐标,跳数Hop)发送消息给邻居节点D,节点D根据之前存储的信息(锚节点C的标识符,距离等级dCD)与刚收到的信息进行处理,得到(锚节点C的标识符,坐标,Hop=Hop+dCD)信息,存储并转发给节点D的邻居节点。重复以上步骤,直到所有节点都具有锚节点的位置信息和彼此间的最小跳数。广播时,跳数Hop初始值为0,节点只保留与锚节点最小跳数的信息,其他消息抛弃掉,减少通信开销。

1.2.3 计算全网的平均弹簧系数

(4)

式中Hopij为锚节点i和锚节点j的最小跳距,其求解方法同1.2.2节计算未知节点到锚节点的最小跳数。

由式(1),锚节点i和锚节点j之间的弹簧系数kij为

(5)

通过求平均值计算出锚节点i的平均弹簧系数

(6)

式中m为锚节点的个数。

根据每个锚节点的平均弹簧系数,汇总给汇聚节点,汇聚节点对其求均值作为全网的平均弹簧系数K反馈给全网的节点

(7)

1.2.4 计算未知节点的位置坐标

经过信息交换后,未知节点i存储的信息包含有全网的平均跳距、全网的平均弹簧系数K和到锚节点的最小跳数Hopi,根据弹簧模型,未知节点到锚节点的估计距离为

(8)

当未知节点获取3个或以上锚节点的估计距离后,根据三边定位法或最小二乘法即可估计出未知节点位置。

2 仿真结果与分析

本文使用MATLAB对SCRDH算法和DV-Hop算法进行了仿真。仿真环境为100 m×100 m的区域,无线传感器节点随机分布在区域中。锚节点的个数为5个,通信半径为20 m,节点总数为100个。为了抑制随机分布产生的误差,所得仿真结果均为相同参数下仿真100次的平均值。

2.1 锚节点个数

图2为不同距离等级与不同锚节点数目对DV-Hop算法、SCRDH算法定位精度的影响。随着锚节点个数的增加,SCRDH算法和DV-Hop算法的定位精度都随之提高。当锚节点达到15个时,定位精度的提高基本保持稳定。SCRDH算法的定位精度优于DV-Hop算法,当锚节点个数为25时,SCRDH算法按6个等级的定位精度比DV-Hop算法提高了15 %。按6个等级SCRDH算法使全网的平均跳距更精确一点,最小跳数更细化了,因此,SCRDH算法比DV-Hop算法更精确。

图2 按不同等级划分定位精度比较

2.2 通信半径

图3(a)为不同通信半径对SCRDH算法与DV-Hop算法定位误差的影响,其中锚节点数15个,节点总数为100个。节点通信半径越大,DV-Hop算法与SCRDH算法的定位精度也就越高。当通信半径为24 m时,二种算法的定位精度提高的幅度基本保持稳定。通信半径增加,网络节点的连通度增加,定位精度也就提高了。从图中也可看出,SCRDH算法明显优于DV-Hop算法。

图3(b)为节点通信半径对SCRDH算法定位精度的影响。节点通信半径越大,SCRDH算法的定位精度也就越高。当通信半径为25 m时,算法的定位精度提高的幅度最大。当锚节点个数为10以后,定位精度的提高幅度趋于渐缓。当锚节点个数为15时,SCRDH算法通信半径20 m时的定位误差为29 %,而SCRDH算法通信半径30 m时的定位误差为12 %。定位误差12 %说明SCRDH算法是非常可行的。通信半径增加,网络节点的连通度增加,计算全网的平均跳距、最小跳数,更精确,定位精度更提高。

图3 通信半径对定位精度影响

2.3 节点数量

图4(a)与图4(b)分别是节点总数为150，200时,两种算法定位误差的比较。当节点总数一定时,锚节点的个数增加时两种算法的定位精度都有所提高。SCRDH算法的定位精度比DV-Hop算法那至少提高20 %。

图4 节点总数为150和200时两种算法定位误差比较

当传感器网络中节点总数增加时,SCRDH算法的定位精度也随之提高,特别是节点总数由100个变为150个时,算法的定位精度得到大幅度的提高,如图5所示。当锚节点个数为15时,SCRDH算法的定位精度提高幅度逐渐变小；当节点总数增加时,节点的连通度变大,有利于节点定位。

图5 节点数量变化时定位误差比较

3 结 论

将节点与锚节点间最短路径抽象成弹簧模型,利用弹簧模型改进了DV-Hop全网平均跳距,以及节点到节点的最小跳数的取值方法,并通过增加全网弹簧系数提高了定位精度。仿真结果表明：SCRDH算法明显优于DV-Hop算法；SCRDH算法的定位误差在一定条件下可以达到12 %。