基于自适应参数的非局部立体匹配算法*

敖小乐,贺继林,邓 宇,2, 李成雷

(1.中南大学 机电工程学院,湖南 长沙 410083；2.湖南山河科技股份有限公司, 湖南 株洲 412002)

0 引 言

立体匹配是机器视觉领域中的一个基础问题,其核心是通过查找双目或多目图像的对应像素点来计算视差,进而获得所拍摄场景的深度信息。目前在自动驾驶、虚拟现实、机器人导航等领域均有广泛应用[1]。Scharstein D等人[2]对典型的立体匹配算法进行了深入研究,将立体匹配分为代价计算、代价聚合、视差选择/优化、视差修正四个过程。根据视差优化方法的不同,立体匹配可分为全局算法和局部算法两类。全局算法通过构造能量最小化函数求取视差,算法精度高,但计算量大、实时性差。局部算法利用窗口内邻域信息来计算单像素视差,相比全局算法,具有计算复杂度低、效率高等优点,但存在窗口选择难题,且其计算复杂度与所选窗口相关。

代价计算用来度量左右图像对应像素的相似性,常见的有绝对亮度差(absolute brightness difference,AD)、梯度、Census变换等代价,Hirschmuller H等人[3,4]对这些匹配代价进行了详细的评述。目前,多数立体匹配算法选择融合多种匹配代价,Mei X等人[5]对AD和Census代价进行线性融合；Fan H R等人[6]对Census和梯度代价进行融合。结果表明对多种代价进行融合能够兼顾不同匹配代价的优点,可以取得更高的精度以及更强的鲁棒性。

为提高信噪比,局部算法假定同一窗口内像素具有相似的视差,用窗口内像素代替单个像素代价,也即代价聚合。常用方法有引导图滤波[7]、十字交叉窗口聚合[8]等,但这些方法仍然受到支持窗口的限制,使得精度难以提升。Yang Q[9]提出非局部算法,通过构造图像的最小生成树(minimum spanning tree,MST),在图像全局范围内进行像素代价聚合,在时效性以及精确性上都取得了较好的结果。基于此,Mei等人[10]提出分割树(segment tree,ST)算法,Yao P等人[11]提出MST-CD算法均表明,基于最小生成树的代价聚合方法要优于其他局部算法。

本文提出一种融合多种代价的改进非局部立体匹配算法；增强了算法在低纹理区域表现,提高了视差精度。

1 算法描述

1.1 代价计算

传统的非局部算法对RGB颜色代价和水平方向梯度代价进行线性融合

(1)

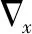
由于该匹配代价只利用了水平方向梯度,忽略了垂直方向梯度包含的丰富信息；此外由于两截断阈值τAD,τGRDX不一致,该融合代价无法直观体现两代价实际所占比重。针对这些问题,本文先融入垂直方向梯度,并对各代价做归一化处理,再进行线性融合

C′(p,p′)=α·ρ[CAD(p,p′),τAD]+β·ρ[CGRDX(p,p′),τGRDX]+(1-α-β)·ρ[CGRDY(p,p′),τGRDY]

(2)

式中α,β∈(0,1)用来平衡各代价比重；CGRDY(p,p′)为垂直方向梯度代价；各匹配代价归一化计算公式为

ρ(C,τ)=1-e(-C/τ)

(3)

经过以上归一化处理并线性融合后,匹配代价被映射到(0,1)区间。为进一步增强算法在低纹理区域表现,对融合后代价进行对数变换

C(p,p′)=ln(1+eC′(p,p′))

(4)

C(p,p′)即为最终匹配代价。上式中,当代价趋于0时,该变换函数能够将值为零的代价转换为非零代价ln 2,从而提高低纹理区域像素对代价聚合的贡献；而当代价逐渐增大时,该函数则愈趋近于C′(p,p′),这样便能保持高纹理区域代价的区分性。

1.2 代价聚合

文献[9]中,图像被看作是一幅四连通或八连通的无向图G=(V,E),V为无向图顶点,为图像像素点集合；E为无向图的边,连接四邻域或八邻域像素对。根据该无向图便可构建一颗最小生成树,其中边权为相邻像素颜色(R,G,B)的最大绝对差

(5)

式中Ij(p)为像素p在j通道的值。然后采用kruskal算法构建最小生成树。

对于该最小生成树中任意两点p,q,其路径是唯一的,因此,该路径长度也必然唯一,记为D(p,q),其值为路径上各边权重之和。基于此,可定义图像中任意两像素p和q的相似性

S(p,q)=S(q,p)=e-D(p,q)/σ

(6)

式中σ为参数用来调节该相似性。最终聚合代价为

(7)

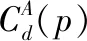
1.3 自适应选取参数

根据1.2节描述,非局部算法采用式(6)描述相邻两像素相似度,通过调节参数σ来权衡邻近像素对聚合代价的贡献大小：σ越大,S(p,q)则越小,聚合代价主要由最小生成树上邻近像素贡献,即聚合代价由少部分像素主导,导致算法在低纹理区域易出现错误匹配；反之,σ越小,将有更多的像素贡献代价,导致在高纹理区域误匹配率较高。

可以看出,σ的选择对最终视差精度会产生较大影响,目前的非局部立体匹配算法[10～12]多着重于最小生成树的构造,以期得到最符合图像结构的最小生成树,而对于σ多采用经验值。本文算法对参考图进行分析,自适应的选择合适的σ值。

首先将图像转至HSV颜色空间。在HSV空间中,像素的色度和亮度被分开,计算相邻像素的色度差为

(8)

式中h(p),s(p)分别为像素p的色相值及饱和度值,其中,色相和饱和度都经过了归一化处理。统计所有相邻像素色度差,便可求得图像平均色度差η

(9)

式中E为连接任意两相邻像素的边集。

根据平均色度差定义可知：η越大,图像颜色纹理则越丰富,为了降低误匹配率,在代价聚合时,邻近像素应做主要贡献,即σ越大；反之,图像纹理越单一,则需要更多像素参与主要贡献。可建立η与σ关系

σ=kη

(10)

式中k为比例系数。依据原图平均色度差η为不同纹理图像自适应地选择合适的σ。

1.4 视差选择及修正

视差选择采用WTA(Winner-Takes-ALL)策略

(11)

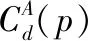
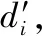
(12)

重新计算匹配代价

(13)

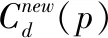
2 实验结果与分析

本文算法使用Middlebury2.0立体匹配评测平台提供的31组图像对进行实验。实验环境为：Visual Studio 2013下C/C++编译环境,Win10 x64系统,Intel Core i7—6700 CPU—3.4G Hz,16 G内存。

为验证算法实际性能,除非特别说明,否则本文中涉及到的视差图都未经过任何视差修正或后处理操作；实验中误差限为1像素。

2.1 匹配代价验证

为验证改进后代价的有效性,对代价改进前后非局部算法得到的视差图进行对比。图1(a)和(e)为原图；(b)和(f)改进前；(c)和(g)经过代价融合后；(d)和(h)经过对数变换后,改进后视差图中误匹配标记点明显少于改进前,尤其是低纹理区域。对比图(b)，(c)以及图(f),(g)可看出,融入垂直方向梯度代价后,算法在低纹理区域表现得到很大提升；对比(c)，(d)以及(g)，(h)发现,通过对融合代价作对数变换,能够进一步增强算法在低纹理区域表现。

图1 代价改进前后非局部算法对Wood1和对Rocks1图像处理获得的视差

如图2,通过比较代价改进前后非局部算法在Middlebury平台上31组图像对的平均误匹配率可知,融入垂直方向梯度代价后,算法的误匹配率大幅降低,再对融合代价作对数变换,可进一步降低算法误匹配率。

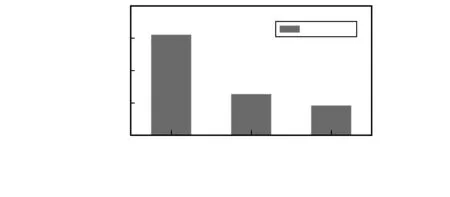
图2 代价改进前后非局部算法在非遮挡区域误匹配率

2.2 自适应参数分析

为验证平均色度差η与参数σ之间比例关系,分别计算不同纹理图像平均色度差,并运行改进代价后的非局部算法,得到各图像最佳σ值。

如图3所示,不同参考图具有不同的最佳σ值,且其变化趋势与平均色度差的变化基本一致；对比图3(a)和图3(b)可知,低纹理图像具有更小的η以及σ,这是因为在以式(5)为边权建立的最小生成树上,相邻像素点此时具有相似的视差值,较小的σ能够促使更多的像素参与聚合,提高匹配精度。可以看出,平均色度差确实能够反映图像纹理信息。

图3 不同参考图的平均色度差η及最佳σ值

通过改变k,可以改变η和σ的比例关系：

如图4所示,随着k值的增加,所提算法在非遮挡区域对Middlebury测试平台31组图像对的误匹配率有一先减再增的过程,并在k为1.0时取得最小值。

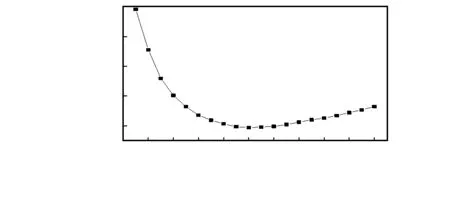
图4 不同k取值下的误匹配率

2.3 算法对比

为测试所提算法的总体性能,本文选取MST[9],ST[10],CS-GF[13]作为对照算法。实验中,涉及到的参数设置：α为0.15,β为0.48,τAD为9,τGRDX为0.5,τGRDY为0.5,k为1.0。

所提算法在Middlebury上31组立体图像对性能评估(无视差修正,误差限为1像素)的平均误匹配率最低,仅为7.86 %,精度最高；平均排名为1.61,其中在18组图像对中取得最好结果,在10组图像对中取得第二好结果,表明所提算法具有更好的泛化能力；本文算法运行时间为1.2 s,这是因为引入了垂直方向梯度以及对数变换,增加了计算量,导致处理时间增加。然而所提算法在小幅增加运行时间基础上,在精度及泛化性上有很大的提升。

表1为经过视差修正后,4种算法在本文实验环境中对Middlebury 2.0上31组立体图像对的评测结果。可以看出,经视差修正处理,所有算法精度均有不同幅度提升,同时运行时间也相应增加；而本文所提算法无论在非遮挡区域误差还是全像素误差方面仍旧取得最好的结果。

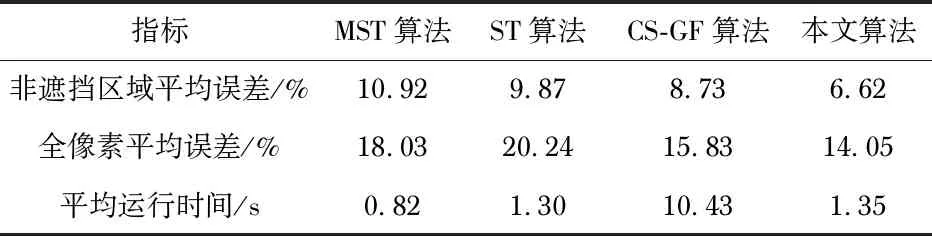
表1 不同立体匹配算法在Middlebury上31组立体图像对性能评估(经视差修正,误差限为1像素)

图5为各算法对Tsukuba,Teddy,Flowerpots,Monopoly图像对处理后得到视差。

图5 不同立体匹配算法在Tsukuba、Teddy、Flowerpots和Monopoly图像对上的测试结果

3 结 论

实验结果表明,所提算法在Middlebury测试平台上平均误匹配率为7.86 %,经视差修正后平均误匹配率为6.62%,匹配精度优于当前优秀的局部和非局部算法。