智能双车车距控制算法与优化策略*

张 丽， 周 峰， 张 涛

(河南理工大学 电气工程与自动化学院，河南 焦作454000)

0 引 言

高度智能化的无人驾驶技术，是智能汽车研究热点。为了推动无人驾驶技术的发展，在最新几届的智能车竞赛中，都提出了双车追逐系统的设计要求。竞赛中，要求智能车能自主根据路况及时调整双车速度及转向，在最短的时间内完成两车通过终点线，并且两车通过时间差较短者为最佳状态。

在双车追逐系统中，距离过近不利于后车的信号检测，距离过远时不能达到赛题的最佳要求。双车的速度控制是一个难点问题[1,2]，一方面双车的距离测定在运用中无法实时准确的测定，无法完全适应不同路径的距离测定，另一方面两车距离控制对象是一个非线性系统，无法准确对其进行建模。模糊控制算法具有不要求精确的数学模型,能够方便地将专家的经验与思考加入到知识模型中等优点,十分适合这种时变的、非线性的、高实时响应的系统[3]。

综上，为了解决双车追逐时车速与车距的最优问题，本文结合智能车双车追逐控制的特点，硬件设计上采用电磁导航方式[4]，通过超声波进行距离辅助标定，利用编码器进行路程积分，滤波[5]后通过无线发送方式将前车路程距离发送至后车，经过单片机处理后计算出双车的距离差。最后，通过模糊控制算法和增量式比例—积分—微分(proportion-integration differentiation,PID)[6]算法相结合对后车速度进行双闭环控制，从而使两车距离达到最佳状态。

1 双车车距控制算法设计

1.1 问题引出

本文以恩智浦公司在“全国大学生智能汽车竞赛”中指定的B型车模为研究对象。该车模参数为：车长74 cm,车宽25 cm,车高18 cm,车重约963 g，用电感检测赛道中的铜线电流大小为100 mA,频率为20 kHz，波形为方波的电流变化，舵机转向反应范围：左45°，右45°。本文提出的控制策略是基于双车在保持合适车距的前提下，完成动态实时追逐且顺利快速超车(即测距条件满足时进行超声波距离测定)。双车追逐示意如图1所示，距离M为双车追逐运动时前车与后车保持的动态距离。

图1 双车车追逐示意图

在双车比赛中，赛道类型多样且复杂，如有直道、直角弯、十字弯、小s弯等。目前，双车的测距已被广泛研究，大多测距方法分为摄像头测距、超声波测距、卫星测距、激光测距[7～9]等，这些测距方法在实际应用中，特别容易受环境影响而导致测量不精准。例如，在超车过程中，特别是当双车行驶在弯道时，由于受超声波测量角度的限制，会造成测量存在一定的误差。如果弯道处一般设有绿化带或其它遮挡时，双车车距的测量将会受到更大的限制。故本文采用超声波测距与速度实时积分相给合的方法测距，描述为：

1)双车发车前(直道，未运动)，采用超声波对双车之间的距离进行一次初始检测与标定，标定值记为Q，此时，M即为Q，为一固定值。

2)在双车追逐运动时，M是动态变化的，为了实时检测M的值，需对双车的速度各自进行积分，获得前车和后车已行驶的距离，记为L1(前车已行使距离),L2(后车已行驶距离)，同时将L1发给后车。

本系统中双车距离控制是建立在前车选定合适的车速(如中速、高速、超高速)前提下，后车进行实时追逐，运动中对前车进行PID闭环调节，使前车达到选定的目标速度，同时发前车行驶的距离给后车。后车在初始化成功后，一方面根据双车距离差对设定速度进行闭环调节，另一方面根据实时速度对检测速度进行PID闭环调节，使检测速度达到设计的目标速度。后车双闭环控制流程如图2所示。

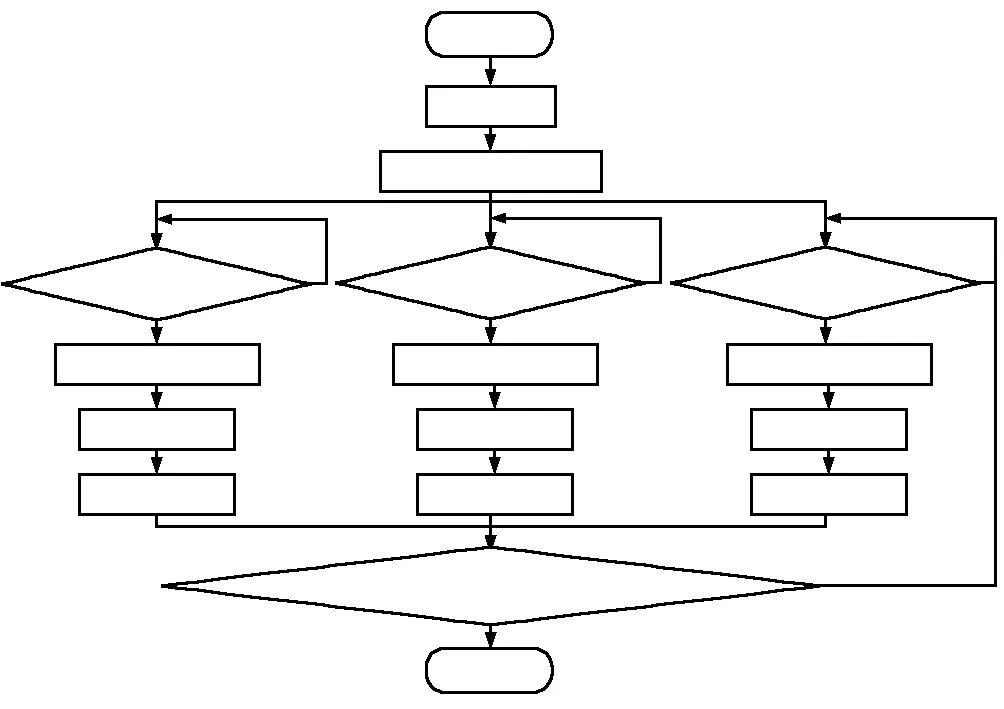
图2 后车程序流程

1.2 控制策略

在双车行驶过程中，为保证使后车很好地追逐前车，让两车始终保持在一个合适的距离，从而使双车能够以最短的时间完成比赛，获得更好的比赛成绩。本文提出了一种速度距离双闭环方法来实现车距控制，具体策略如下：

1)采用超声波测距与速度实时积分相给合的方法，实时检测双车追逐时的动态车距M(如图1中所示)。

2)对于前车，需要在起跑前设定其安全可靠的目标速度，本文采用增量式PID控制算法，得到当前速度的真实值，通过滤波后对当前速度进行积分，得到前车已走的距离L1。为了程序简便，可以通过对当前速度的连加，再除以由编码器齿轮数及电机齿轮确定的常数N，即∑Vo/N。

3)对于后车，需要先设置一个固定的目标距离S，通过将后车速度积分的积分值L2与前车已行驶的距离L1求差，再加上发车前通过超声波标定的初始距离Q，得到当前真实的路程差M=Q+L1-L2。后车控制流程如图3所示。本文通过设计模糊控制器得到当前的速度设定值Vi,再通过PID控制器调节以达到合适速度，保证双车以合适的距离进行实时追逐。

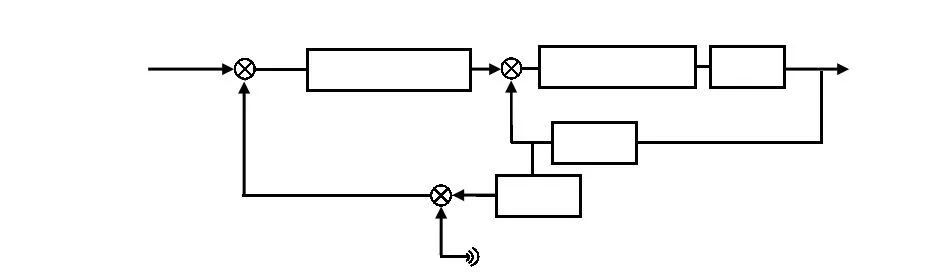
图3 后车控制流程

4)双车超车结束后，由于超车时后车行驶的路径受到赛道的影响，因此，需要对当前车距进行重新标定(采用超声波)，在检测到当前两车均为直道或满足超声波测距的要求情况下使用超声波对两车的距离进行重新测定。此时原先的后车变为前车，原先的前车变为后车，依旧按照前文提出的控制策略进行控制。

1.3 算法设计

1.3.1 模糊控制器设计

由于在双车追逐过程中无法准确对双车之间的距离模型进行建模，同时为了使不同的距离对应不同的速度输出，故本文采用参数可自行调节的模糊控制器，过程如下：

1)定义输入输出语言变量。距离调节的偏差即S-M作为偏差E,偏差E的变化率设为EC，后车速度的目标设定值Vi作为输出U。

2)定义偏差的论域E，偏差变化率的论域Ec,速度目标设定值的论域U。E=[-3,3],EC=[-6,6],U=[-4,4],对应域上E,Ec和U的隶属函数如图4所示。

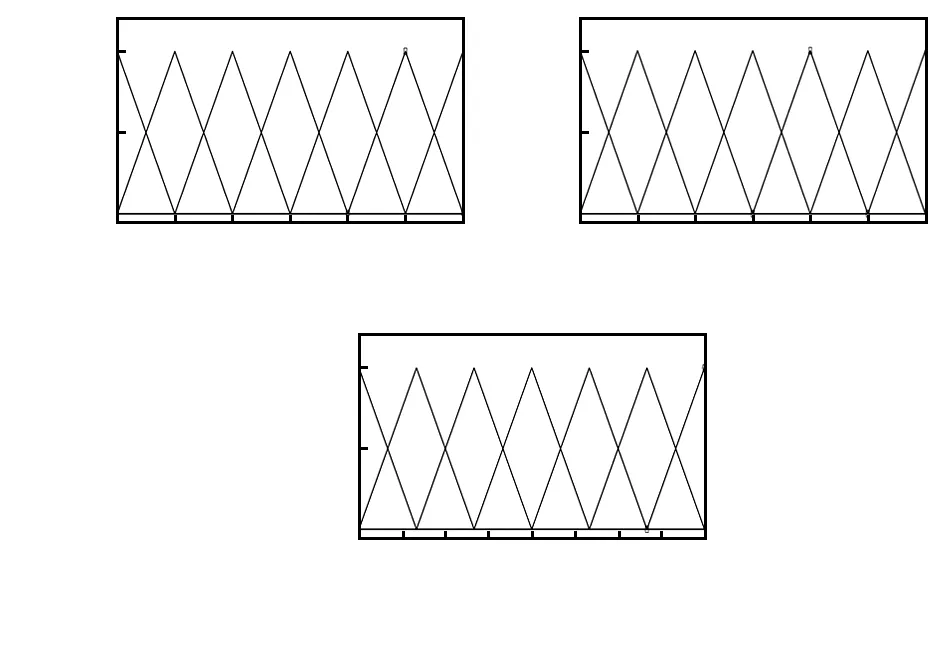
图4 E,Ec和U的隶属函数

3)依据专家系统规则，结合本文平时的调试经验，建立模糊规则表如表1所示。

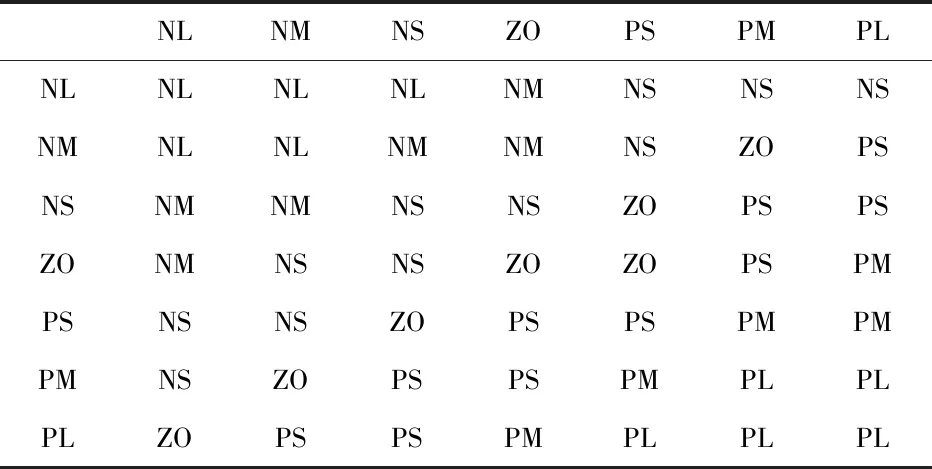
表1 模糊规则表

为了更加形象地描述本文设计的模糊规则表，将调试过后的模糊规则曲面拟合如图5所示，在模糊控制曲面中可以看出，距离偏差变化量与距离偏差变化率对应输出速度的变化曲线，例如当两车距离较大，距离变化量也较大时，模糊控制器输出较大的速度，当两车距离量较小，距离变化量也较小时输出较小的速度。

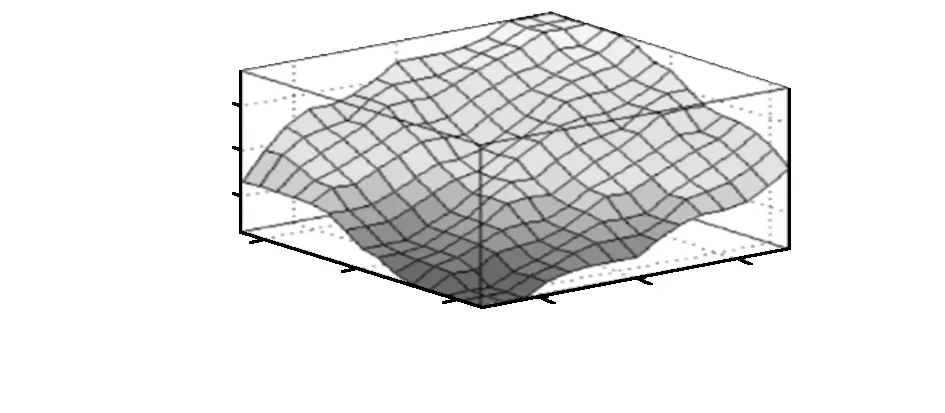
图5 模糊控制曲

1.3.2 双闭环PID算法

在距离的闭环控制中

Efuzzy=S-M=S-(Q+L1-L2)

(1)

Ecfuzzy=Efuzzyk-Efuzzyk+1

(2)

(3)

式中μ(|E|fuzzy,|Ec|fuzzy)为隶属度函数，Kv为不同状态下的加权。

在速度的闭环控制中,在得出当前速度设定值Vi后，采用增量式PID对当前值进行调节。设ΔVo[n]=Vo[n]-Vo[n-1]，则有

ΔVo[n]=Kp[e[n]-e[n-1]}+Kie[n]+

Kd{e[n]-2e[n-1]+e[n-2]}

(4)

式中e[n]=Vi[n]-Vo[n]。

2 仿真与实验

2.1 仿真测试

智能双车系统通过控制直流电机来达到控制速度的目的，本系统采用直流伺服电机控制，简化模型如图6(a)所示，其传递函数为

控制原理如图6(b)所示。

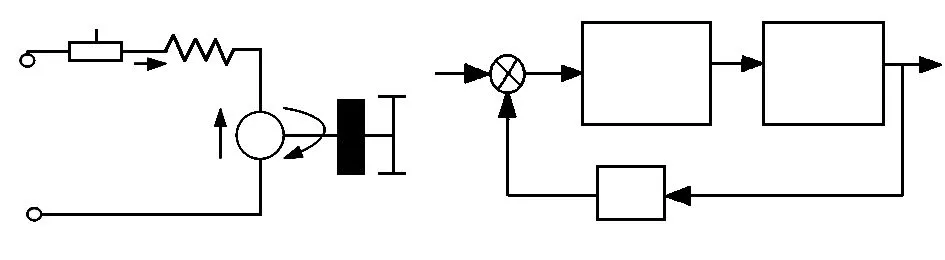
图6 直流电动机等效电路及电机控制原理

仿真时，在系统中输入阶跃信号，即模拟系统刚上电时的距离变化情况。仿真中，后车以前车为参照物，具体结果如图7所示。

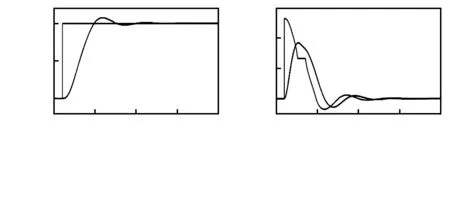
图7 距离与相对速度仿真

从仿真中看出:当输入阶跃信号时，输出的速度目标值超调量较小，且响应较快，说明该算法满足双车追逐系统设计要求，稳定性和适合性较强。

2.2 实际测试

实际测试环境如图8所示，赛道全长34.5 m。本文分别测试了两车在传统控制方式下和速度双闭环控制方式进行跟踪追逐的运行结果。在测试100组数据后，结果如表2、表3所示。

图8 实际赛道与双车追逐情况

控制方法碰撞次数速度 /(m·s-1)到达终点时间差/s传统控制0.81.981.02双闭环控制02.340.56

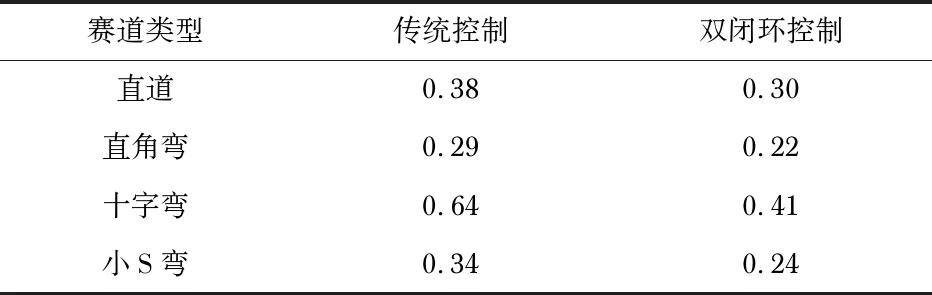
表3 不同类型赛道测试通过时间差实验结果 s

从实验数据可以看出，通过使用基于模糊控制的速度双闭环双车距离控制算法，比仅仅使用距离传感器来进行双车控制的方法，运行时间短，而且更加安全可靠，能够更加有效地适应各种不同的复杂赛道类型，对智能车控制的性能提升有着很大的作用。

3 结 论

1)本文所采用的距离速度双闭环控制方法，可以在弯道(U形弯度较小时)、十字赛道、坡道、以及环道处进行车距测量，该测距方法受周围环境的影响较小。

2)在实验中发现，双车的距离控制在直道上或弯道角度较小时两种方式区别较小，但在U型弯道角度较大时，测量车距存在一定的误差，双车的控制距离将会略受影响，加大了控制难度。

3)本文采用的速度距离双闭环策略，按照比赛的计时方式(时间=两车通过终点线的时间+两车通过终点线时间差×5)，最快速度达到2.14 m/s(2017年全国智能车大赛国一平均成绩为2 m/s)，大大提高了比赛成绩。

4)该算法也将有助于未来人类在无人驾驶领域中对双车甚至多辆车的有效控制。