形状记忆合金薄板低速冲击载荷下热力耦合行为分析
任旋畅,王 骏,2,许英杰,张卫红
(1.西北工业大学 机电学院,西安 710072;2.西北工业大学 无人系统技术研究院,西安 710072)
形状记忆合金(shape memory alloy,SMA)作为一种典型的智能材料,具有超弹性和形状记忆效应。相比于普通金属不超过0.5%的弹性应变,超弹性SMA最大可恢复应变通常可达5%~20%[1]。同时,SMA马氏体变体间相对较低的界面能可有效吸收振动和冲击能量,这种良好的阻尼特性使得SMA成为潜在的缓振和消声材料[2]。得益于其轻质、耐磨损、抗腐蚀、生物兼容性好等优异性能,SMA在航空航天、生物医学、交通运输、智能无人系统等领域得到广泛应用[3-6]。
针对SMA动态载荷作用下热力学行为的研究,多数致力于SMA材料变形、应力、相变和阻尼现象的描述。Hashemi等[7]采用Euler-Bernoulli理论对SMA悬臂梁和简支梁在正弦和脉冲载荷作用下的振动特性进行了分析,结果表明超弹性SMA具有良好的振动阻尼特性。邹广平等[8]采用SHPB实验装置研究了应变率对超弹性SMA动态性能的影响,在较高应变率下(102~104s-1),马氏体相变起始应力随着冲击次数逐渐增大,表现出逐次强化现象。超弹性SMA在循环加卸载时由马氏体和奥氏体相变导致的滞回环可吸收大量能量,将SMA嵌入复合结构中可抵消冲击和振动载荷引发的大应变能,从而减轻复合结构强载荷作用下的损伤破坏。Speicher等[9]通过使用NiTi合金来实现承重梁地震载荷后的重定位能力,并利用SMA超弹性大变形能力极大提高了缓震系统的韧性和延展性。Raghavan等[10]制备了纤维体积分数为20%的SMA纤维高聚物,增强后的聚合物材料拉伸和抗冲击性能显著提升。类似的SMA纤维增强方法使得复合材料抗损伤性和延展性也得到了极大改善[11-12]。
然而,上述研究集中在冲击或振动载荷作用下SMA杆、梁等结构的相变现象、应力波传播规律或阻尼特性,SMA薄板低速冲击载荷作用下热力耦合行为特征尚待进一步揭示。
本构模型是开展SMA热力学行为分析不可或缺的理论基础。近年来国内外众多学者在SMA本构建模方面开展了大量研究。Tanaka[13]、Liang等[14]和Brinson等[15]基于自由能驱动力理论建立了SMA本构模型,该类模型形式简洁,在初期得到了广泛应用。Bo等[16]和Lagoudas等[17]基于自由能与耗散势概念提出了可同时描述超弹性与形状记忆效应的SMA本构模型,该类模型可精确描述应力诱发下的正-反相变行为,但形式复杂计算量大,难以实现工程应用。Zaki等[18]通过引入内变量(马氏体体积分数、内应力张量、残余应变等)提出了一种三维唯象型本构模型,用以描述SMA热力学训练行为和双向形状记忆效应。该模型之后被Morin等[19]改进用以分析SMA的热力耦合行为、棘轮效应和功能性疲劳寿命。Chao等[20]提出了一种基于物理机制的超弹性SMA本构模型用以描述应变率相关的循环变形行为,模型给出了马氏体相变与奥氏体位错滑移之间的相互影响机制。Wang等[21]基于虚功原理、能量守恒和熵增原理,提出了一种考虑有限变形、热力耦合和循环载荷的多晶SMA本构模型,该模型精确描述了SMA复杂服役条件下残余应变累积、热力耦合效应、材料性能退化、相变光滑性转变等典型热力学特性。
本工作以Wang等[21]提出的SMA本构模型为理论基础,针对SMA薄板在不同冲击能量作用下的热力耦合行为进行实验研究,在显式有限元软件ABAQUS/Explicit中通过数值分析手段考察SMA低速冲击作用下马氏体相变、残余变形、冲击应力、温度演化等热力学现象,揭示低速冲击作用下热力耦合行为特征。
1 实验方法和材料
1.1 材料和试件
SMA薄板低速冲击实验样件尺寸及夹具设计参照标准ASTM D7136/D7136M—2012,试件尺寸为150 mm × 100 mm × 1 mm。冲击实验前,对试件进行热处理(500 ℃保温1 h后自然冷却)以保证常温状态下SMA超弹性。所有冲击实验样品用SiC砂纸抛光,除去表面颗粒确保试件表面粗糙度一致。试件的相变温度由差示扫描量热法(DSC)测量。
1.2 冲击实验系统
低速冲击实验在INSTRON-CEAST 9340型落锤冲击系统上进行,冲击过程中SMA薄板上温度变化由热成像仪记录,最高FPS为115,设备见图1。实验温度为室温,冲击实验分为4组,在配重2.5 kg条件下通过改变冲头下落高度来控制冲击能量,4组冲击能量分别为10 J、15 J、20 J、25 J。
冲击过程中原始采集数据为力-时间曲线,位移数据由如下数值积分公式对时间节点i处的力进行积分得到:
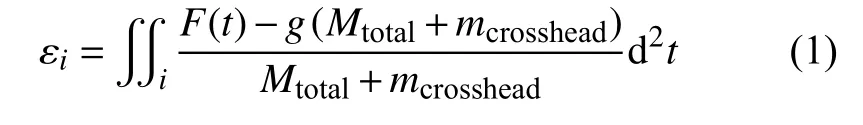
式中:g为重力加速度; Mtotal和 mcrosshead为冲击杆的质量和配重质量;t为在i时间节点处冲击所用的总时间; F(t) 为 冲击力;εi为i节点处的位移。在低速冲击过程中,冲头刚度足够大,其变形可以忽略,因此试样表面上的变形区域的深度等于冲头的位移。

图1 冲击实验设备 (a)CEAST 9340落锤冲击系统;(b)热成像仪SC7000Fig. 1 Impact test equipment (a)CEAST 9340 drop hammer impact system;(b)infrared camera SC7000
2 实验结果和讨论
2.1 DSC热分析结果
图2测量结果显示马氏体相转变开始温度Ms为-29.177 ℃,结束温度Mf为-57.117 ℃;R相转变开始温度Rs为11.667 ℃,结束温度Rf为-1.545 ℃;奥氏体相转变开始温度As为-4.031 ℃,结束温度Af为28.188 ℃[22]。由图2可知,经热处理后SMA常温条件下处于奥氏体状态,此时SMA在外力加载时展现出超弹性特性。
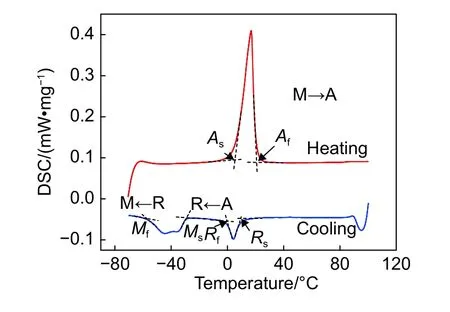
图2 差示扫描量热法下的SMA热分析图Fig. 2 Phase transformation temperatures of SMA measured
2.2 冲击过程中的力学现象
冲击载荷强度高、作用时间短,被冲击物体内部应力场变化剧烈、极易引发材料的损伤破坏。SMA材料兼具高强度、高硬度、高阻尼的特性,较普通金属来说其抗冲击性能更好,是制备抗冲击防护装甲的绝佳材料。
通常,室温条件下处于奥氏体状态的SMA薄板在经受冲击载荷作用时能够产生大的变形并耗散一部分机械能。实验中选取不同冲击能量,观测SMA薄板的冲击保护行为受冲击能量的影响。
图3给出了SMA薄板低速冲击实验中力传感器采集到的4组冲击能量下冲击力-时间曲线,整个冲击过程持续大约6 ms。冲击过程前半段,冲击力从初始零值急速增大并于3 ms时达到最大值,曲线上的波动源自应力波传播效应,此时薄板上冲击点附近SMA材料从奥氏体状态转变为马氏体状态。冲击过程后半段,SMA薄板由最大变形位置返回原始状态,冲击力急速减小并返回零值,薄板上SMA材料由马氏体状态重回奥氏体状态。SMA试件冲击力-时间曲线表现出典型的韧性特征,冲击能量被试件通过相变变形均匀吸收。冲击力-时间曲线图表明,随着冲击能量增加,冲击力的最大值Fmax明显增大,冲击能量由小至大,冲击力峰值分别为5193 N、6622 N、7721 N、8716 N。
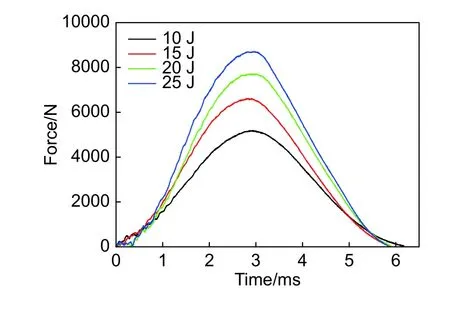
图3 不同冲击能量下的冲击力-时间曲线Fig. 3 Impact force-time curves under different impact energies
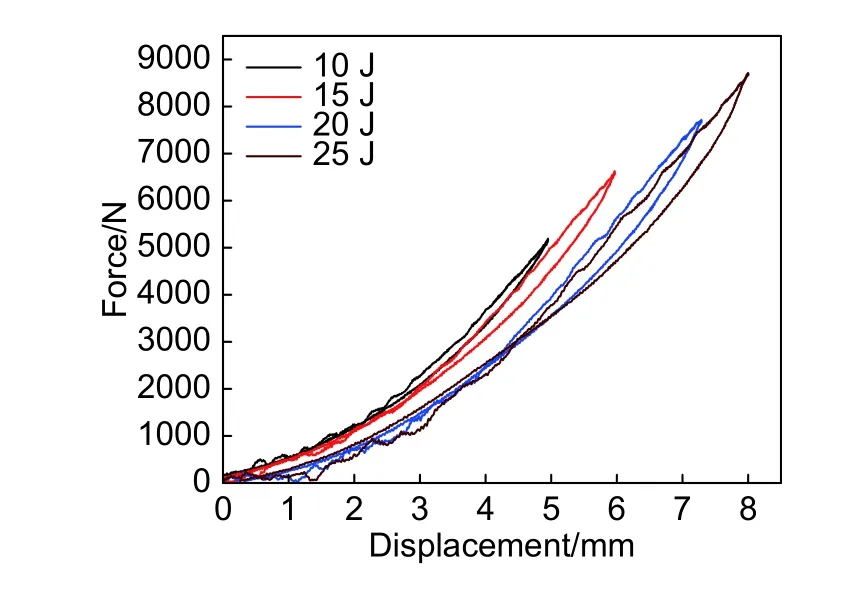
图4 不同冲击能量下的力-位移曲线Fig. 4 Force-displacement curves at different impact energies
图4给出了不同冲击能量下SMA薄板上冲击力-位移曲线。由图4可以看出,4条曲线分别构成近乎闭合的滞回环路,表明冲击过程中伴随有能量耗散现象。室温27 ℃条件下,SMA试件处于奥氏体状态,此时材料弹性模量和硬度较高。随着冲击力不断增大,薄板上冲击点附近SMA材料发生应力诱发的马氏体相变,引发相变变形。此时SMA弹性模量和硬度显著降低,导致冲头和SMA薄板试件之间的接触面积增加,分散了冲击应力的集中效应,降低了冲击点附近应力水平,这种特性可以有效减少塑性应变和冲击过程中材料表面的损坏。总体上来说,SMA薄板在低应力状态时发生弹性变形,当应力超过相变屈服极限后出现相变变形,同时相变过程中残余马氏体堆积和奥氏体位错滑移使得材料产生少量的残余变形,变形过程中具有明显的吸能特性[22]。
2.3 冲击过程的热现象
SMA薄板在冲击过程中,冲击点附近材料会发生马氏体相变,由此引发的相变潜热使得SMA薄板表面温度快速升高,此种独特的热力耦合效应可通过热成像图加以说明。图5给出了不同冲击能量下SMA薄板顶层的冲击瞬时热成像图,SMA薄板中心冲击前出现的圆形红色区域为保护冲头冲破试件的保护设计(下夹具上为保护冲头有圆形开孔),此区域属于环境因素,不影响结果置信度。实验数据表明升温过程约在3 ms内完成,热成像仪的镜头以115FPS难以捕捉到温度的最高点,但仍可以从瞬时图上看到最高温度位于变形最大的冲击点,温度分布以撞击点为中心呈圆形向外逐渐扩散。
图6给出了不同冲击能量下SMA薄板顶层冲击点温度变化,最高温度按冲击能量由小至大依次为42.87 ℃、44.66 ℃、45.67 ℃、46.93 ℃,不同冲击能量间温差值约为24~29 ℃。图中曲线波动主要是因为冲头短暂进入所选区域阻挡了一部分探测视野。不同冲击能量下的升温速率基本一致,至最高点后以较为缓慢的速率下降;在冲击过程中,由于SMA薄板热对流传导属性不随应力与温度而改变,不同冲击能量下表征出几乎一致的温度下降速率。
综上所述,低速冲击载荷下,SMA薄板随着应力的增加会产生相变变形,相变过程释放大量热量引发温度变化,而温度升高进一步影响SMA力学特性,如弹性模量、马氏体相变应力、硬化模量、最大可恢复应变等,展现出独特的热力耦合特性。
3 本构模型
SMA特有的超弹性、形状记忆效应等热力学特性本质上源自于温度或应力诱发的马氏体相变。Wang等[21,23-24]采用实验测试-理论建模-数值仿真相结合的研究手段,建立了一种考虑有限变形、热力耦合、马氏体重定向、残余变形、性能退化、光滑性转变等材料热力学特性的SMA本构模型。为清晰描述SMA薄板在低速冲击载荷下的相变、温变、应力-应变等热力学特性,本工作采用该本构模型来定义SMA材料属性。

图5 不同冲击能量下的冲击瞬时热力学响应 (a)10 J;(b)15 J;(c)20 J;(d)25 J ;(1)热成像图;(2)温度梯度直方图Fig. 5 Instantaneous thermodynamic response of impact under different impact energies (a)10 J;(b)15 J;(c)20 J;(d)25 J;(1)thermal image;(2)temperature gradient histogram
3.1 超弹性
超弹性现象是当环境温度处于奥氏体相变温度 Af之上时,应力作用下奥氏体与取向马氏体之间的相变过程。在有限变形热力学范畴内,SMA超弹性应力-应变关系由如下关系确定[21]:
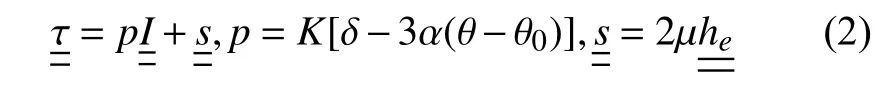
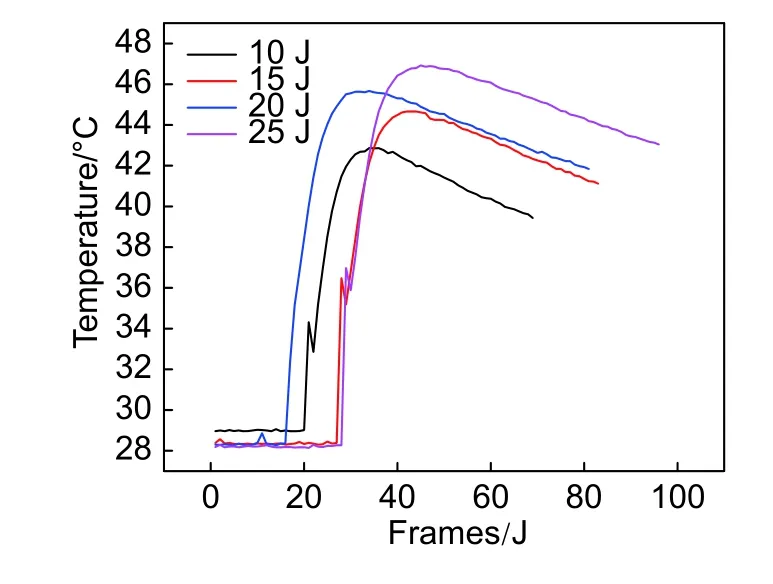
图6 不同冲击能量下的最大温度变化Fig. 6 Maximum temperature change at different impact energies
3.2 马氏体相变
马氏体相变是一种一阶非扩散固-固相变,具有高对称性的母相奥氏体在应力或者热载荷作用下转变为低对称结构的马氏体。这种低对称性使得马氏体具有24种变体,通常情况下马氏体变体具有两种聚集形式:孪晶马氏体和取向马氏体。孪晶马氏体中各种马氏体变体处于自协调状态,而取向马氏体中某种变体相对于其他变体处于绝对主导地位,此时材料在宏观上展现出取向特性带来的伪弹性应变,当应力状态发生改变时取向马氏体会依据应力状态发生重定向。马氏体相变和重定向过程的控制方程如下所示[24]:
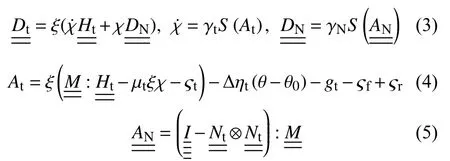
式中: At和分别为马氏体相变和重定向相关的热力学驱动力;χ 和 χ˙分别表示马氏体体积分数和其变化率,和分别是马氏体相变和重定向过程相关的变形率张量;是一个对称且无迹的Mandel应力张量;表示相变应变的方向;表示四阶单位张量;⊗表示张量积; γt和 γN分别表示相变和重定向过程相关的非负乘子; S(·)是一个标准化方程,用来提取热力学驱动力 At的符号和的张量方向;µt表 示相变应变的硬化模量; Δ ηt表示奥氏体与马氏体之间的熵差;ξ表示马氏体变体的饱和相变应变;ςt是 与单边约束相关的拉格朗日乘子; ςf和ςr是与双边约束相关的拉格朗日乘子0 ≤χ≤1; gt是一个正切硬化模量,用来描述相变过程的光滑性转变过程,具体形式如下:
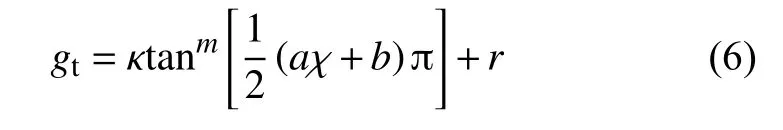
式中:π是圆周率,κ,m,a,b和r是控制光滑性转变过程的模型参数,加上 Δηt和 ξ两个模型参数,这7个模型参数遵循如下的演化方程:
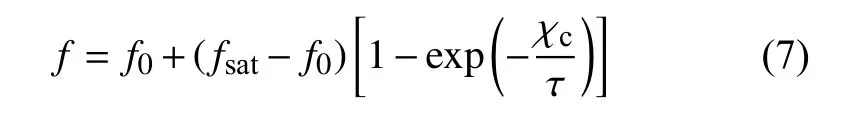
式 中: f∈{κ,m,a,b,r,Δηt,ξ}, f0和 fsat分 别 表 示SMA初始状态和稳定状态的材料性能参数;表示累积马氏体体积分数;τ表示无量纲的时间常数,上式用以描述SMA超弹性和耗散性能随周期循环加卸载退化现象。
3.3 残余变形
SMA在初始的数十次至数百次周期循环加卸载过程中材料性能表现出极强的不稳定性,最为突出的现象是残余变形的累积,这种现象可以在物理层面上归结为残余马氏体的堆积和位错滑移带的形成扩展。残余变形演化方程如下所示[24]:
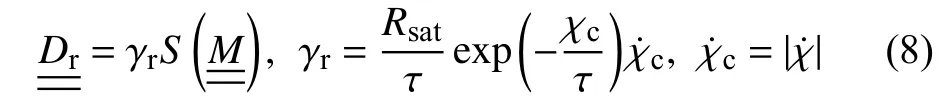
3.4 屈服条件
马氏体相变与重定向过程相关的屈服函数Ft和 FN形式如下[24]:
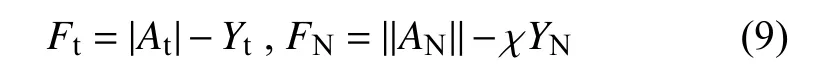
式中: Yt和 YN分别表示马氏体相变和重定向过程的初始屈服状态;屈服函数 Ft、 FN和相应的非负乘子γt,γN遵从如下的Kuhn-Tucker一致性条件:
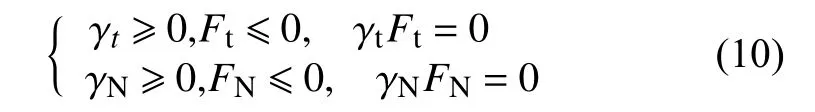
3.5 温度演化
由于固有耗散和相变潜热的存在,SMA相变过程伴随着大量的热量吸收或释放。基于吉布斯关系和能量守恒原理,可推导出如下的温度演化方程[21]:
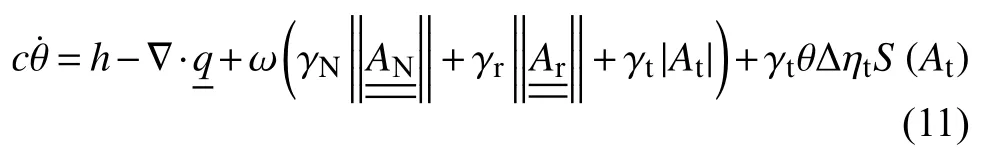
式中:c表示比热容;ω表示耗散能转化为热源的产热系数;h表示外部热源;表示热流密度,可由如下的傅里叶定律确定:

式中:k表示热传导系数。
4 仿真
借助有限元软件Abaqus/Explicit中自定义材料子程序模块VUMAT,可实现上述本构模型的数值开发和有限元集成。本工作中SMA薄板低速冲击仿真将采用基于上述本构模型所开发的用户自定义SMA材料,着重分析SMA薄板在冲击载荷作用下温度场和变形场,并对仿真结果与实验数据进行对比。
4.1 有限元几何模型
SMA薄板低速冲击有限元仿真中,冲头和SMA薄板有限元模型与冲击实验保持一致。冲头为直径20 mm的“子弹”式冲头,以90°的方向垂直冲击SMA薄板,冲头与SMA薄板间接触算法选用罚函数法,接触位置为冲头与SMA薄板表面相切的临界位置。仿真过程中冲头采用解析刚体,薄板选用八节点六面体线性实体减缩积分单元C3D8RT进行网格划分,该单元可以适用于冲击过程中复杂的热力耦合问题的求解计算,且对网格扭曲敏感性低,使其能够更好地模拟材料的大变形现象。整体有限元模型如图7所示,薄板的中心受撞击区域进行网格细化。

图7 薄板件有限元单元划分示意图Fig. 7 Schematic diagram of finite element unit division of sheet part
4.2 材料及边界条件
计算采用的热物性参数为:SMA比热500 J/( kg·K ),导热系数18 W/(m·K),塑性功转化为热的比率为0.8,马氏体及奥氏体的相关力学参数见表1。SMA薄板上初始温度定义为28 ℃,由于冲击过程全程仅历时6 ms,故不考虑对流和辐射热边界条件。如图8所示,有限元仿真过程中边界与载荷条件与实验过程保持一致,SMA薄板长边约束三个方向的自由度,解析刚体定义预设初速度,冲击能量设定为20 J。
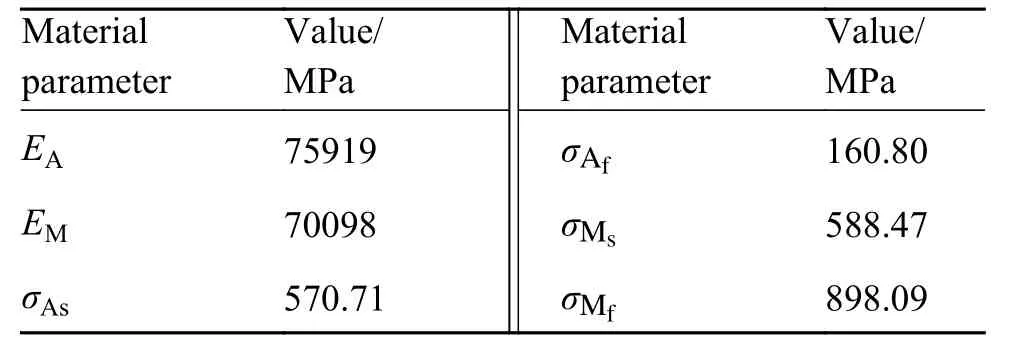
表1 SMA薄板的力学参数Table 1 Mechanical parameters of SMA sheet
4.3 数据分析
由于SMA的相变是热-力耦合过程,潜热和固有耗散决定了相变期间的吸放热,在环境温度不变的情况下,外力加卸载可引发相变并导致温度变化。图9给出了冲击过程最大变形瞬时SMA薄板背面应力、温度、位移及马氏体体积分数云图。从图9可以看出,温度场分布状态与实验相近,主要集中在冲头撞击点附近,由于冲击过程的瞬时性,温度响应尚未发生扩散。同时鉴于相变潜热是SMA在冲击载荷下温度变化的主要原因,马氏体体积分数云图与温度场云图类似。由此可知,对仿真过程中马氏体体积分数的监控可对SMA构件的温度场变化做出预测。
图10为冲击力-时间曲线的仿真结果和实验数据对比,由图10可以看出,仿真结果和实验数据整体趋势吻合,数值误差在3.7%以内。对比结果验证了数值仿真方法的有效性。
图11为位移-时间曲线的仿真结果和实验数据对比图,由图11可以看出,仿真结果和实验数据整体上位移变化趋势吻合,数值误差在7.5%以内。仿真结果中位移早于实验数据达到最大值,0.0055 s处位移上升表示冲头离开,薄板向上振荡,此处SMA薄板由于相变过程中马氏体堆积和奥氏体位错滑移展现出0.5 mm左右的残余变形。
图12为撞击点温度变化的仿真结果和实验数据对比图。由图12可以看出,仿真结果和实验数据整体吻合较好,最大误差在0.4%左右。此处温度变化主要来源于相变潜热,马氏体体积分数会随着应力升高而逐渐增加。
图13给出了冲击实验中难以测定的马氏体体积分数分布云图。冲击过程中,随着冲击力的增大,马氏体体积分数逐步上升且马氏体相变区域扩张;当冲击力回落时,马氏体发生逆相变重回奥氏体状态,最终薄板上马氏体体积分数全部归零。

图8 薄板所设置边界条件 (a)俯视图;(b)侧视图Fig. 8 Boundary conditions for the sheet (a) top view;(b) side view

图9 仿真过程中SMA薄板背部场状态 (a)Von-Mises应力云图;(b)温度场云图;(c)位移场云图;(d)马氏体体积分数云图Fig. 9 Field state of SMA sheet during simulation (a) Von-Mises stress cloud map;(b) temperature field cloud map;(c) displacement field cloud map;(d) martensite volume fraction cloud map
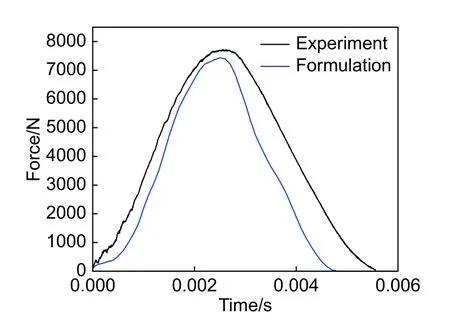
图10 仿真与实验力的结果对比Fig. 10 Results comparison between simulation and test force
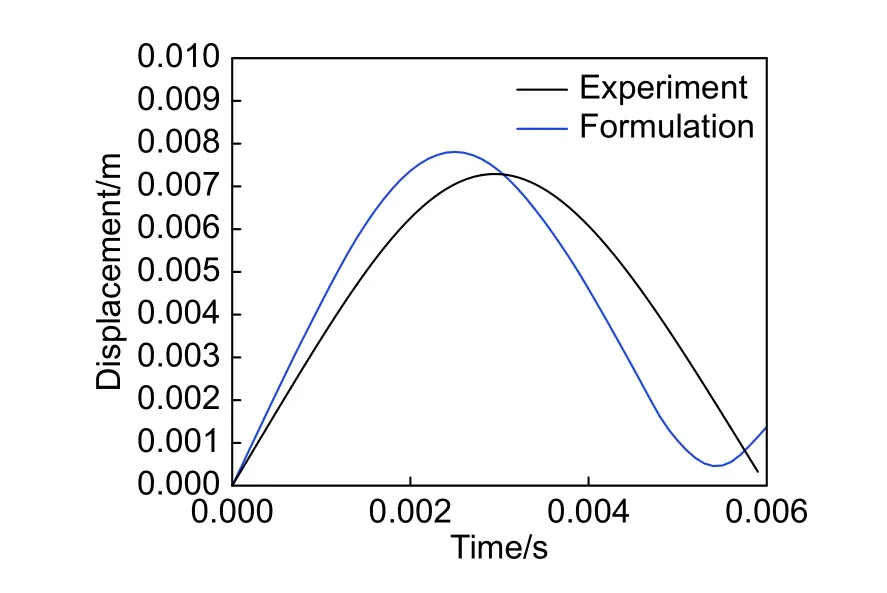
图11 仿真与实验过程位移对比Fig. 11 Comparison of displacements results between simulation and test process
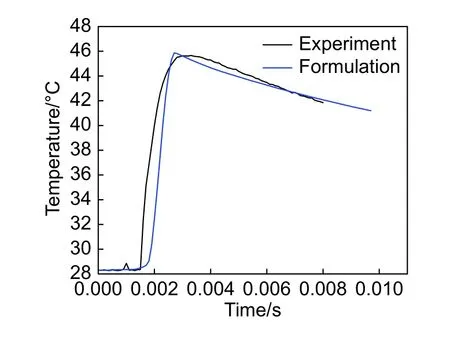
图12 仿真与实验过程温度对比Fig. 12 Temperature comparison between simulation and test process
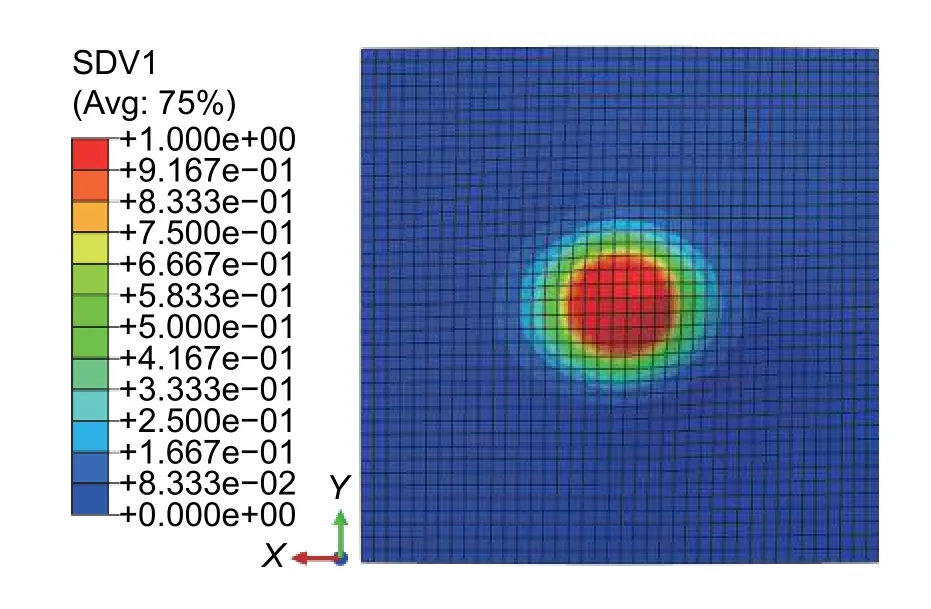
图13 冲击过程中马氏体体积分数局部放大图Fig. 13 Local enlarged view of martensite volume fraction during impact
5 结论
(1)SMA薄板低速冲击实验结果表明,本实验所选取SMA试件在实验过程中表征出了超弹性,滞回曲线揭露出的较小残余变形符合超弹性性质。显著的温度场变化表明SMA薄板在冲击过程中伴随有马氏体-奥氏体相变潜热的产生,使得SMA具有独特的热力耦合特性,并使其在冲击点附近温度升高24~29 ℃左右之后又回落到室温,过程较为短暂,持续6 ms左右。
(2)SMA薄板低速冲击实验有限元仿真,应力场分析结果表明,在20 J冲击过程中,大部分区域应力值低于747 MPa,四周边界处应力仅为300 MPa左右。相比于应力场,温度场变化较为集中且分布更加均匀,升温现象主要出现在撞击点四周呈环形分布,与实验情况一致。
(3)通过对比,SMA薄板上温度场、变形场演化规律仿真和实验基本保持一致,数值基本吻合且误差在10%以内,验证了仿真模型的正确性。

