基于THAFTS软件考虑地形影响的浮式平台水弹性响应
陆 晔,周 叶,范垂中,张正伟,田 超
(1.中国船舶科学研究中心,江苏 无锡214082;2.大连船舶重工集团海洋工程有限公司,辽宁 大连116113)
0 引言
众所周知,海洋浮式结构物使用安全性的最关键因素是设计所依据的环境条件与载荷的合理程度,而合理地预估在“复杂多变”环境中“漂泊不定”的浮体结构所承受的载荷,几乎是科技工程界面临的“永恒挑战”。与外海开阔海域的情形不同,浮式平台在岛礁附近布置处将永远面临复杂的海底地形。目前常用的商用软件SESAM、AQWA 等仅能计算均匀水深状态下浮式平台的运动和载荷响应,而不能考虑近岛礁实际的复杂地形环境,而这种地形起伏导致水深变化的复杂因素在浮式平台运动和载荷响应评估中起到了至关重要的作用,这是平台波浪载荷预报和结构安全性评估中必需考虑的实际问题。
自吴有生[1]提出三维线性水弹性力学理论以来,在无限水深和均匀水深的情况下评估浮体的水弹性响应已然成熟,而考虑非均匀地形对水弹性响应的影响,也引起了越来越多学者的关注。Dewi 等[2]分析了一个长150 m,半径4 m 的半圆柱薄板,布置在平均水深6 m 处对入射波的影响。Athanassoulis等[3]、Belibassakis 等[4]和Gerostathis 等[5]研究了不平海底浅水条件下的小波幅波浪特性,结合二维的弹性薄板进行了水弹性分析。Andrianov 等[6]分别计算了二维超大型浮体在无限水深、有限水深和浅水下的波长、波向等多种参数对水弹性响应的影响。孙辉等[7]、吕海宁等[8]和宋皓等[9]通过在水池底部分别放置两个不同弦长的圆柱形沙丘和一个三维的椭圆形沙丘来模拟不平坦的海底地形,开展了考虑海底地形影响的超大型浮体在规则波和不规则波下运动模型试验。Kyoung 等[10]考虑了四种不同海底形式来研究对箱式超大型浮体的水弹性影响。Lin[11]计算比较了超大型浮体在均匀水深和变水深条件下的波幅变化。Buchner[12]研究了平直斜波的海底地形对船舶运动的影响,还讨论了斜坡的边界应采用斜坡处理而非直壁截断的合理性。Ferreira 等[13]在Buchner 的模型基础上增加了几种地形处理方式,再次证明了海底地形采用斜坡处理的必要性。Hauteclocque 等[14]同样假设海底地形为第二个分析物体,针对海底斜坡进行光滑处理,从而较为准确地预报LNG 船的耐波性。Utsunomiya 等[15]分别计算了均匀海底、1/75 斜坡和不均匀海底的箱式超大型浮体水弹性响应。Pinkster[16]提出了一种简化的方法,适用于码头附近系泊停靠多艘船舶时,可以划成多个区域进行单斜波海底地形边界的水动力计算。
泻湖内外岛礁旁,海底条件为变水深,针对该特有的环境条件,Wu[17]和田超等[18-19]系统地阐述了计及波流不均匀性、变水深海底条件及多模块流固耦合效应的岛礁海域超大型浮体三维线性水弹性力学理论与三类数值分析方法,通过在“神威·太湖之光”超级计算机上应用的快速计算并行程序与模型试验结果进行了验证。第一类方法的本质是针对泻湖中间海底较平坦海域,假定可直接采用现有的开阔海域定水深船舶三维水弹性力学数值方法求解布设在该区域的浮体响应。杨鹏等[20-21]采用第一类方法对比分析了均匀水深和近岛礁环境条件下三模块超大型浮体的运动响应,并指出考虑复杂的海底地形计算得到的设计载荷对于结构评估是偏安全的。本文也将基于缓变水深条件的浮式结构物水弹性力学分析方法,将海底地形作为固定边界条件,分析近岛礁复杂地形条件情况下的浮式平台运动响应规律。
1 近岛礁浮体水弹性力学分析方法
1.1 水弹性力学方程
假设浮体周围流体是均匀的,无旋且不可压缩,则浮体的水弹性方程可表示为:

式中:{p}= {p1(t),p2(t),…,pm(t)},[A]、[B]和[C]分别是附加质量矩阵、附加阻尼矩阵和恢复力矩阵,为广义波浪力矩阵。
1.2 复杂海底地形下的边界条件
当浮式平台部署在岛礁旁,此时可将复杂海底地形作为固定边界,考虑其对浮体绕射和辐射的影响。则浮体绕射势满足的海底边界条件变为:
海底条件[B]:
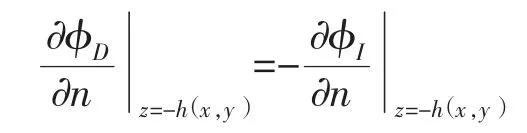
绕射势的定常部分φD采用格林函数法求解:

式中:Q 为源点,P 为场点,S0为物面,SB为海底,σ(Q)为物面和海底上的源强,G(P,Q)为有限水深脉动源格林函数。绕射势的物面和海底上的源强σ(Q)可以分别应用物面和海底边界条件求取:

辐射势的求解与绕射势类似,只是将物面和海底边界条件分别替换为:
物面条件[S]:
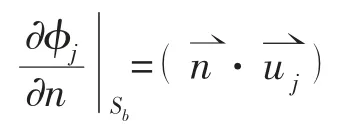
海底条件[B]:

辐射势的定常部分φj的求解同样采用格林函数法:

当考虑复杂地形时,海底地形是非常错综复杂的,仅仅考虑均匀水深不能完整地表达海底地形起伏对波浪产生的扰动,因此这里的底部条件需要改成非均匀海底条件,且法向不可穿透,在现有THAFTS水弹性分析软件上实现了考虑缓变平坦地形影响的功能,为近岛礁复杂环境条件下浮体的水弹性响应初步分析提供了一种快速评估方法。
1.3 多参数并行化快速计算方法
近岛礁浮式结构物除了形状复杂外,所处环境为非均匀海底浅水环境,因此,需要用到大量的面元数去离散浮式结构和非均匀海底。较大的面元数意味着所获得的影响系数矩阵为一个阶数巨大的非对称复系数稠密矩阵,此外,较多的波浪频率和模态数都导致了庞大的计算量,分析过程十分缓慢。根据现有水弹性力学分析程序,针对多级并行编程模型的并行算法设计与高效实现,通过湿面元、波浪频率等各级向量层的多极并行,在目前运算速度世界TOP500 排名第一的“神威·太湖之光”超级计算机上的应用,可实现近岛礁非均匀海底条件下浮体与波浪的相对运动预报及结构动响应预报的三维线性水弹性力学快速计算。
2 浮式平台水弹性响应
2.1 平台主要参数
浮式平台主要参数见表1。由于平台布置的位置水深较浅,且海底地形起伏不定,因此不得不考虑非均匀地形对浮体的载荷影响。为了减少不必要的过多的计算量,仅选取能影响浮体运动和响应的局部地形范围,即长200 m,宽120 m,地形的长度和宽度方向与浮体一致,使浮体于水面的投影恰在地形水面投影的中央;地形完全浸没于水面以下,边缘采用斜面平滑过渡到39 m 水深,海底其他地方为40.5 m 均匀水深,在平台布置点处水深约30 m。其中浮体水动力网格为3 476 个,地形水动力网格为9 792 个,整个带复杂海底地形模型水动力网格为13 268 个。图1给出了浮式平台相应的水动力模型和带复杂地形的水动力模型。
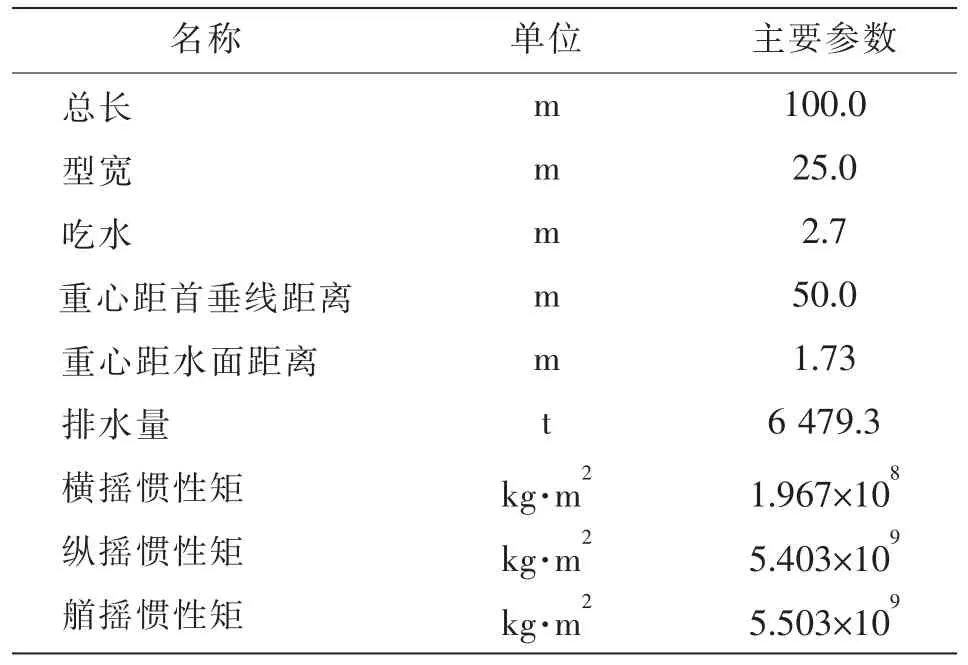
表1 浮式平台主要参数Tab.1 Principal particulars of the floating platform

图1 浮式平台及带地形的水动力网格Fig.1 The hydrodynamic panels of the floating platform with the seabed
2.2 地形影响

图2 浮式平台两种水深条件考虑地形的附加质量Fig.2 The added mass of the floating platform under two kinds of water depth with seabed
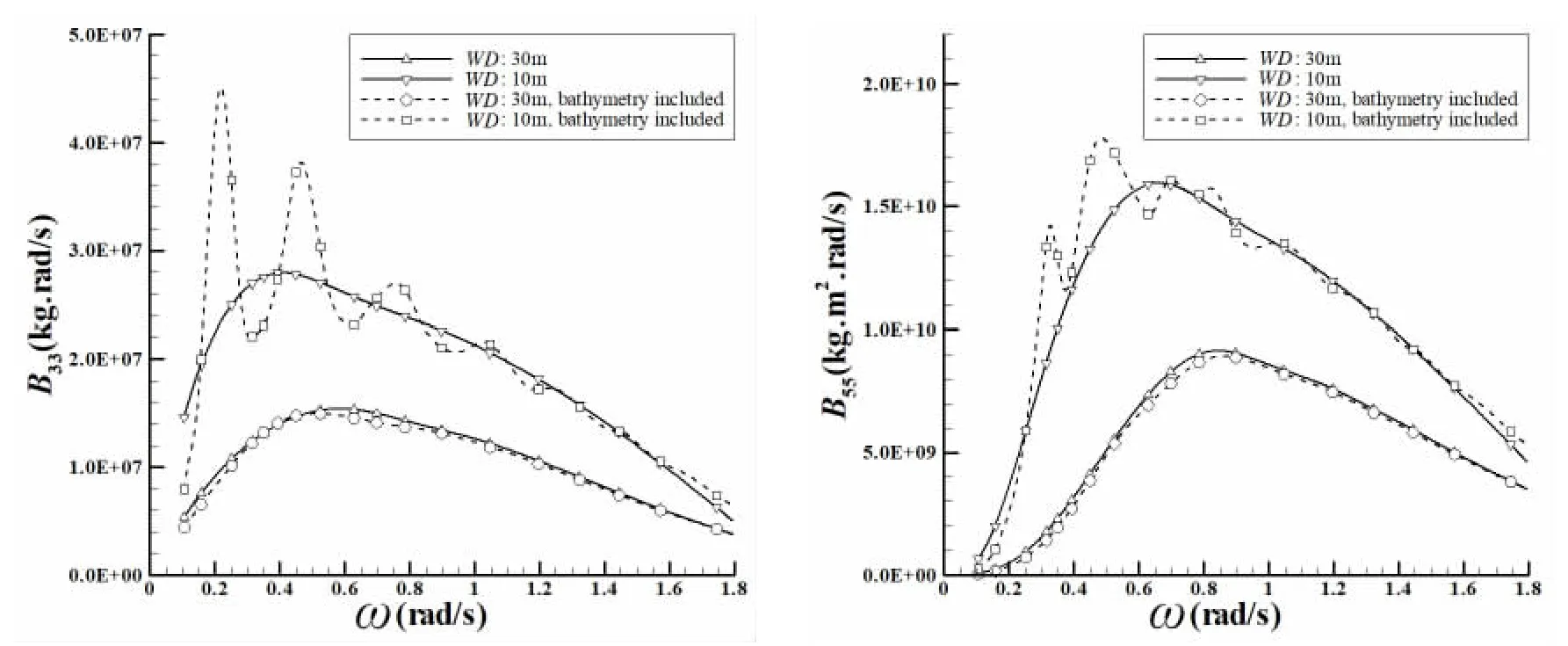
图3 浮式平台两种水深条件考虑地形的附加阻尼Fig.3 The damping of the floating platform under two kinds of water depth with seabed

图4 浮式平台两种水深条件考虑地形的波浪激励力(0°)Fig.4 The exiting forces of the floating platform under two kinds of water depth with seabed in follow sea
图2~6给出了30 m、10 m 均匀水深及带有复杂地形情况下,浮式平台的附加质量和附加阻尼,0°波浪激励力和运动响应以及载荷传递函数比较。
由图可知,与水深变化的影响不同,带有地形计算的浮体附加质量和附加阻尼都是围绕均匀水深曲线做振荡,而10 m 带地形的振荡幅度要比30 m 带地形的大。在0°浪向角下的波浪激励力和运动响应,30 m 带地形与30 m 均匀水深的计算结果差异不大,而10 m 带地形与10 m 均匀水深的变化比较明显,尤其体现在低频区域的高幅振荡。
0°浪向角均匀水深下的中横剖面垂向弯矩传递函数均为随着水深的变浅,峰值变大,峰值频率变小,而带地形的中横剖面垂向弯矩传递函数变化则不同,30 m 带地形比30 m 均匀水深计算的中横剖面垂向弯矩传递函数幅值要小,在高频段几乎重合;10 m 带地形比10 m 均匀水深计算的中横剖面垂向弯矩传递函数幅值要大很多,且峰值频率有所变小,同时振荡比较明显。另外,图7给出了30 m 带地形不同浪向角下平台中横剖面的垂向弯矩传递函数,图8给出了30 m 带地形不同浪向角下平台L/4 和3L/4 剖面垂向剪力传递函数。
2.3 短期极值预报及设计波参数
根据平台布置目标海域的海况实测资料,初步选定平台生存海况的波浪谱为适用于有限风区的Jonswap 谱:


表2 设计波参数Tab.2 The design wave parameters
浮式平台受多种外载荷作用,波浪载荷是该浮式结构物所受外载荷的主要部分,对总纵强度的校核起决定性的作用。本文采用设计波法对波浪载荷进行计算。
表2给出了该平台的设计波参数。根据不同浪向角下的载荷传递函数极值在0°和180°为最大,故取该两种角度进行计算。
2.4 应力分布
应用水弹性方法进行近岛礁浮式平台的应力分析,不需要像传统的方法那样基于载荷计算的结果,提取相应的外载荷再施加至结构模型上进行计算,而只需要在模态分析单位波幅的应力结果基础上叠加设计波参数,即可获得平台的应力分布结果。结果显示,在不考虑应力集中的情况下平台中部应力较大,L/4 剖面剪力短期预报极值设计波参数下平台等效应力最大,如图9所示。
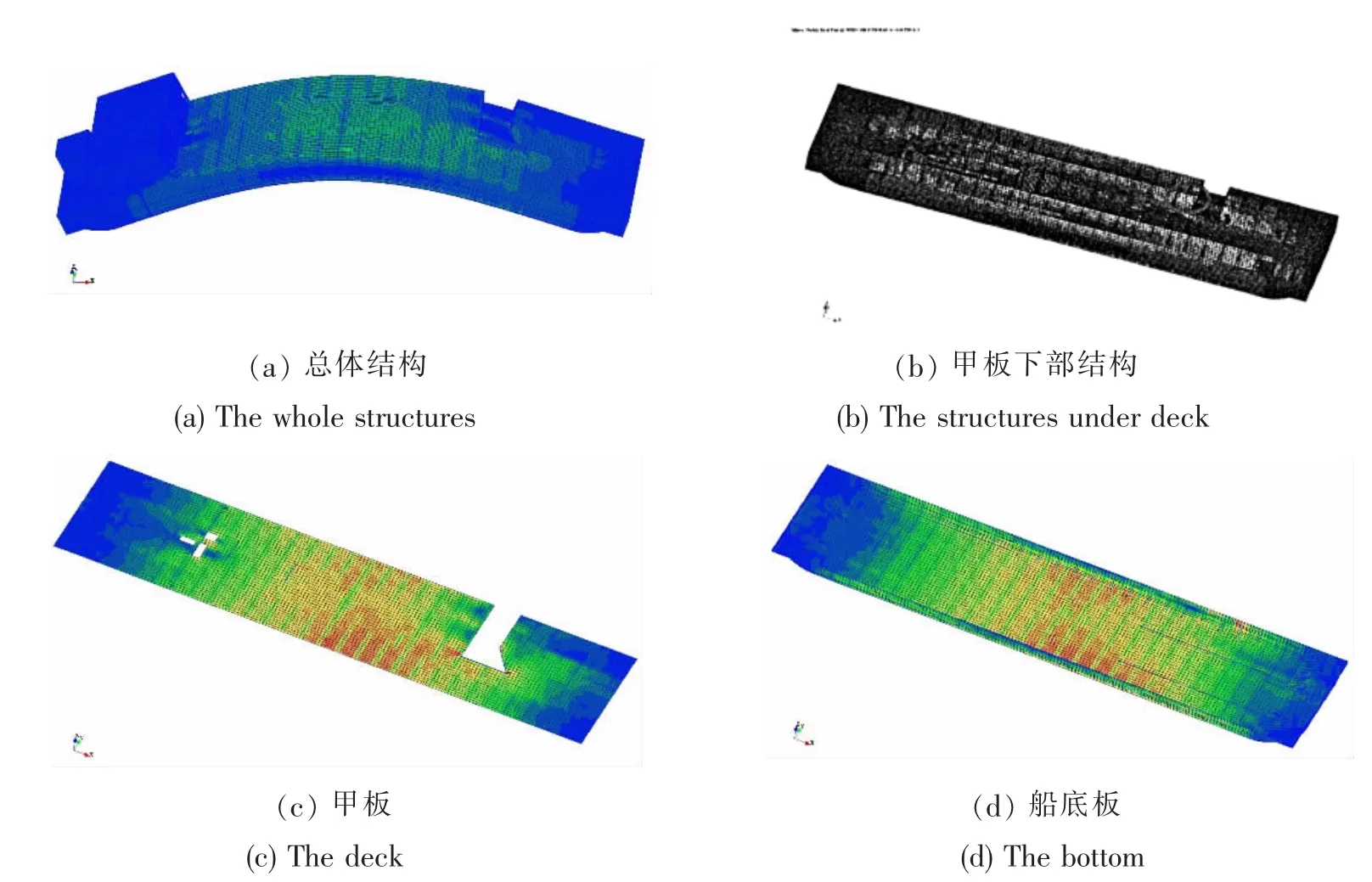
图9 近岛礁浮式平台结构应力分布Fig.9 The Von Mises stresses distribution of the floating platform
3 结论
本文针对近岛礁布置浮式平台中需要考虑复杂地形的热点问题,在三维线性水弹性的基础上采用了将固定海底地形作为边界条件的分析方法来处理非均匀海底地形对浮体的影响,文中基于THAFTS软件,通过模态叠加方法进行三维水弹性分析,对比了浮式平台在均匀水深及考虑复杂地形条件下的结构的运动和应力响应,验证了在近岛礁布置浮式平台必须考虑非均匀海底地形的影响的重要性。上述研究表明:岛礁存在及平台在岛礁周围的布置位置对平台运动和载荷响应的影响非常大,在对近岛礁浮式结构物的运动和载荷响应进行预报时,必须考虑岛礁及海底地形的影响。

