基于比例系数-有效独立法对圆柱壳声辐射预报的测点优化布置研究
余 鹏,陈美霞,谢 坤
(华中科技大学 船舶与海洋工程学院,武汉430074)
0 引言
圆柱壳结构作为潜艇的主要组成部分,对其振动响应及辐射声场的研究具有重要科学意义和实用价值。如何合理布置圆柱壳上的一系列传感器来对壳体的振动响应进行监测和预报,进而进行针对性的控制就显得非常重要。
目前针对圆柱壳结构的传感器优化布置,主要有两种方法:一是文献[1]中提出的均匀布置方法,即沿圆柱壳周向和轴向等间距地布置一系列测点,通过分析不同间距时得到的预报结果确定合适的测点布置方案。随后,大部分学者[2-4]均是采用的均匀测点布置方法,这种方法虽能得到准确的预报结果,但对测点数目要求较高,且在测点位置的选取上具有很大的盲目性和主观性;二是文献[5]中以模态矩阵的条件数为目标函数,采用逐步削减的方法确定测点布置方案。这种方法可有效地避免测点选取的不确定性,但对于频段较高时的振动响应预报,因其模态密集,很难得到准确的模态信息,从而对振动响应结果产生很大的误差。
Kammer[6]在对大型空间结构传感器优化布置研究中提出的有效独立法(effective independence,EI)是目前应用最广泛的方法之一。其基本思想是按照各待选测点对目标模态矩阵线性独立性贡献大小进行排序,以优化Fisher 信息矩阵,用迭代的方法逐步删除线性独立贡献量小的测点位置,直至达到指定的测点数。针对不同类型的结构,众多学者在有效独立法的基础上进行了不同的改进,如Meo[7]提出了用单位刚度的模态应变能作为驱动点残差系数的有效独立-驱动点残差法,杨雅勋[8]提出了以模态应变能反映目标矩阵最大线性无关性的能量系数-有效独立法等等。
对于本文中的圆柱壳结构,由于其振动模态的对称性及反对称性,此时对称和反对称位置,或间距较小的节点可能对模态矩阵线性独立性的贡献都很大,但是这两者往往提供的是重复的信息。若利用传统有效独立法,逐步删除对模态振型贡献小的候选测点,就不可避免地产生所选测点的信息冗余问题。基于此,本文用模态振型比例系数评价两测点间的信息独立程度,提出了一种能够同时满足所选测点模态可测性和避免信息冗余性的测点优化布置算法。
本文依据模态叠加原理,将水下结构的振速场在干模态空间中展开。利用比例系数-有效独立法得到的测点布置方案,与均匀布置方法[1]、基于条件数法[5]及传统有效独立法[6]得到的测点布置方案进行对比。结果表明,对于圆柱壳结构,比例系数-有效独立法更好地保留了结构的振动模态信息,且声振响应预报的精度更高,是一种更优的测点布置方法。
1 基本理论
1.1 模态叠加理论
对于水下弹性结构的振动响应,其运动方程为:

式中:M、C 和K 分别为结构的质量矩阵、 阻尼矩阵和刚度矩阵,p(t)为流体与结构交界面上由于结构振动引起的流体载荷,f(t)为除了p(t)以外的外界激励,x(t)为结构各节点位移向量。
经Laplace 变换后,得到结构频域中的振动表达式为:

根据模态叠加的原理[9],可将结构振速在干模态空间中进行展开:

式中:V 为结构各节点的速度矢量,φr为结构在空气中的第r 阶振型,qr为第r 阶模态坐标。
结构节点的速度矢量与位移矢量的关系如下:

由模态正交性,结合(2)-(4)式可得:
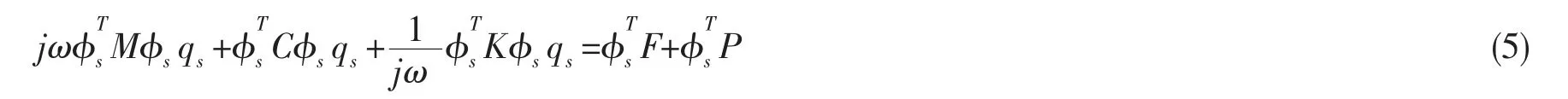
由此,可得第S 阶模态坐标为:

(6)式表明,将水下结构的振速在干模态空间中展开是合理的,将流体载荷作为外部激励力,流体载荷只对模态坐标有影响。
由(5)式可知,无阻尼结构在空气中自由振动的动力学方程为:

式中:ωr是结构在空气中的固有频率。对(7)式进行质量归一,即可得:

将上式代入(7)式,可得:

当结构在水中振动时,流体介质对结构振动的影响可以表示成附加质量的形式,则(7)式可变为:

式中:Δms是模态附连水质量,ωs是结构水中模态的固有频率。
结合(8)-(10)式,可得结构在空气和水中固有频率的换算公式如下:

(11)式表明,根据边界元离散得到的模态附连水质量,即可对结构在每阶振型下的空气和水中固有频率进行换算。
在中、低频段范围内,由于高阶模态对结构振动响应影响很小,所以可以采用模态截断的方法,忽略高阶模态的影响。根据振动响应分析的最高频率及固有频率的换算公式,可得结构在空气介质中进行模态分析的最高频率,从而得到模态截断阶数N。假设可选测点总数为n,则(3)式可写成矩阵形式为:

利用有效独立法从可选测点总数n 中选择M 个节点作为测点,可得到结构表面M 个测点的法向速度:

根据上式,可以用M 个测点的法向振速通过逆向求解得到前N 阶模态坐标[q]N×1,进而对结构的整个表面的振速场进行重构。
分析(13)式构成的线性方程组,当M<N 时,(13)式为欠定方程组,[q]的解不唯一。故为了使[q]有唯一确定的解,要求测点数目至少与模态截断数目保持相等。
1.2 有效独立法基本理论
考虑白噪声影响,(12)式可表示为:

式中:υ 是方差为σ2的高斯白噪声。
有效独立法的基本理论是保证传感器能够得到尽可能多的线性无关的模态信息,实际上即是对模态坐标q 的最佳估计[11]。对应于q 存在偏差,假设(q为q 的无偏有效估计,估计偏差的协方差矩阵P可表示为:

式中:Q 为Fisher 信息矩阵[6]。
假设每个传感器的检测噪音误差都是相互独立且每个传感器的统计特性都是一致的,那么Fisher信息矩阵可以描述如下:

式中:A0=ΦTΦ。由上式可知,矩阵A0越大则协方差矩阵P 越小,即当A0最大时可获得q 的最佳估计。
矩阵A0的特征方程为:

式中:Ψ 是Q 的标准化特征向量,λ 是相应的特征值。
构造矩阵ED=ΦΨλ-1(Φ Ψ)T,可得:

矩阵ED对角线上的第i 个元素表示第i 个测点对模态矩阵线性无关性的贡献。有效独立法通过ED矩阵对角元素的大小对各个候选测点的优先顺序进行排序,用迭代算法每次排除ED对角元素最小的候选测点位置,再进行下一次的迭代,直至得到满意的布置点数[13]。
1.3 比例系数-有效独立法基本理论
尽管利用传统有效独立法可有效地估计结构的振动特性,但是它忽略了两个待选测点有相似的Fisher 信息矩阵的情况[12]。此时,虽然每个待选测点对模态矩阵线性独立性的贡献都很大,但是如果他们的信息矩阵是基本相同的,那么选择这两个测点得到的结构模态信息量和选择一个是基本相同的。
针对上述问题,本文定义模态振型比例系数为两个节点模态向量间的余弦值,用来评价测点之间的信息独立性,即:

式中:φi和φj分别为第i 和第j 个测点提供的模态振型,即模态矩阵的第i 行和第j 行,N 为模态截断数目。对于布置方案中任意两个测点,均满足:

当lij为0 时,说明两个测点提供的信息矩阵是相同的,则选择这两个测点得到的结构模态信息量和选择一个是相同的;当lij为1 时,两个测点提供的信息矩阵相互独立。
本文采用逐步累加的方式求解比例系数-有效独立法,以得到同时满足所选测点模态可测性和避免信息冗余的测点优化布置方案。具体步骤如下:
(1)首先按照(18)式计算出每个待选测点对模态矩阵线性无关性的贡献并排序,选择贡献量最大的待选测点作为第1 个测点位置。
(2)按照(19)式计算第1 个测点与剩余n-1 个待选测点之间的模态振型比例系数,选择比例系数最小值对应的待选测点作为第2 个测点位置。
(3)分别计算已选2 个测点与剩余n-2 个待选测点之间的模态振型比例系数,得到两个数组l1和l2。计算l1和l2中对应元素的均方差,选择均方差最小值对应的待选测点作为第3 个测点。如此,第3个测点与已选2 个测点的模态振型均能保持较大的线性无关性。
(4)重复步骤(3),直到确定全部M 个测点的位置。得到基于比例系数-有效独立法的圆柱壳测点优化布置方案。
1.4 测点布置方案评价准则
要判别一个测点布置方案的优劣,需要建立相应的评价标准,从而可以对测点布置方案进行评价[14]。下面分别从振动模态和响应的角度对评价准则进行介绍。
(1)基于振动模态的评价准则
由结构动力学原理可知,结构各固有振型在节点上的值形成一组正交向量,但由于量测的自由度远小于结构模型的自由度,且受外界环境的影响,测得的模态向量不能保证其正交性,甚至会由于向量间的空间夹角过小而丢失重要的模态。因此,在选择测点时有必要使测量的模态向量保持较大的空间夹角,从而尽可能地把原来模型的特性保留下来。
模态保证准则MAC(Modal Assurance Criterion)矩阵[15-16]是评价模态向量空间夹角的一个很好的工具,其公式表达如下:

式中:φi和φj分别为第i 阶和第j 阶模态向量。当MAC 矩阵中的某一元素等于1 时,表明这两阶模态向量空间夹角为零,其对应的模态振型不可分辨;当MAC 矩阵中的某一元素为0 时,表明这两阶模态向量相互正交,其对应振型可轻易识别。于是通过检查各阶振型在量测自由度上形成的MAC 矩阵的非对角元,即可判断出相应两个振型向量的夹角情况。
(2)基于振动响应的评价准则
测点优化布置的一个重要目的是为了能利用有限测点的响应来构造未测量点的响应。根据(3)式,可以用M 个测点的法向振速通过逆向求解得到前N 阶模态坐标[q]N×1,进而对结构整个表面的振速场进行重构。由于振动结构的辐射声场可由表面振速分布唯一地确定,通过声辐射边界元方法求得流体介质中的声传递矢量ATV(Acoustic Transfer Vector),即可得到声场中某一点辐射声压[10]。故本文以均方振速及场点辐射声压的结果对比来评价每种测点布置方案,均方振速及辐射声压的计算公式分别如下:

通过对比声场中某一点辐射声压的计算结果与预报结果,也可验证本文中的测点布置方法的可行性和有效性。
2 数值分析
本文以水下典型结构-单层加筋圆柱壳为研究对象。结构参数:总长L=1.02 m,半径R=0.425 m,肋骨间距l=0.075 m,环肋截面尺寸4 mm×33 mm,壳体厚t=0.004 m。材料参数:密度ρ=7 800 kg/m3,弹性模量E=210 GPa,泊松比μ=0.3,阻尼比ξ=0.005。
建模的坐标原点均位于模型左端面的中心,x、y、z 分别为水平、垂向和轴向。边界条件为结构两端约束x、y 两个方向上的平动,激励力为垂向单位力,激励力位置坐标为(0,-0.425,0.525),场点坐标(0,-100,0.525)。分析频率为0-1 000 Hz,间隔5 Hz。结构的周向和轴向网格数分别取为144 和56,节点总数为8 208。

图1 单层圆柱壳结构图Fig.1 Single-layer cylindrical shell
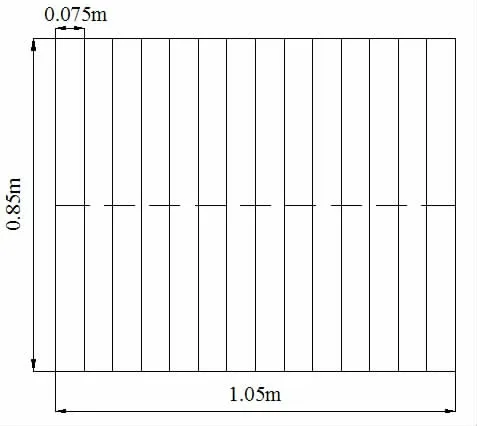
图2 单层圆柱壳尺寸图Fig.2 Dimension figure of cylindrical shell
2.1 模态分析
对上述圆柱壳结构进行模态分析及频率换算可知,将结构在空气中的振动模态从第64 阶截断即可满足水中振动响应分析的最高频率1 000 Hz,故模态截断数目需至少取为64。由于篇幅有限,并考虑到结构振动对称模态与反对称模态,表1 仅列出了结构第62~70 阶振动模态及对应的换算频率(m为轴向半波数,n 为周向波数)。

表1 固有频率换算表Tab.1 The conversion table of natural frequency
2.2 测点布置方案
根据上述理论分析,为使(13)式得到唯一确定的解,本文选取的测点数目与结构模态截断数目保持相等,即测点数目取为64。忽略结构边界处的节点,以剩下所有节点作为待选测点,则待选测点总数为7 920,故需从7 920 个待选测点中选取64 个作为测点。均匀测点的一种布置见图3所示(由于均匀测点布置方式的多样性,本文选择了多种布置方式中预报结果最好的一种作为对比),基于条件数的测点布置见图4所示,传统有效独立法得到的测点布置见图5所示,本文方法得到的测点布置见图6所示。
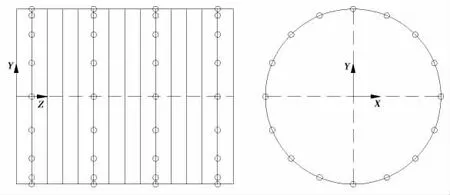
图3 均匀布置方法Fig.3 The uniform sensor displacement
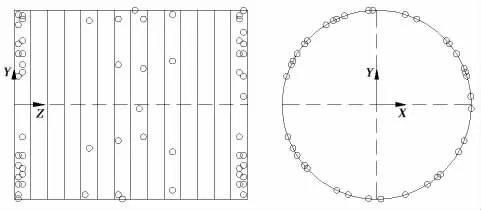
图4 基于条件数法Fig.4 Sensor displacement based on conditional number

图5 传统有效独立法Fig.5 Sensor displacement based on original EI
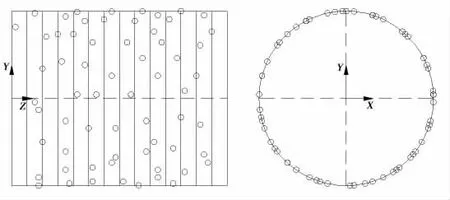
图6 本文方法Fig.6 Sensor displacement based on this paper
2.3 方案评价
下面分别从振动模态和响应的角度对上述测点布置方案进行评价。
(1)基于振动模态的评价准则
根据上述理论分析,MAC 矩阵的非对角元越小,所选测点的模态向量的空间夹角就越大,各阶模态向量就越容易被识别。上述四种测点布置方案对应的MAC 矩阵分别如图7-10所示,其中两水平轴代表模态阶次,垂直轴代表MAC 矩阵非对角元值,对角元素全部置为0。从图中可以看出,四种测点布置方案对应的MAC 矩阵非对角元的最大值分别为0.999 4、0.788 1、0.179 4 和0.165 6,其平均值分别为0.005 0、0.011 4、0.002 3 和0.001 8。并且,根据(21)式求得四种测点布置方案的模态振型比例系数的最大值分别为0.667 5、0.999 8、0.825 4 和0.4。可见,对于圆柱壳结构,采用本文中的比例系数-有效独立法得到的测点模态向量在保留结构的振动特性方面具有明显的优势。
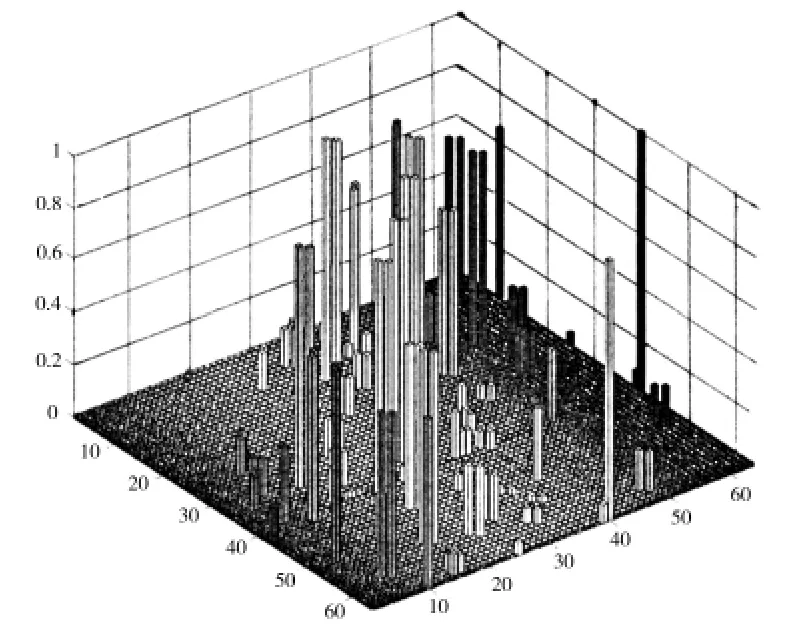
图7 均匀布置方法Fig.7 The uniform method

图8 基于条件数法Fig.8 Method based on conditional number

图9 传统有效独立法Fig.9 The original EI method
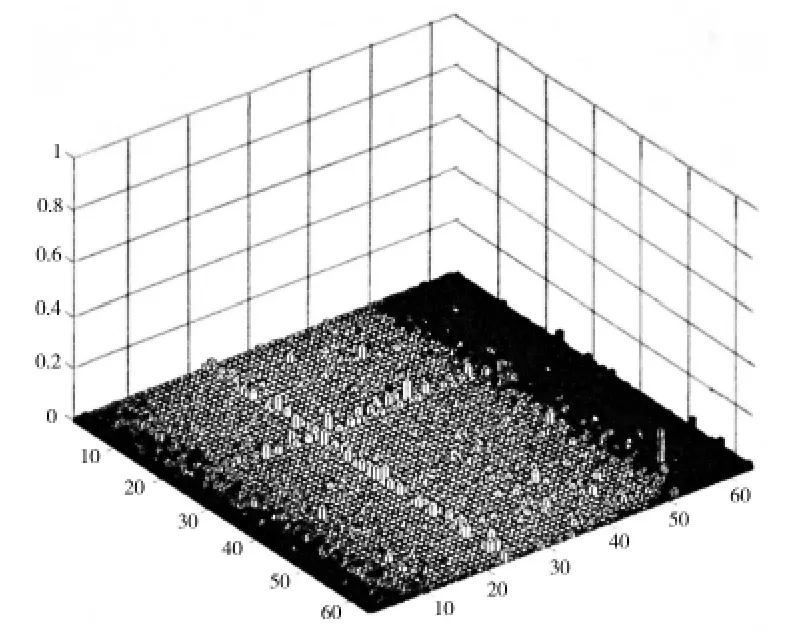
图10 本文方法Fig.10 Method of this paper
(2)基于振动响应的评价准则
由上述四种测点布置方案,得到结构均方振速及场点辐射声压的计算结果与预报结果的对比曲线如图11-12所示。从图中可以看出,采用均匀布置方法虽能得到较好的预报结果,但在测点选取上具有一定的盲目性,需要大量的计算和分析对比;基于条件数法在较低的频段内预报精度较高,但随着频率的增加,误差会相应增大;传统有效独立法在较高频率段内也会产生较大的误差,而本文方法得到的预报结果精度最高。进一步说明了本文方法是一种有效的测点优化布置算法。
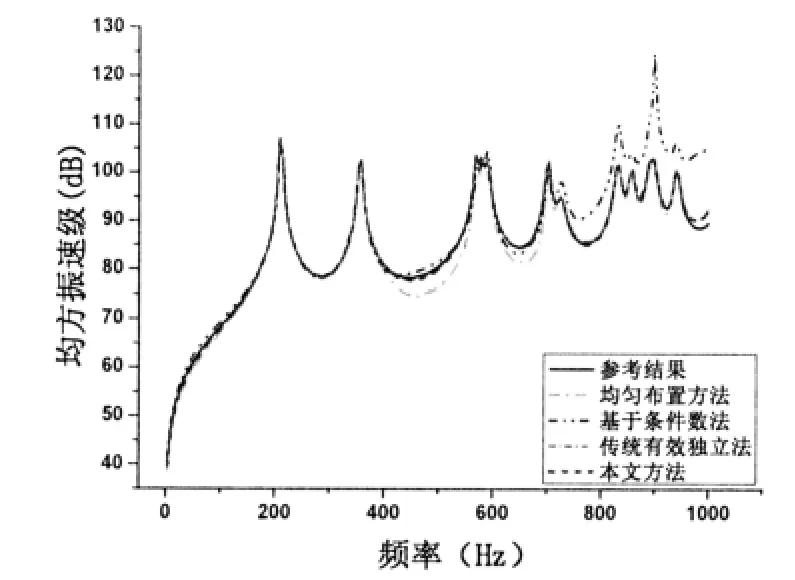
图11 法向均方振速级Fig.11 Normal mean-square-velocity
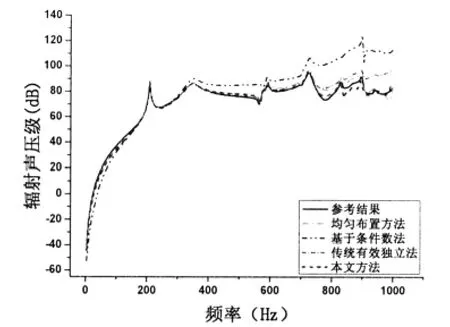
图12 场点辐射声压级Fig.12 Radiated sound pressure of field point
3 结论
本文针对圆柱壳结构的测点优化布置进行研究,并得到以下结论:
(1)在对传统有效独立法研究的基础上,提出了基于比例系数-有效独立法的测点优化布置算法,其以反映测点之间模态振型比例系数进一步优化了测点的选取。
(2)对比均匀布置方法、基于条件数法以及传统的有效独立法,本文方法得到的测点布置方案用基于模态和响应的准则进行评价的结果都很好。既能保证测量振型向量的正交性,又能对声振响应结果进行准确的预报。所以,本文提出的方法是一种有效的测点优化布置方法。

