基于裂纹尖端应力比值的FGM板应力强度因子简便预测方法

李 戎，杨 萌，梁 斌

（河南科技大学 土木工程学院，河南 洛阳471023）

0 引言

功能梯度材料（FGM）作为一种可设计性非均匀复合材料已经被广泛应用于船舶与海洋工程领域[1]。由于FGM 结构工作环境常为液体环境、大温度梯度等特殊极限环境，在服役期间经常受到冲击、腐蚀、突变载荷等作用而出现裂纹损伤。裂纹损伤不仅会影响结构性能，还有可能导致整个船舶与海洋工程结构失效[2-3]。而FGM 性质的连续性变化导致FGM 结构表现出与均匀材料结构不同的特性[4-11]，在壳体几何参数、载荷工况以及边界条件等相同的情况下，FGM 结构的力学行为分析要比相应均匀材料结构更为复杂。因此，需要针对含裂纹FGM 结构的非均匀性进行相应的力学行为分析。

近年来，虽然已经有研究论文涉及含裂纹FGM 结构这一领域[4-16]，但是由于FGM 的特殊性，这些研究所采用的计算方法往往复杂繁琐[4-8，14-16]，对使用者的推理能力以及计算能力要求较高，计算时间长，出错概率较高，难以满足实际工程应用需求。虽然已经有学者尝试改进计算方法，比如，选择节点布置更为自由的无单元法[7]，尝试降低裂纹尖端网格细分要求[12-13]。但是，现有研究仍然难以摆脱复杂的矩阵以及积分运算。课题组前期研究发现，不论是均匀材料还是异种接合材料，裂纹尖端应力强度因子均可以通过使用其与参考模型界面端应力的比值来进行求解[17-19]，而含裂纹均匀材料结构应力强度因子可由经验公式得到[7]。因此，如果能够找到均匀材料板和FGM 板之间裂纹尖端应力的稳定关系并加以利用，便可以在满足精度需求的基础上进行FGM 板应力强度因子简便预测。

为此，本文基于FGM 板与均匀材料板裂纹尖端应力之间的比例关系，提出了一种适用于FGM 板的应力强度因子简便预测方法。预测时，仅需使用由二维有限元模型得到的均匀材料板和FGM 板裂纹尖端应力值以及均匀材料板应力强度因子经验公式，便可在保证精确度的基础上进行预测。本文以含边缘裂纹有限宽FGM 板为例，给出了任意材料组分以及裂纹长度FGM 板的应力强度因子预测值，将本文预测结果与参考文献中的计算结果进行对比分析，验证了本方法的可行性和准确性。

1 力学模型

采用有限元软件MSC.Marc 建立如图1所示有限宽FGM 板二维模型，裂纹长度为a，板宽为W，材料沿x 方向连续性变化，板两端施加拉力，x 和y 分别为直角坐标系（x，y）的横向坐标和纵向坐标。

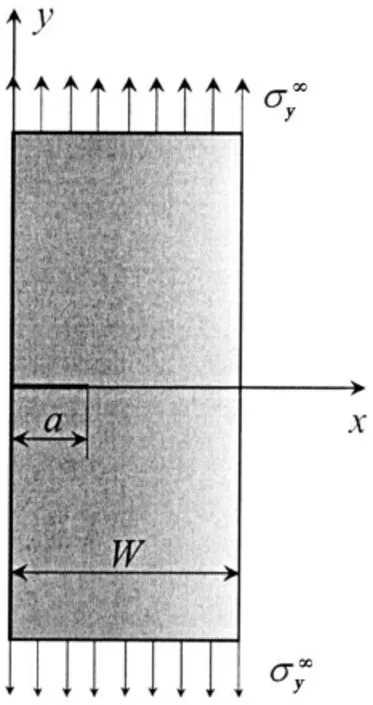
图1 FGM 板结构示意图Fig.1 Dimension for FGM plate

2 理论推导

根据线弹性断裂力学，当裂纹沿x 轴方向时（如图2所示），Ⅰ型裂纹尖端附近应力场可表示为[20]：

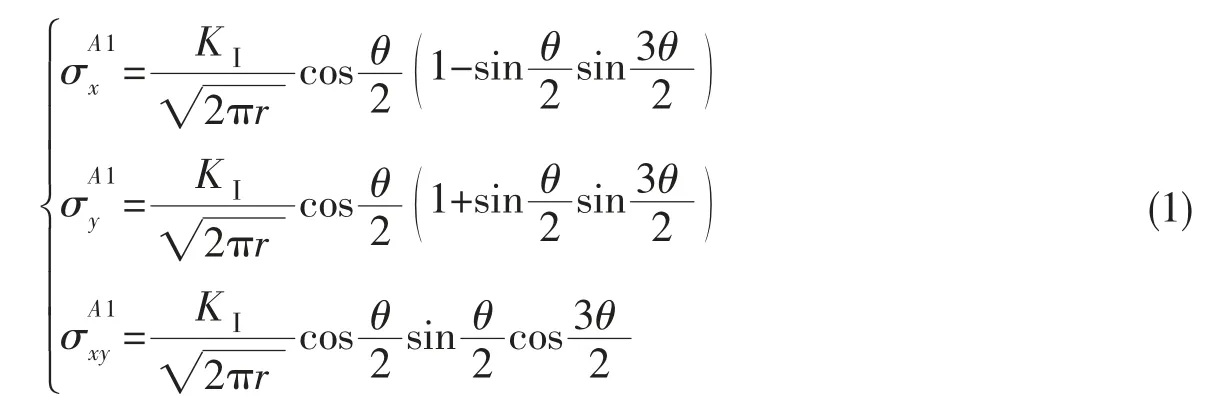
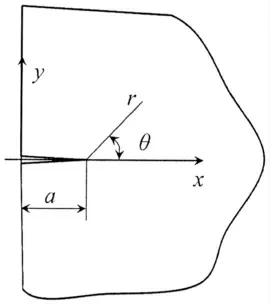
图2 裂纹尖端几何模型Fig.2 Schematic of edge crack in plate

式中：r 和θ 为裂纹尖端极坐标，a 为裂纹长度，KⅠ为Ⅰ型应力强度因子。

虽然FGM 和均匀材料裂纹尖端附近应力奇异性相同[21]，但是由于应力强度因子会受到材料梯度的影响[22]，公式（1）并不适用于FGM。因此，Erdogan[23]基于FGM 的材料特性，推导出了适用于FGM 的裂纹尖端附近应力场表达式：

式中：β 为与结构两侧材料弹性模量比值有关的参数。假设泊松比为一定值，E（）

x 为FGM 弹性模量，E（0）=E1，E（W）=E2，则β 和E（x）表达式为：

尽管FGM 和均匀材料裂纹尖端应力强度因子数值不同，但是两者应力奇异性相同，且应力奇异性不会受到材料梯度性影响[24]。当均匀材料板（*）与FGM 板的板宽、受力情况以及裂纹尖端附近网格划分完全相同时，这两者裂纹尖端附近应力比值与相应应力强度因子比值之间存在如下关系：

无量纲应力强度因子FⅠ和应力强度因子KⅠ满足关系式

取r=r*，当含边缘裂纹有限宽均匀材料板的已知，便可由公式（10）得到FGM 板的FⅠ预测值。

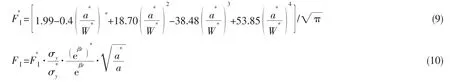
当r 足够小时，eβr（）*/eβr≈1。此时，裂纹尖端附近应力比值等于其应力强度因子比值，则公式（10）可简化为公式（12）。当E2/E1=1 时，FGM 板退化为均匀材料板。

3 算例与讨论

由于裂纹尖端应力奇异性的存在，使用有限元软件得到的应力数值σy会随裂纹尖端附近网格尺寸以及r 的改变而发生变化，不能直接使用σy来计算应力强度因子。但是，当两个模型宽度、受力、裂纹尖端附近网格划分完全相同，并且裂纹尖端附近最小网格尺寸emin足够小时，两个模型裂纹尖端应力比值稳定不变，应力奇异性可通过比值形式消除[17-19]，可由公式（12）进行FⅠ预测。

表1给出了不同emin时裂纹尖端应力分布情况以及相关预测数据。采用有限元软件MSC.Marc 建立如图3所示的二维有限元模型，板宽W=1 m，两端施加拉力，使用平面应变四节点四边形单元，裂纹尖端附近网格加密，emin=1/39m 时单元总数为29 911，其中裂纹尖端附近单元数约为20 000。当E2/E1=1 时，FGM 板退化为均匀材料板。

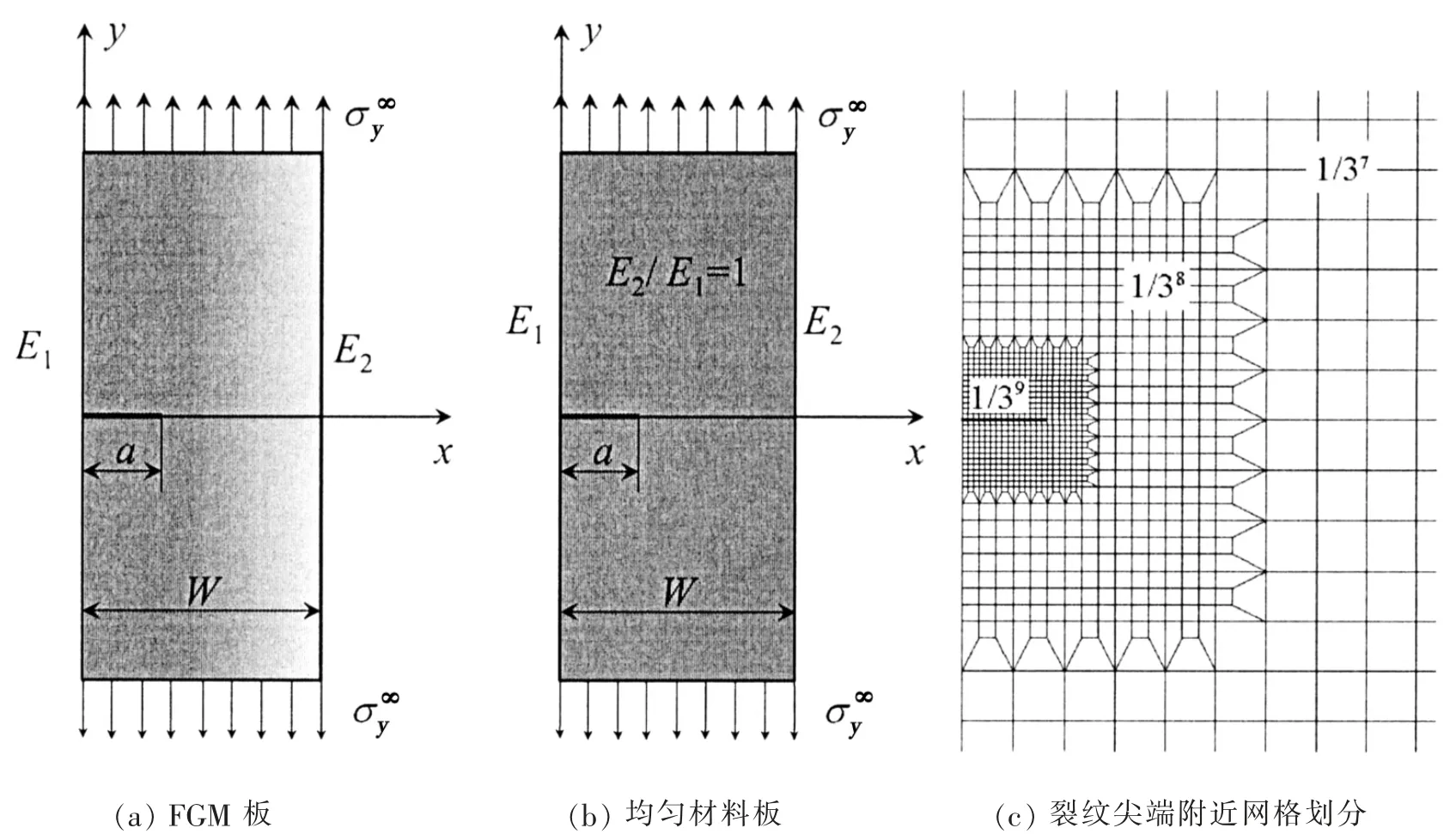
图3 模型网格划分示意图Fig.3 Mesh pattern for model

表1 不同网格尺寸时裂纹尖端应力分布及无量纲应力强度因子FI 预测Tab.1 Stress distributions and predicted values of dimensionless stress intensity factor FI for crack tip obtained by different mesh sizes

图4给出了分别采用公式（10）以及公式（12）得到的预测值之间的误差（%），r=0，emin=1/39m。从中可以看出，当emin足够小时，预测结果稳定，预测结果基本不受裂纹尺寸以及材料组分影响，误差可控制在0.2%以内。此时，eβr的影响可以忽略不计，使用公式（12）即可满足预测需求。

表2 中给出了采用本文方法得到的任意FGM板FI预测结果以及文献[6]的计算结果。结果表明，预测结果与文献计算结果非常接近，预测精度良好。预测结果中，近80%预测误差可控制在0.5%以内，最小预测误差仅为0.006%。当a /W＞0.6，E2/E1＜2 时，预测误差有增大趋势，结果中共有2 组数据误差超过5%，但预测误差仍控制在12%以内。误差产生原因可能与本文预测方法是基于裂纹尖端应力比值、而文献采用围线积分法有关。

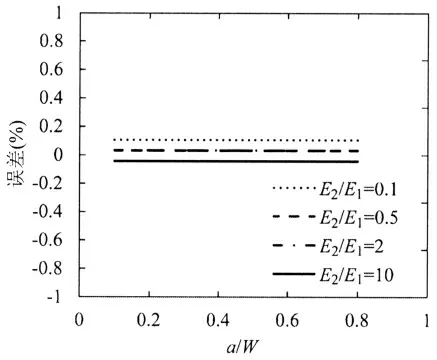
图4 预测误差对比分析Fig.4 Comparison of predictive errors

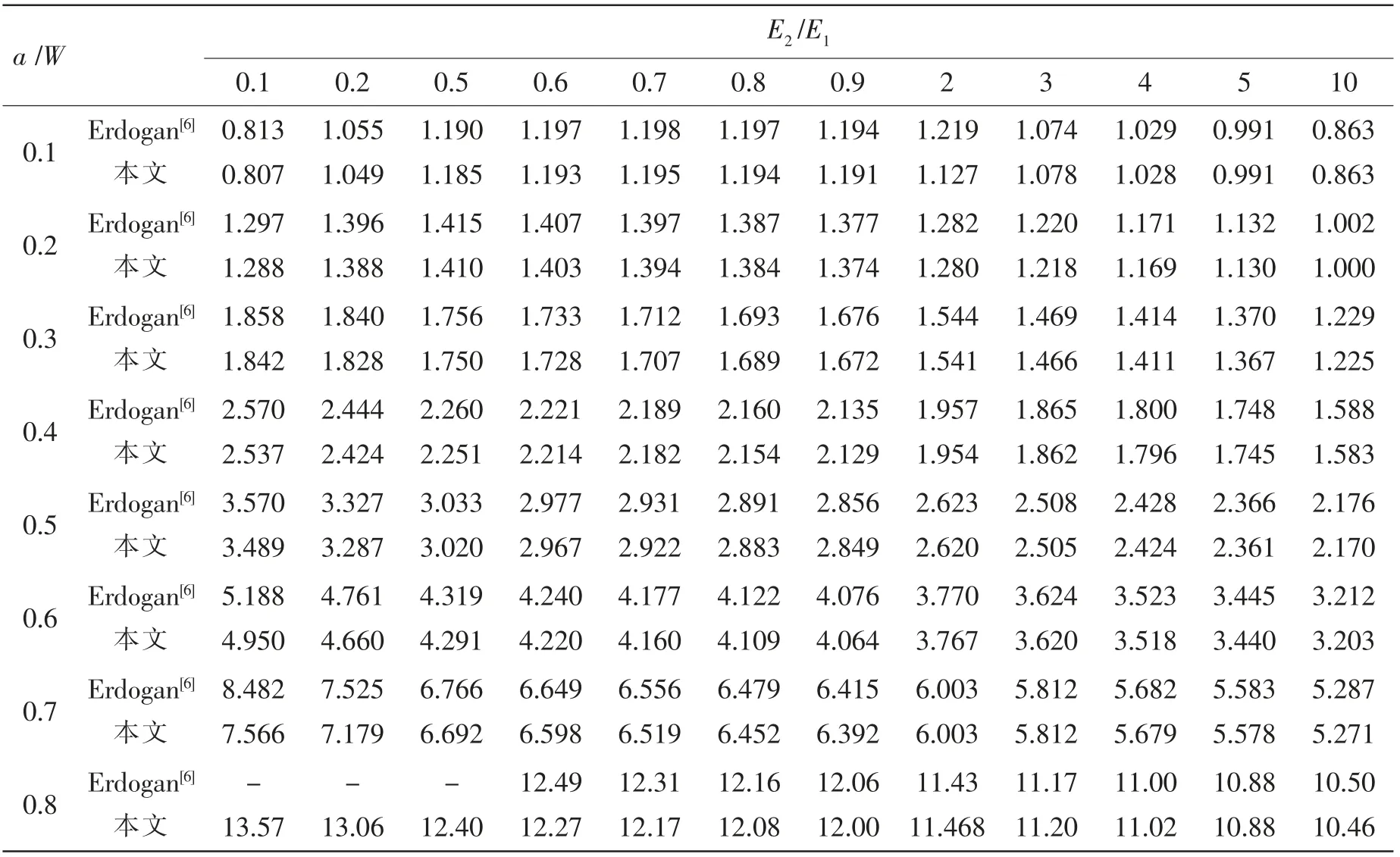
表2 无量纲应力强度因子FI 预测值Tab.2 Predicted values of dimensionless stress intensity factor FI

图5给出了本文预测方法与其他传统计算方法的结果对比图。可以看出，本文预测结果与现有计算方法的计算结果[5]几乎完全一致；当a /W＞0.4 本文预测结果优于采用Node release technique (G)[5]得到的计算结果，完全满足精度要求。与参考文献[5-6]中使用的计算方法相比，本文方法预测时所用可任意选取，且预测过程免去了复杂的矩阵以及积分运算，预测精度高，计算量小，适合工程应用。

图5 预测方法对比分析Fig.5 Comparison of prediction methods

表3 无量纲应力强度因子FI 预测值(：FGM 板）Tab.3 Predicted values of dimensionless stress intensity factor FI（：FGM plate)

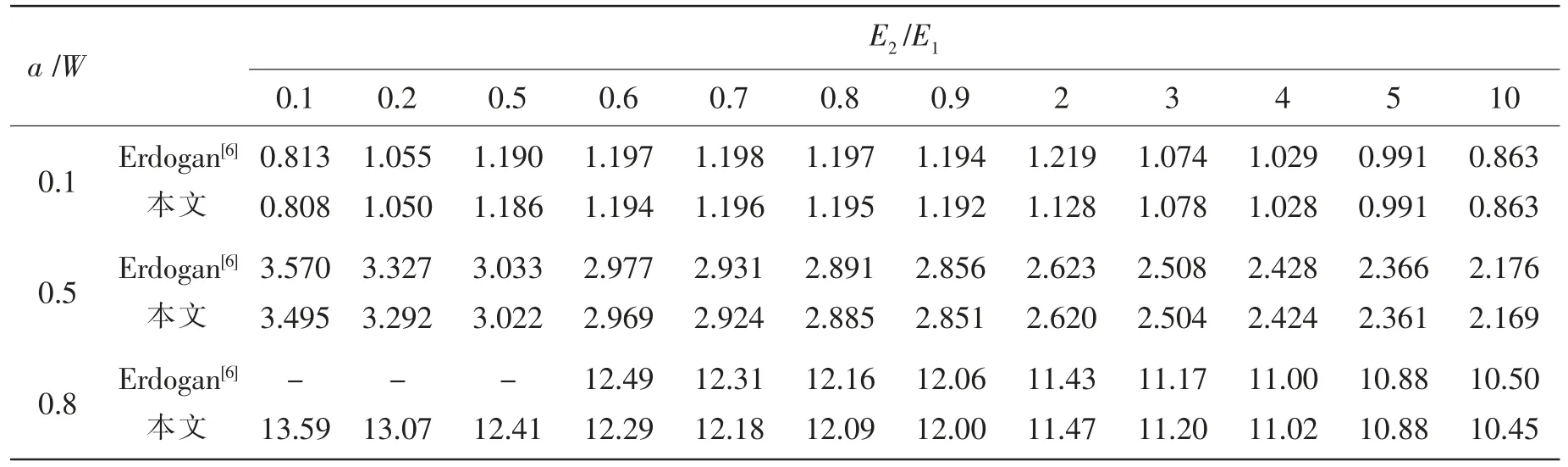
表3 无量纲应力强度因子FI 预测值(：FGM 板）Tab.3 Predicted values of dimensionless stress intensity factor FI（：FGM plate)

a /W E2/E1 0.1 0.2 0.5 0.6 0.7 0.8 0.9 2 3 4 5 10 0.1 Erdogan[6]本文0.863 0.863 0.5 Erdogan[6]本文0.813 0.808 1.055 1.050 1.190 1.186 1.197 1.194 1.198 1.196 1.197 1.195 1.194 1.192 1.219 1.128 1.074 1.078 1.029 1.028 0.991 0.991 2.176 2.169 0.8 Erdogan[6]本文3.570 3.495 3.327 3.292 3.033 3.022 2.977 2.969 2.931 2.924 2.891 2.885 2.856 2.851 2.623 2.620 2.508 2.504 2.428 2.424 2.366 2.361---13.59 13.07 12.41 12.49 12.29 12.31 12.18 12.16 12.09 12.06 12.00 11.43 11.47 11.17 11.20 11.00 11.02 10.88 10.88 10.50 10.45

本文预测方法是基于裂纹尖端应力比值，预测精度高、方法简便实用，但是对裂纹尖端附近网格细化程度有一定要求。因此，在使用本文方法进行应力强度因子预测时，需尽量选择裂纹尖端附近应力比值稳定不变时所对应的网格尺寸emin。本文预测方法不仅适用于FGM 板，还可用于其他FGM 结构的应力强度因子预测，但是现有预测研究结果还很有限，本项目后续工作将进行深入研究。

4 结论

本文基于FGM 板与均匀材料板裂纹尖端附近应力之间的比例关系，提出了一种适用于FGM 板的应力强度因子简便预测方法。该方法仅通过使用均匀材料板和FGM 板裂纹尖端应力比值、均匀材料板应力强度因子经验值即可在保证精确度的基础上快速得到任意FGM 板应力强度因子值，计算过程避免了复杂的矩阵以及积分运算，计算量小，研究效率高。预测结果显示，本文预测方法适用于任意裂纹尺寸以及材料组分的FGM 应力强度因子预测，且该预测方法不受参考模型应力强度因子限制，可任意选取，预测方法精度高、预测结果稳定，便于工程应用。