大型集装箱船快速波激响应分析

林 源，马 宁，顾解忡

（1.上海交通大学 海洋工程国家重点实验室，上海200240；2.高新船舶与深海开发装备协同创新中心，上海200240）

0 引言

随着全球经济逐渐一体化，为实现航运的规模效应，集装箱船的大型化日益加剧。集装箱船尺度的增加，相应地也会带来甲板大开口的现象，随之带来船体梁固有频率下降，而航速的提升会增高波浪遭遇频率，从而会引起船体的共振或强迫振动，将影响船舶的使用寿命。所以在大型集装箱船的设计制造过程中，水弹性响应分析（如：波激振动）应当被重视。

目前有关船舶水弹性理论已有较为全面的发展。最为经典的水弹性理论就是Bishop 和Price[1]提出的二维理论，然而其忽略流体运动沿船长方向的相互干扰，并未能计及船体首部和尾部的三维效应[2]。接下来Wu[3]，Price 等[4]提出三维水弹性理论，是将三维耐波性与三维结构动力学相结合，但是三维理论需要大量的船体网格。

针对在工程上的快速水弹性预报，三维水弹性理论需要建立大量船体网格，工作量较大。因而简化网格对于数值计算是必然的，Golberg[5]和Fairweather 等[6]证明了MFS（The method of fundamental solutions）作为一种无网格方法在水动力计算上的优越性，但现阶段MFS 方法尚未用于水弹性响应的求解。而且有关的三维有限元与二维耐波性混合模型研究较少，Wang 等[7]将其应用到浮体结构中，但运用到船舶响应求解极少。本文提出一种混合水弹性模型，利用三维有限元方法预报船舶的固有模态，再基于MFS 方法的STF 切片理论[8-9]，进行固有模态下的无网格船体广义流体力计算，最后根据模态叠加法求解船舶在波浪作用下的波激振动分析。为验证本方法的计算精度，采用Bernoulli 梁垂向振动模态振型的解析解和水动力软件HydroSTAR 的数值计算结果进行验证。

1 船体固有模态预报及波激振动

根据船舶水弹性统一理论，得到船舶在波浪作用下振动的响应方程

其中：a，b 和c 分别表示船体广义的结构质量、阻尼、刚度矩阵，是N×N 对角矩阵，每个矩阵分别由矩阵系数arr，brr和crr组成，通过结构模态分析获得。流体广义质量、阻尼、刚度矩阵分别由A、B 和C 表示，由矩阵系数Ars，Brs和Crs构成，并通过基于MFS 方法的STF 切片方法进行求解。pa和F 分别表示为主坐标和广义干扰力矩阵。ωe为遭遇频率。

1.1 模态分析

1.1.1 干模态分析

干模态法是先把结构系统与流体分开，求出真空中结构的固有频率和固有模态，即干模态[10]。根据实际需要进行模态分离，使自由度数目减少。基于干模态坐标变换下，再进行考虑流体的作用。

根据动力平衡方程有

其中：M、C、K 分别为系统的质量矩阵、阻尼矩阵和刚度矩阵，F（t）为载荷向量，、、r 分别为节点的加速度、速度和位移向量。

真空中结构无阻尼自由振动方程如方程（3）所示，可通过求解得到相应的固有频率和固有模态。

假设系统做简谐运动，即为

其中：ω 为频率，A 为振幅向量，将方程（4）代入方程（3）可得：

若使得方程（5）有非零解，A 不全为零，则有特征方程如下，解此方程得到的响应的特征值和特征向量，即为相应船体干模态的固有频率ω 和固有振型。

MSC.Patran&Nastran 软件[11]利用其经验公式，已给出计算结果精度极高的方法。通过模态分析（Modal analysis），得到固有模态频率ω 和固有模态振型，并导出振型归一化的模态质量阵a 和模态刚度阵c。对于结构的广义阻尼阵b 的相关计算可以按下列方程[10]进行计算，其中

其中：v 为阻尼系数，ωr为r 阶模态下的固有频率，arr为r 阶模态广义质量。小阻尼情况下，对数衰减率为δ≈2πv。一般情况下，其经验公式如（8）式所示，从而可得到相应的阻尼系数。

1.1.2 湿模态分析

船体的附连水振动质量在MSC.Patran&Nastran 内是通过定义有限元模型湿表面单元号码和船舶的吃水来自动实现其计算，其理论是用Helmholtz 方法即源汇法（也叫边界元法）解流体运动的拉普拉斯方程。湿模态是计及周围水动力影响的结构系统的无阻尼自由振动模态，可通过有限元软件中设置相关的参数[11]求解湿模态。

1.2 广义流体作用力

对于有航速的船体广义流体质量、阻尼和刚度矩阵元素[1]如下所示：

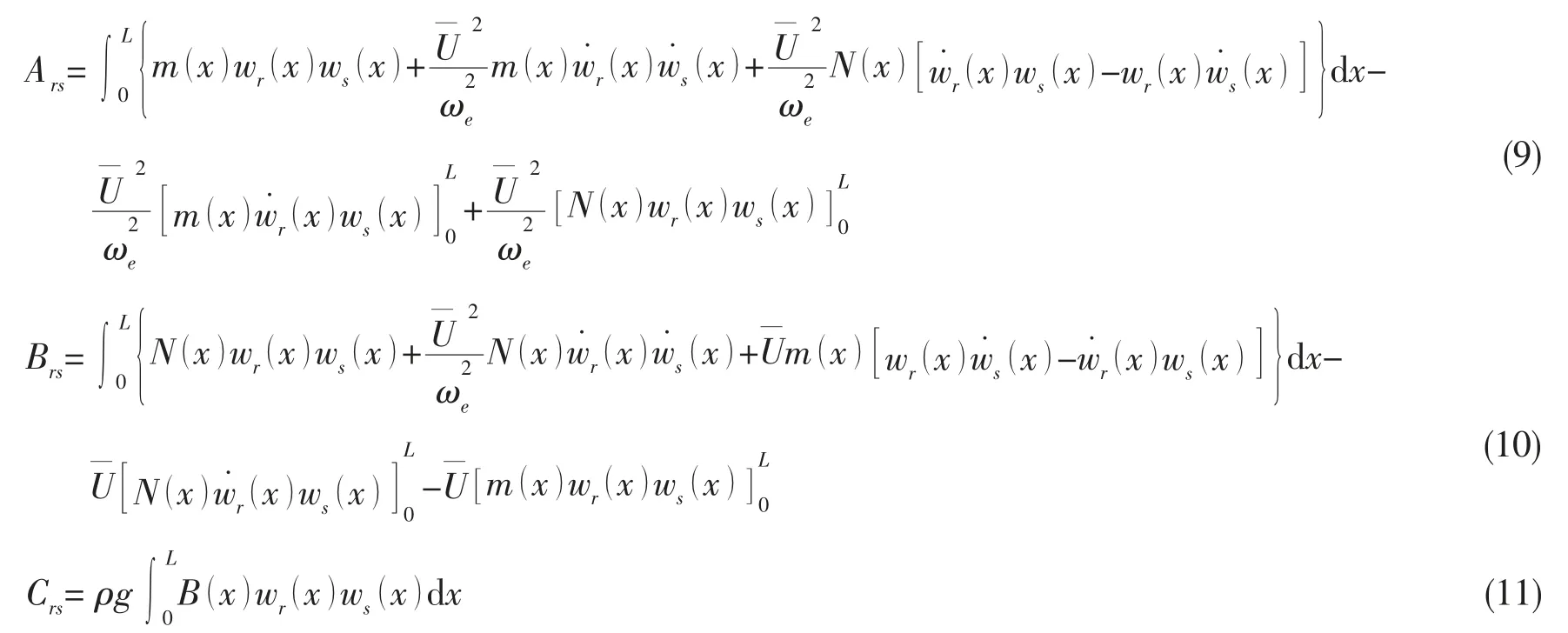
其中：m（x），N（x），B（x）分别为单位船体上的附加质量、流体阻尼系数和微片宽度。对于广义流体质量、阻尼和刚度矩阵元素的积分，将Feng 等人[9]利用MFS 无网格方法求解船体水动力系数的方法，应用到基于固有模态下的广义流体作用力系数的求解。

1.3 波激响应

经过上述计算，可以得到船体的广义质量阵a、阻尼阵b 和刚度阵c，及流体广义质量阵A、阻尼阵B、刚度矩阵C 和波浪激励力阵F，便可列出船体的波激振动模态分析方程[10]，即得到相应的主坐标Pa，从而可以求得船体在波浪作用下垂直弯曲振动的动位移w（x，t）、动弯矩M（x，t）和动切力V（x，t）等动力响应。

2 模型精度验证

为验证计算模型的精度，本文通过三维有限元固有模态计算结果与Bernoulli 梁的解析解[10]（如方程（15）所示）对比，从而对固有模态的求解精度进行了验证。

图1 Bernoulli 梁1 阶模态的三维有限元计算结果与梁解析解对比Fig.1 The comparisons between the first order model shapes of Bernoulli beam by 3D FEM and the analytical solution

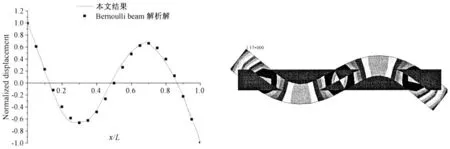
图2 Bernoulli 梁2 阶模态的三维有限元计算结果与梁解析解对比Fig.2 The comparisons between the second order model shapes of Bernoulli beam by 3D FEM and the analytical solution

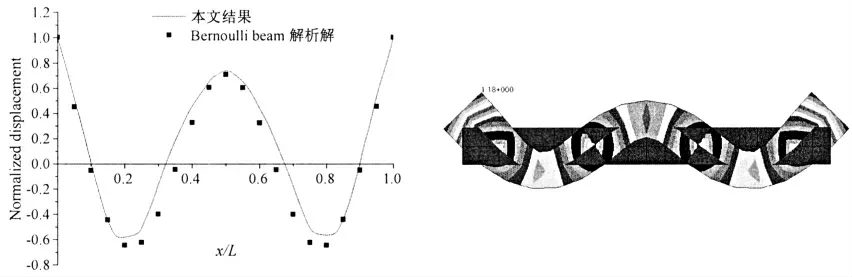
图3 Bernoulli 梁3 阶模态的三维有限元计算结果与梁解析解对比Fig.3 The comparisons between the third order model shapes of Bernoulli beam by 3D FEM and the analytical solution

其中：kr为特征值，其取值满足如下特征方程：cos krL·cosh krL=1。关于三维有限元结果和Bernoulli 梁的解析解，这里均采用了将船尾处的位移归一化为单位1，方便对比分析。根据剖面上的点位移转角和剖面存在一定的几何关系，将三维Bernoulli 梁模型模态分析后剖面的节点的位移回归得到归一化的振型图。图1 至图3 分别给出了1 至3 阶固有模态计算结果和解析解的对比。其中1 阶和2 阶模态计算结果能够与解析解达到90%以上的重合程度。从而证明应用三维有限元方法进行波激振动的固有模态分析，较迁移矩阵随迭代而逐步叠加误差，能为进一步基于模态振型下的流体水动力系数求解提供更高的精度。

通过ANSYS 软件对于三维有限元模态分析结果进行交叉的计算验证，通过表1 可看出，MSC.Patran&Nastran计算结果有保证。

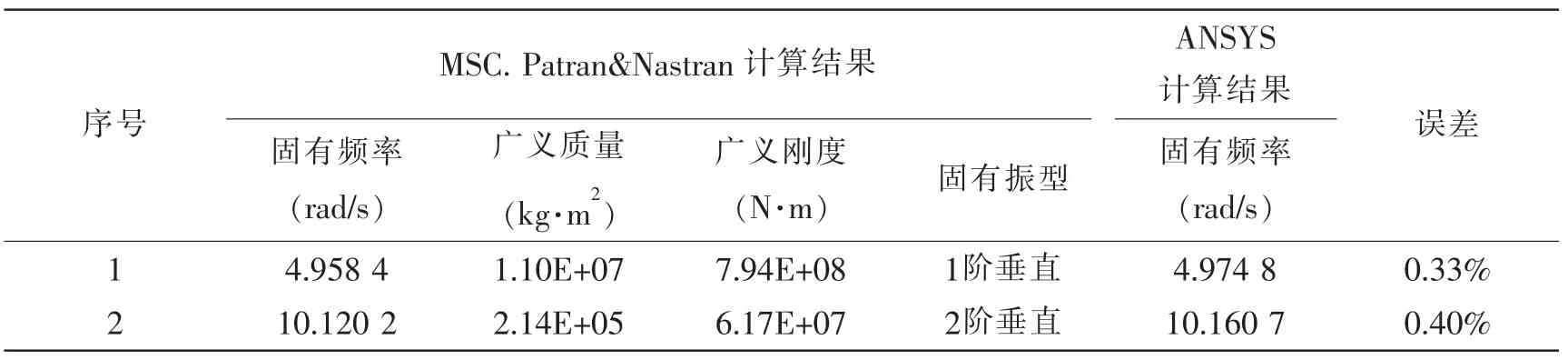
表1 MSC.Patran&Nastran 与ANSYS 计算固有模态对比分析Tab.1 Comparisons on modal analysis results between MSC.Patran &Nastran and ANSYS

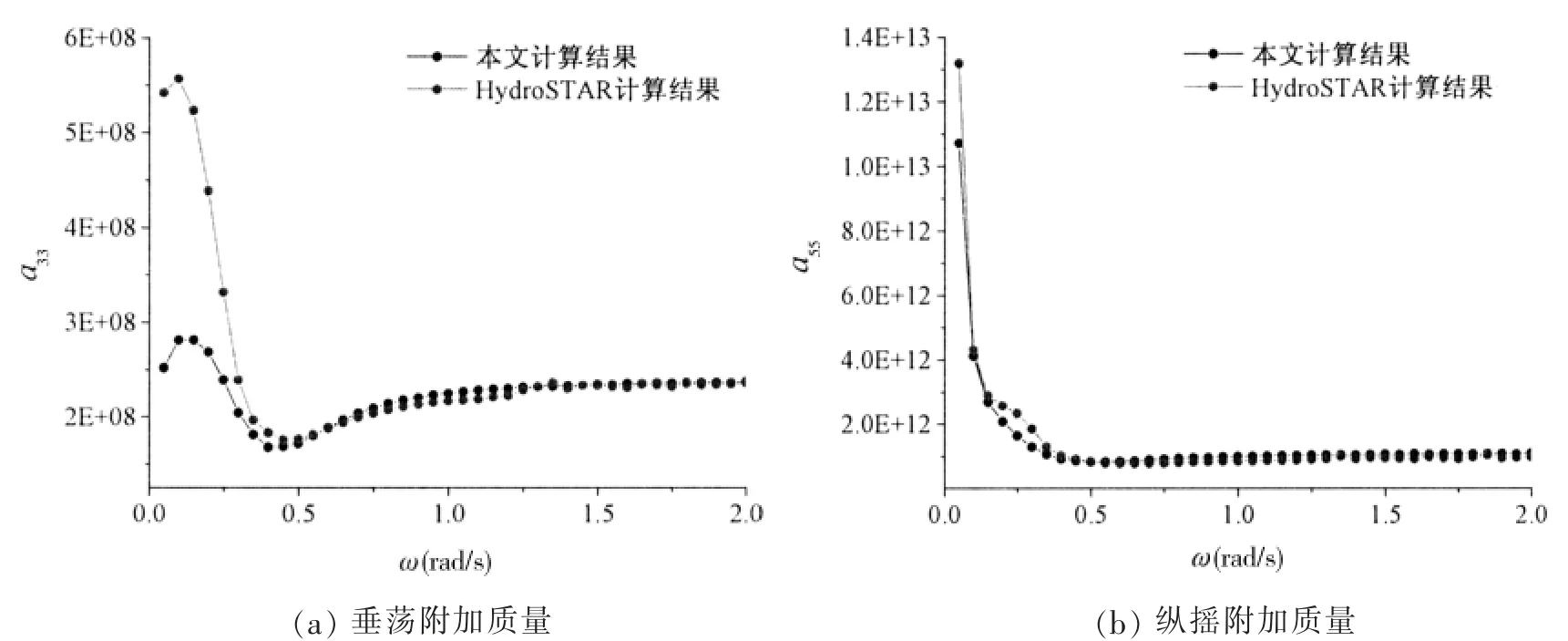
图4 大型集装箱船垂荡和纵摇附加质量曲线Fig.4 Heave and pitch added mass of very large container ship

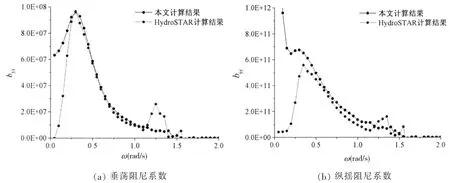
图5 大型集装箱船垂荡和纵摇阻尼系数曲线Fig.5 Heave and pitch damping of very large container ship

本文为验证模型耐波性部分计算的正确性，计算了迎浪状态下、100%服务航速时大型集装箱船的垂荡和纵摇的附加质量、附加阻尼和激励力，与商业软件HydroSTAR 计算的结果对比分析，如图4 至图6所示。在中高频波浪下，本文的计算结果精度可以满足，对于由于切片法本身的弊端，低频情况下的精度上仍需改善。但是总体上的误差在15%以内，并且由于低频部分对于波激振动趋势的展示影响较小，故而可以满足工程需求。

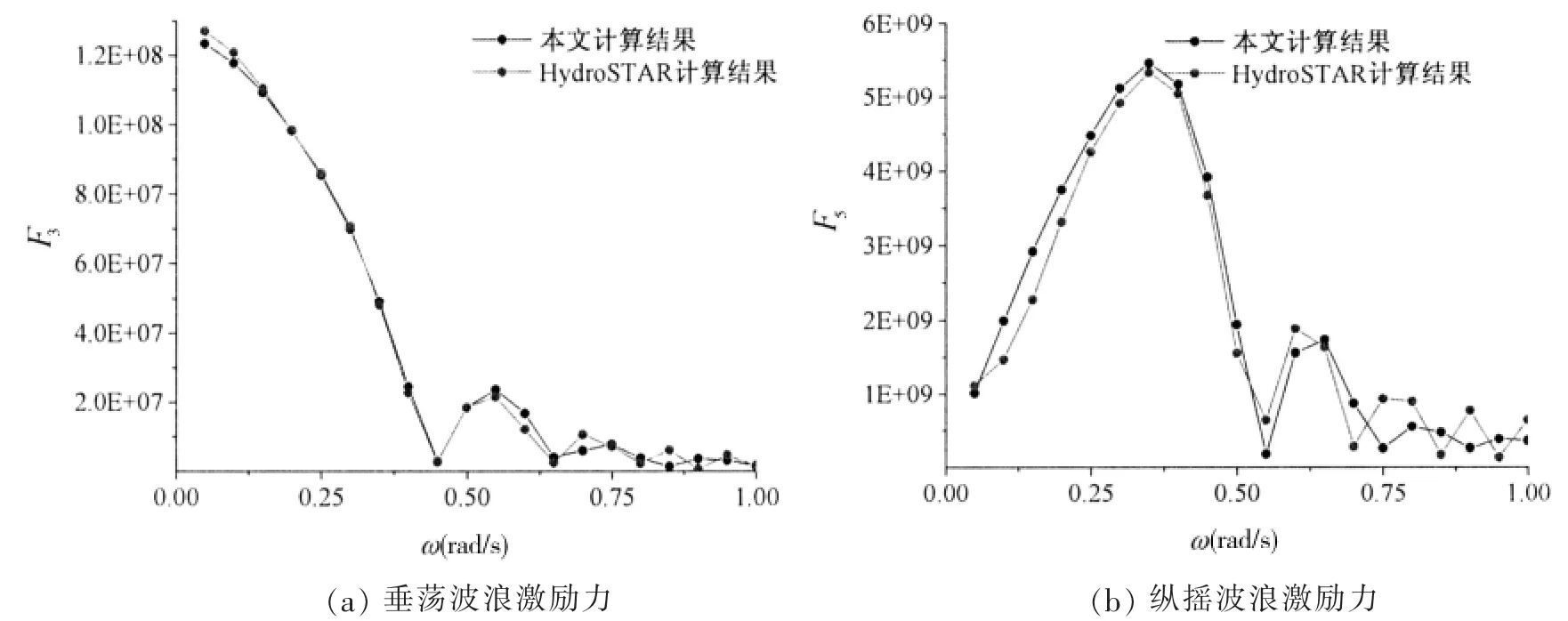
图6 大型集装箱船垂荡和纵摇波浪激励力曲线Fig.6 Heave and pitch excitation of very large container ship

3 大型集装箱船波激振动分析

对大型集装箱船的有限元分析，是通过MSC.Patran &Nastran 软件，得到了各阶固有干模态的固有振型及相应的广义质量、广义刚度，并通过经验公式得到相应的广义阻尼，汇总成表，如表2所示。

表2 大型集装箱船的干湿模态预报结果及结构广义质量、刚度、阻尼值Tab.2 Dry and wet mode prediction and the generalized mass,damping and stiffness

根据剖面上的点位移转角和剖面存在一定的几何关系，将三维集装箱船模型模态分析后剖面的节点的位移回归得到归一化的振型图。其中大型集装箱船的第1 阶至第3 阶对称振动的固有振型图，如图7 至图9所示，考虑到大型集装箱船的宽大型、大甲板开口复杂性，采用三维有限元方法对船舶进行模态分析，计算结果与船体梁的迁移矩阵模态分析相比，精准度较高。

图7 某大型集装箱船1 阶垂向模态振型图预报Fig.7 The predicted results on first order mode shape of very large container ship

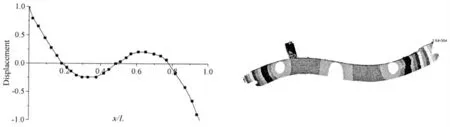
图8 某大型集装箱船2 阶垂向模态振型图预报Fig.8 The predicted results on second order mode shape of very large container ship

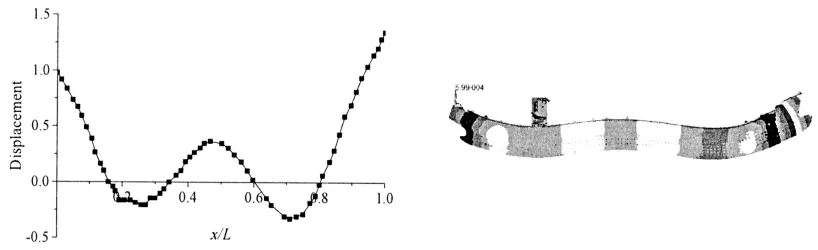
图9 某大型集装箱船3 阶垂向模态振型图预报Fig.9 The predicted results on third order mode shape of very large container ship

通过上述模态分析，将回归后的归一化振型运用到广义流体作用力的计算，从而进一步可以求解相应的波激对称振动方程。为考虑航速对于主坐标的影响，采用迎浪下100%服务航速和50%服务航速的数值计算，可以通过图10 看到对称响应主坐标幅值随船长与波长之比L/λ 变化趋势。对于第1阶和第2 阶垂直弯曲模态，其主坐标变化趋势相同，且第1 阶主坐标最大幅值大于第2 阶主坐标最大幅值，具有船舶波激响应的一般趋势。当航速增大时，主坐标的数值相应也有一定程度的增大，并且第一个峰值皆出现在L/λ=1 处，证明了计算结果的准确性。随着遭遇频率的增加，在L/λ≈8.75 和18.68 时产生第二个和第三个峰值。根据波长与波频关系式有L/λ=Lω2/2πg，遭遇频率ωe=ω-ω2Ucos β/g，可以求出对应L/λ≈8.75、18.68 时，遭遇频率为2.353 rad/s 和4.147 rad/s，说明本方法的可行性。而且较三维水弹性方法，采用无网格MFS 的STF 法求解流体水动力系数可简化网格，降低计算难度和节省时间。

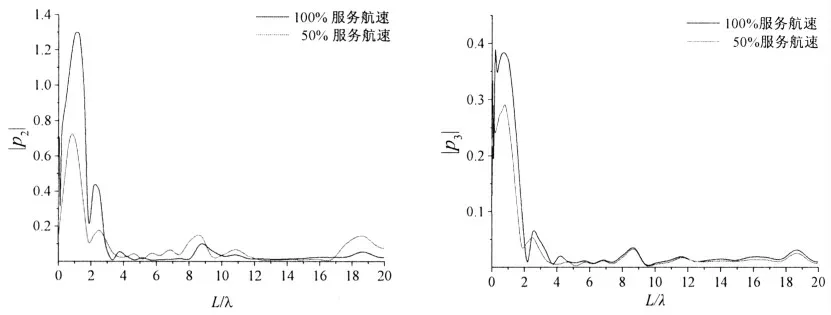
图10 不同航速迎浪航行时的主坐标和变化曲线（左图为，右图为）Fig.10 The third and fourth principal mode curves of various speeds in the heading sea

4 结论

本文以集装箱船为目标船型，提出了三维有限元结构分析与二维耐波性分析相结合的水弹性预报方法，并基于该方法对某大型集装箱船的波激响应进行了分析：

（1）本文方法较目前的三维水弹性分析大幅简化了网格划分、提高了计算效率；且与二维水弹性方法相比，在结构分析时能够提高精度，具有较好的工程实用价值；

（2）本文通过MSC.Patran &Nastran 软件模态分析得到的固有振型方法，经过梁模型验证，平均精度在90%以上；计算的固有频率，与ANSYS 软件计算结果相比，精度有保证；

（3）本文基于STF 切片理论计算的广义流体相关系数，忽略船体变形的刚体运动，与三维HydroSTAR软件对比，精度在85%以上，具有工程实用价值，但在未来阶段仍需改进低频部分的精度问题；

（4）基于本文模型得到的波激对称响应，符合船舶水弹性相关特性，得到共振的遭遇频率分别为2.353 rad/s 和4.147 rad/s。