轮轨滚动接触和制动热负荷耦合作用对重载车轮踏面裂纹萌生寿命的影响

李 兰，蔡园武，郭 刚

(1.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081；2.中国铁道科学研究院集团有限公司 高速轮轨关系试验室，北京 100081)

随着铁路货车速度的提高和轴重的不断增加，列车动能也急剧增加，必然要求车辆制动力相应地提高；另一方面，随着轴重的增加轮轨接触应力也随之增大。在制动热负荷和轮轨滚动接触载荷的复杂耦合作用下，车轮踏面可能出现热斑、裂纹和剥离等损伤，从而产生行车安全隐患。目前对车轮踏面热负荷伤损产生和演化的数值模拟较少，对裂纹的形成原因、形成机理尚有待深入研究。因此，急需对制动工况和轮轨滚动接触耦合作用下大轴重车轮热损伤的安全性进行研究。

虽然国内外学者对货车车轮热负荷开展了大量研究[1-4]，但是在这些研究中制动产生的热流及温度场多考虑为沿圆周均匀分布，无法反映闸瓦与车轮踏面实际摩擦接触过程中产生的瞬态非均匀热流分布,且研究接触压力和制动热负荷共同作用下的疲劳问题时采用的是间接耦合法。

本文采用考虑车轮踏面制动瞬态非均匀热流分布的热—机耦合三维有限元模型并结合纵向动力学模型和疲劳损伤仿真分析模型，计算了典型长大下坡道循环制动条件下的大轴重车轮踏面疲劳裂纹萌生寿命，研究闸瓦制动热负荷和轮轨滚动接触耦合作用对裂纹萌生寿命的影响。

1 长大下坡道循环制动车轮踏面裂纹萌生寿命计算方法

在制动过程中，特别是在长大下坡道循环制动过程中，一方面，由于车轮制动，车轮踏面将一直承受热载荷作用，车轮踏面温度及温度梯度变化均十分剧烈；另一方面，车轮每旋转1周，均受到1次较大的轮轨接触应力循环作用。在这种复杂的耦合作用下，极易萌生车轮踏面裂纹。采用列车纵向动力学分析和有限元分析计算得到长大下坡道循环制动条件下车轮的温度场和应力应变结果，导入到FE-SAFE疲劳寿命分析软件中分析得到车轮裂纹萌生寿命，流程如图1所示。

由图1可见：首先，采用列车纵向动力学分析得到长大下坡道循环制动过程中车辆速度和闸瓦压力时程曲线；根据这2个时程曲线，采用瞬态三维有限元分析方法获得车轮踏面热应力应变时程曲线。其次，采用轮轨接触力学分析模型计算得到轮轨接触应力应变时程曲线；最后，将轮轨接触应力与制动热应力进行叠加，获得材料应变ε—寿命N曲线。

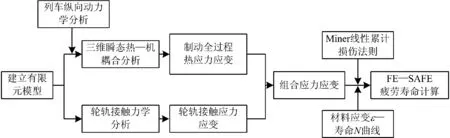
图1 踏面制动和轮轨滚动接触耦合作用下踏面裂纹萌生寿命分析方法流程

值得注意的是，由于主应力方向不断发生变化，在开展长大下坡道循环制动车轮踏面裂纹萌生寿命分析时，单轴疲劳分析方法并不适用，因此采用临界平面准则进行疲劳分析。

2 三维瞬态热—机耦合有限元模型的建立及验证

2.1 模型建立

前期研究结果表明，无论是采用车轮—闸瓦模型还是采用车轮—闸瓦—轨道模型对制动全过程温度计算结果的影响极其微小，同时车轮—钢轨模型和车轮—闸瓦—钢轨模型对轮轨接触应力的计算也几乎没有影响[5]。因此，本文计算模型采用单个车轮与闸瓦接触的有限元模型。

采用有限元软件Abaqus建立闸瓦—车轮三维有限元模型。车轮选用重载铁路上常用的Φ915 HFS车轮，其材料采用CL70钢，踏面为LM型面。闸瓦选用HGM-A型高摩合成闸瓦。车轴中心处除绕轴旋转自由度外，其他自由度均施加约束。对闸瓦钢背孔处的轴向和踏面切向方向自由度施加约束。为模拟实际轴重的惯性作用，轴上增加惯性轮，并把一半轴重的动能等效到惯性轮上。车轮和闸瓦均采用ABAQUS软件中的8节点热耦合实体单元C3D8RT进行离散，车轮踏面与闸瓦接触处的单元尺寸为3 mm。为提高计算效率，车轴和惯性轮采用刚性连接。闸瓦与车轮踏面间的接触采用自动的面面接触运算方法，摩擦采用Coulomb摩擦模型。在闸瓦上按照实际受力分布施加闸瓦压力。建立的闸瓦—车轮三维瞬态热—机耦合有限元模型如图2所示，闸瓦的受力分布如图3所示。

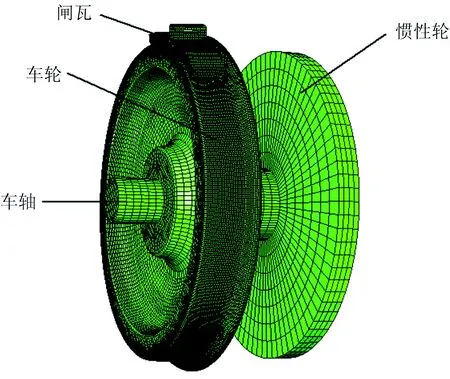
图2 闸瓦—车轮三维瞬态热—机耦合有限元模型

图3 闸瓦的受力分布

车轮和车轴的密度为7 850 kg·m-3，泊松比为0.3，其他材料参数见表1。闸瓦的材料密度为2 500 kg·m-3，泊松比为0.27，弹性模量为500 MPa，热膨胀系数为0.4×10-6℃-1，热传导率为1.12 W·(m·℃)-1，比热为0.9 J·(kg·℃)-1。惯性轮密度根据模拟轮对的轴重不同而不同，其他材料参数与车轮的一致。

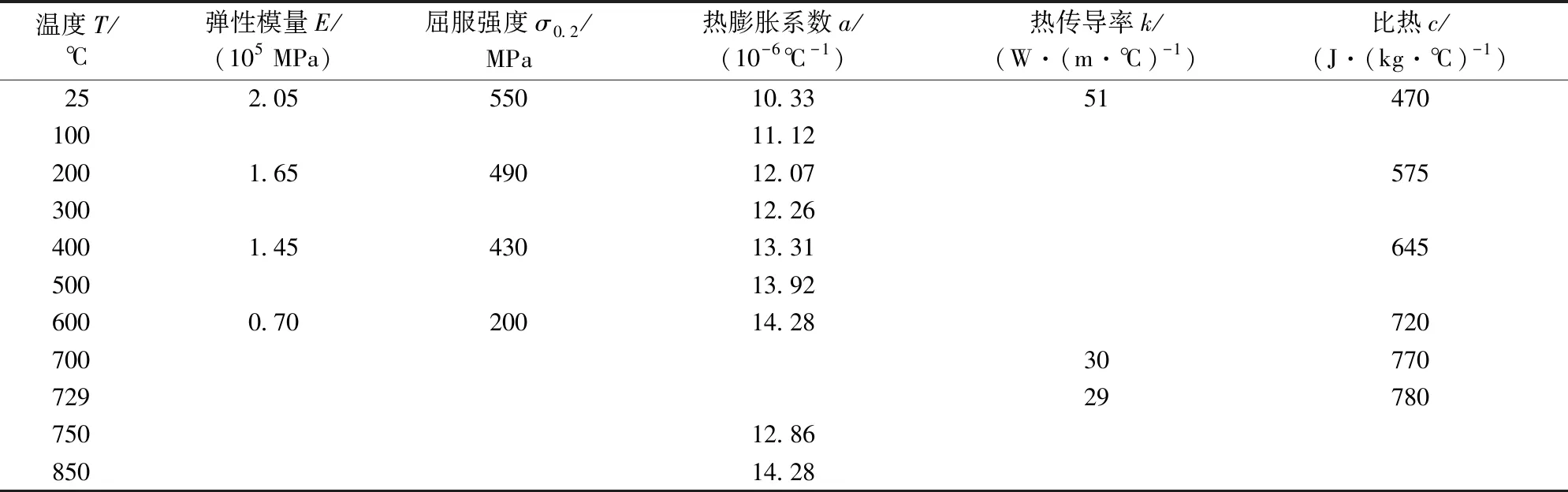
表1 车轮、车轴材料参数

2.2 模型验证

在中国铁道科学研究院集团有限公司国家铁道试验中心制动实验室进行货车车轮踏面紧急制动热负荷试验(如图4所示)。试验主要测试在轴重为23.7 t、闸瓦压力为19.6 kN、制动初速度为120 km·h-1情况下的制动时间和踏面中部最高温度，此时车轮和闸瓦的平均摩擦系数为0.318、踏面初始温度为49.1 ℃。测试结果显示制动时间平均值为59 s，用红外测温仪测得制动时踏面摩擦面中部出现的最高温度平均值为414.6 ℃，最高温度达到446 ℃[6-7]。

图4 制动热负荷试验

采用闸瓦—车轮三维瞬态热—机耦合有限元模型，按照上述试验工况施加载荷和边界条件进行数值仿真分析，得到紧急制动工况下踏面温度及应力的时程变化曲线如图5所示。

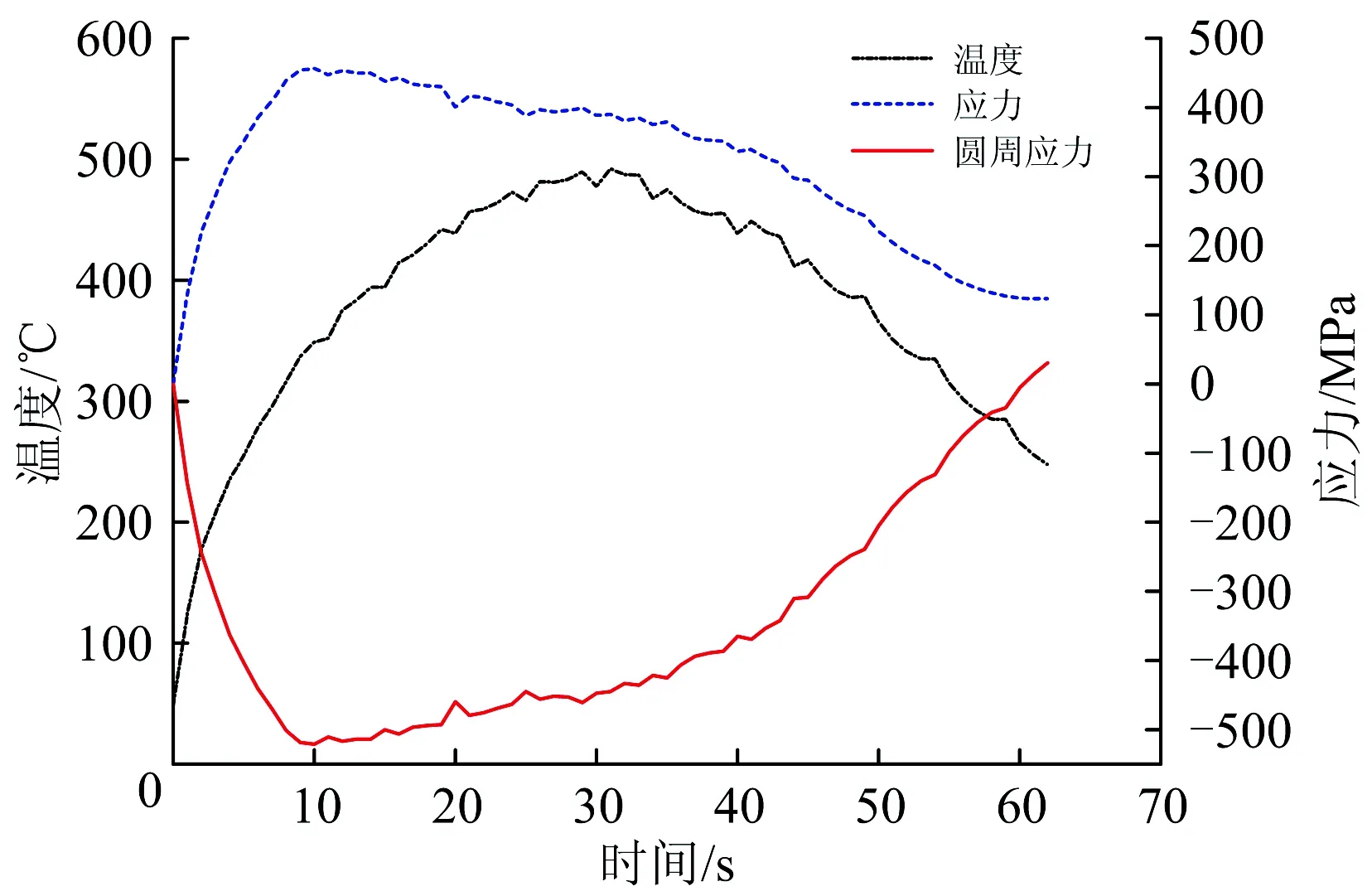
图5 踏面最高温度及应力时程变化曲线

踏面出现最高温度时，踏面的温度分布如图6所示，车轮圆周应力和Mises应力分布如图7所示。

踏面出现最大应力时的温度分布如图8所示。

图6 最高温度时踏面的温度分布

图7 最高温度时踏面的应力分布

由图5和图6可知：在31 s时，踏面温度达到最高，为492 ℃，出现在踏面中部略靠向踏面外侧处，此时踏面摩擦面中间位置的温度为437.4 ℃，与试验得到的最高温度较为一致；仿真结果显示整个制动过程的时间为61 s，与试验结果也非常接近。

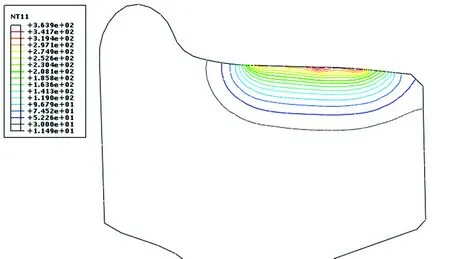
图8 最大应力时踏面的温度分布

从图8可知：在踏面下3 mm范围内，车轮内部温度变化超过了100 ℃，这种较大的温度分布梯度造成车轮圆周应力和Mises应力的增大，超过了最高温度时的应力(图7所示)。

紧急制动试验过程中红外热像仪测得温度分布变化情况与仿真计算温度云图的对比见表2。由表2可知，仿真计算的温度分布变化和试验过程中较为一致；开始时靠近轮缘处的温度较高，然后在轮缘和踏面中间靠外侧处都出现光带，踏面中间的温度稍低，十几秒后，2条光带合在一起，变成了1条光带，最高温度靠近踏面中部偏外侧处；达到最高温度后，温度慢慢降低，光带亮度减弱。

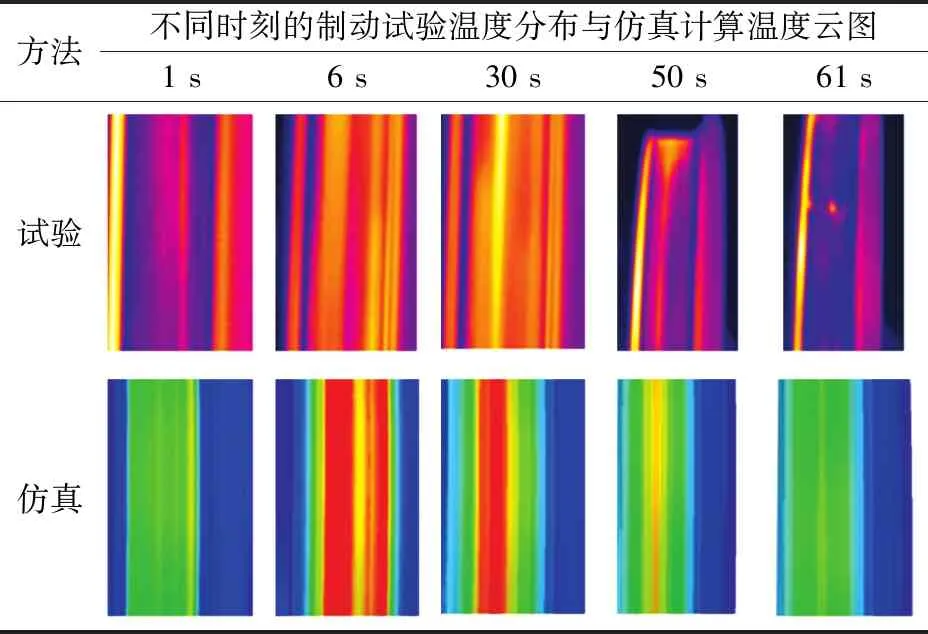
表2 制动试验温度分布与仿真计算温度云图的对比

二维模型通常假设热量在整个车轮踏面上均匀分布，因此车轮最高温度始终出现在闸瓦与车轮踏面接触区的中心，而采用闸瓦—车轮三维瞬态热—机耦合有限元模型可更真实反映车轮与闸瓦实际接触下的温度场和应力场。

3 实例计算

以全长约658 km的大秦线为例，其纵断面如图9所示。由图9可知，大秦线具有2段典型长大下坡道，分别为K140—K190(平均坡度为-0.68%)和K285—K325(平均坡度为-0.95%)区间。

以下选取大秦线K285—K325作为长大下坡道的典型线路，进行循环制动条件下车轮的热负荷和热疲劳裂纹萌生寿命实例计算。

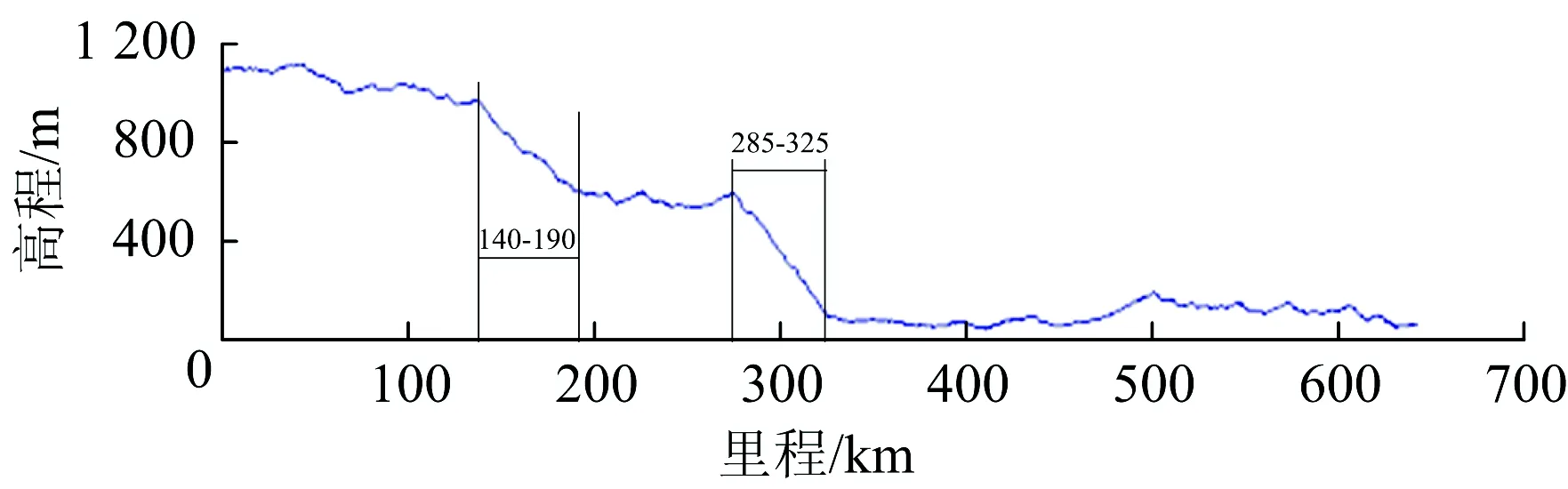
图9 大秦线纵断面示意图

3.1 长大下坡道车轮制动热负荷

采用纵向动力学仿真软件对编组方案为HXD1F型×2辆机车+C80E型×80辆货车、牵引重量为8 480 t的重载货物列车进行制动计算。计算时，列车初速度为75 km·h-1；采用的制动操作策略为电制把位满级，减压量为70 kPa，循环制动4次，第5次制动时由于后面线路限速为45 km·h-1，逐步增大减压量后又实施常用全制动。循环制动的列车运行图如图10所示。

根据纵向动力学计算出列车在长大下坡道时的运行速度和闸瓦压力，采用闸瓦—车轮三维瞬态热—机耦合有限元模型进行重载车轮长大下坡道循环制动热负荷计算，得到车轮踏面温度和Von Mises应力的时间历程曲线分别如图11和图12所示。

3.2 轮轨滚动接触

建立如图13所示轮轨滚动接触应力计算模型，钢轨为75轨，TB60型面；车轮为LM型面。将车轴固定，在轨底施加相当一半轴重的垂向载荷模拟车轮的垂向作用。

3.3 车轮材料的疲劳特性

S—N曲线采用材料拉伸性能参数推导出来的弹塑性应力寿命曲线作应力疲劳分析[8]，即

(1)

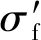
Δε-N曲线采用被广泛使用的Manson-Coffin公式[9-10]，即

(2)

图10 循环制动列车运行图

图11 长大下坡道循环制动时车轮踏面表面温度时程曲线

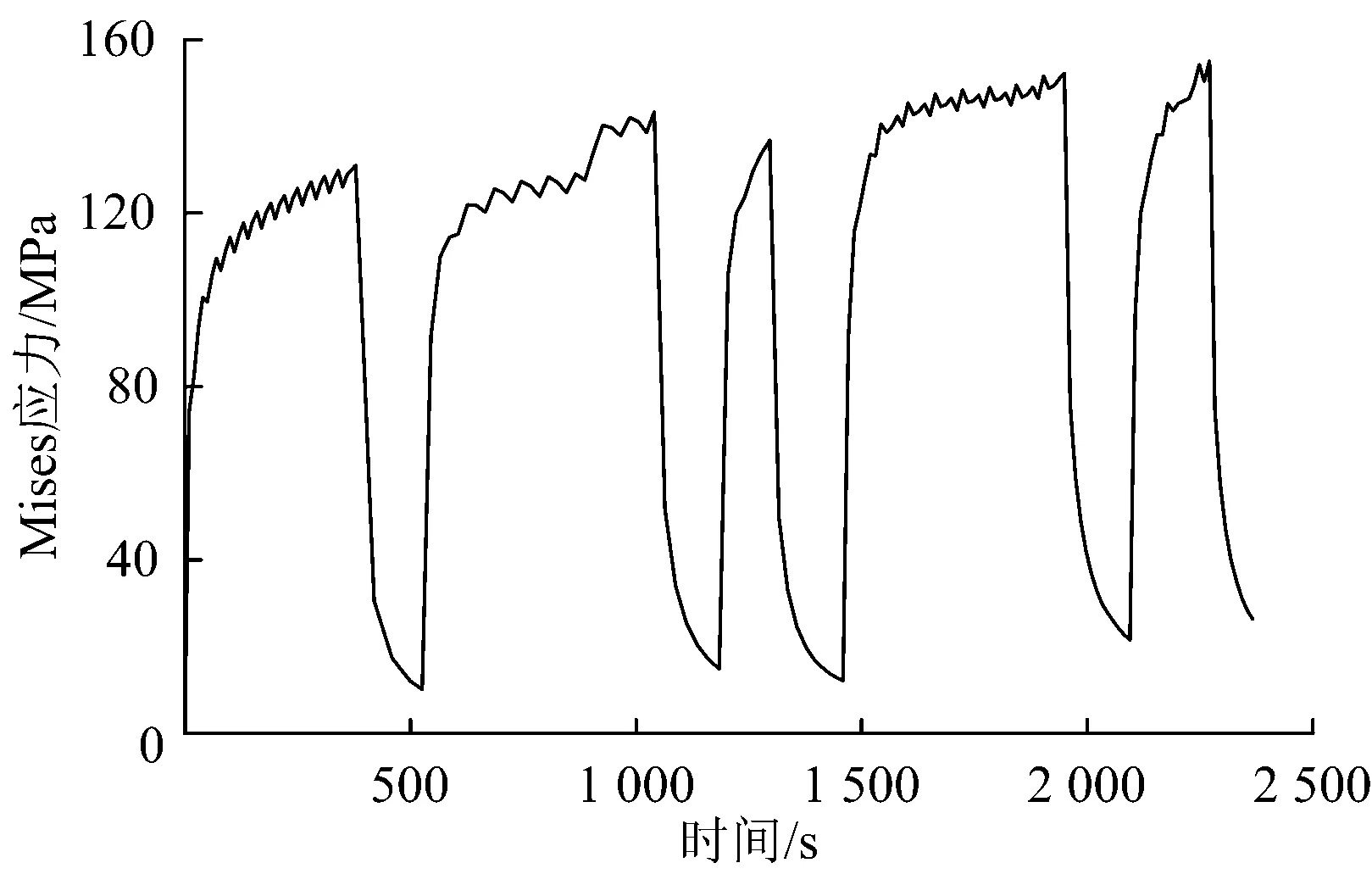
图12 长大下坡道循环制动时车轮踏面Von Mises应力时程曲线

我们站在中国特色社会主义新时代这一历史方位上，要 “立足世情国情党情，统筹推进 ‘五位一体’总体布局、协调推进 ‘四个全面’战略布局”[3]54。全党上下必须遵守党内规章制度、党的纪律、国家法律，尤其是要遵守政治纪律和政治规矩。“我们党是高度集中统一的马克思主义政党，必须始终保持思想上的统一、政治上的团结和行动上的一致。”[3]157增强政治意识、大局意识、核心意识、看齐意识。 “弘扬伟大长征精神，走好今天的长征路，必须把握方向、统揽大局、统筹全局，为实现我们的总任务、总布局、总目标而矢志奋斗；必须加强党的领导，坚持全面从严治党，为推进党的建设新的伟大工程而矢志奋斗。”[3]53-56

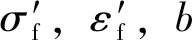
图13 轮轨滚动接触应力计算模型

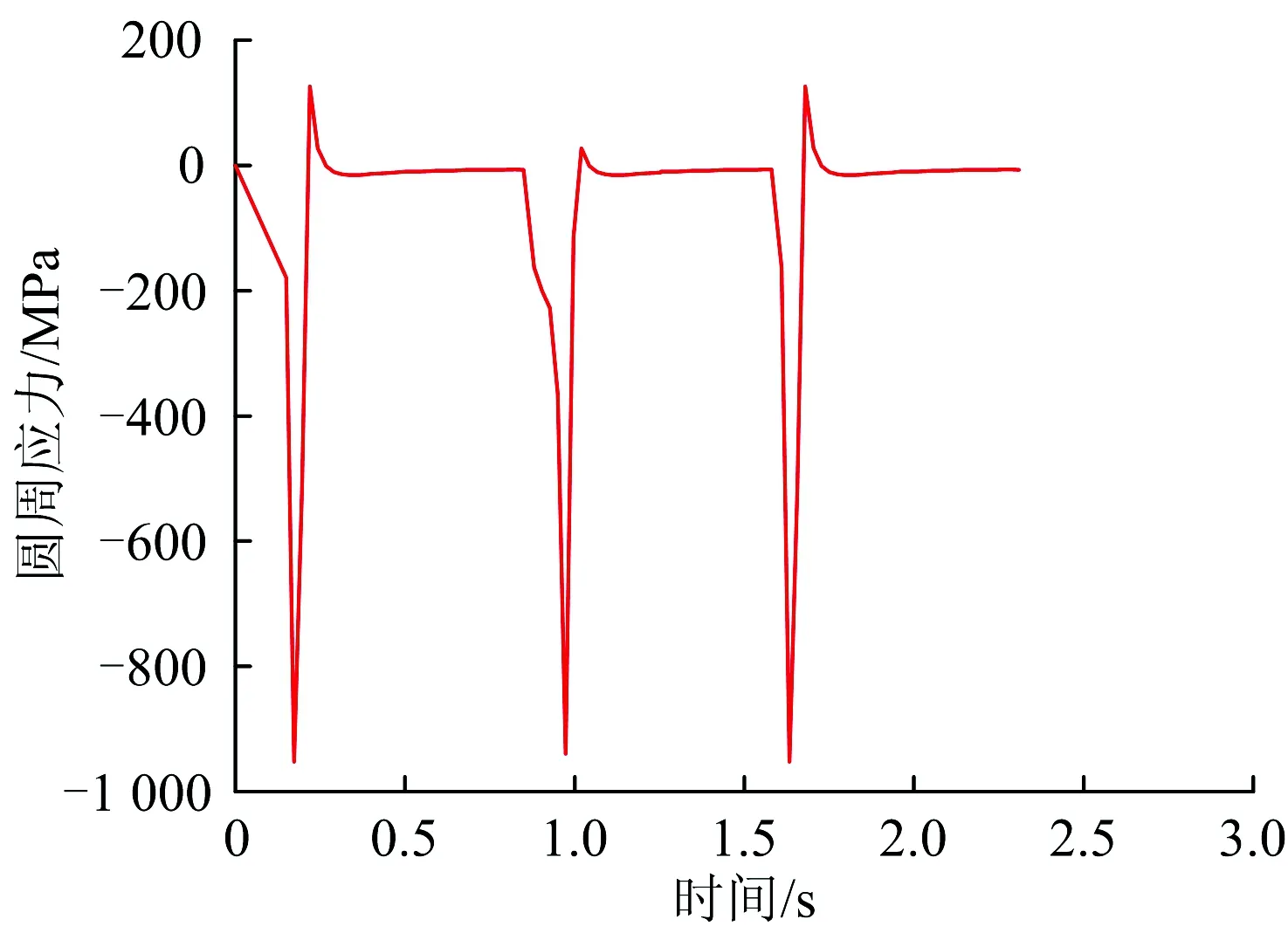
图14 轮轨滚动接触圆周应力时程曲线

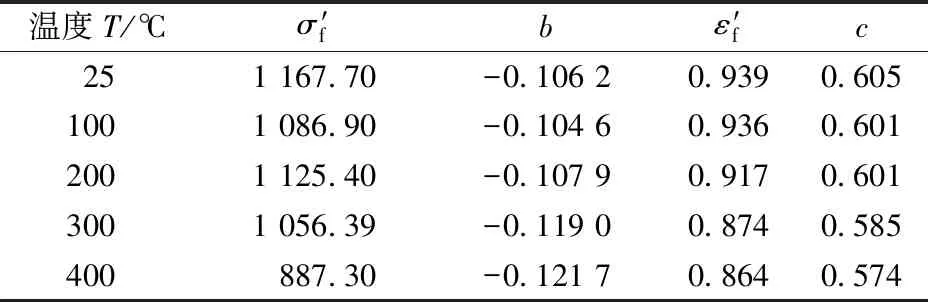
温度T/℃σ′fbε′fc251 167.70-0.106 20.9390.6051001 086.90-0.104 60.9360.6012001 125.40-0.107 90.9170.6013001 056.39-0.119 00.8740.585400887.30-0.121 70.8640.574

3.4 制动热负荷作用下车轮踏面裂纹萌生寿命

由图12可知：长大下坡道循环制动过程中，且仅考虑制动热负荷时，车轮踏面应力水平较低，弹性变形起主导作用，因此可采用名义应力法进行裂纹萌生寿命的计算。

图15 车轮材料在不同温度下的S—N曲线

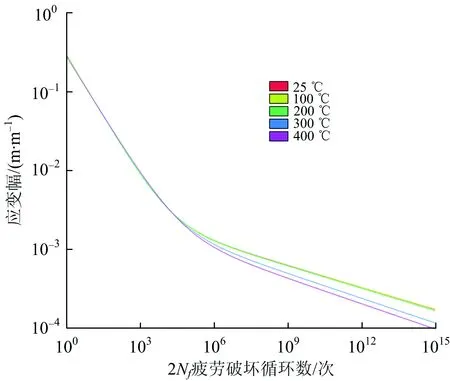
图16 车轮材料在不同温度下的Δε—N曲线

将3.1节得到的车轮热应力时程曲线导入FE-SAFE软件，得到制动热负荷作用下车轮踏面疲劳寿命和损伤结果如图17所示。由图17可见：车轮踏面寿命大于107次时，车轮踏面表面没有出现损伤，说明车轮热负荷单独作用不是导致车轮踏面出现裂纹的主要原因。

3.5 制动热负荷和轮轨滚动接触耦合作用下车轮踏面裂纹萌生寿命

当考虑制动热负荷和轮轨滚动接触耦合作用时，车轮踏面循环应力水平较高，对于裂纹萌生寿命而言塑性应变将起主导作用，因此采用局部应力应变法进行车轮踏面裂纹萌生寿命的计算。

按照图1所示流程，将3.1节计算得到的车轮热应力和3.2节计算得到的轮轨接触应力输入FE-SAFE软件中进行长大下坡道车轮踏面疲劳裂纹萌生寿命和损伤计算，结果如图18所示。

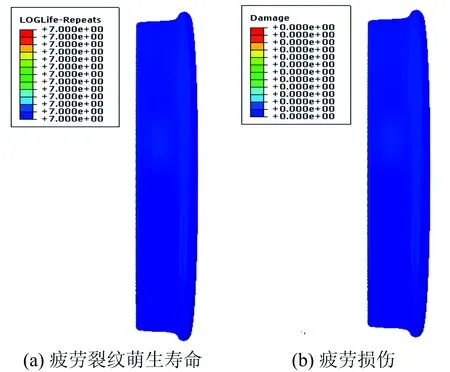
图17 制动热负荷作用下车轮踏面疲劳裂纹萌生寿命和损伤

图18 制动热负荷和轮轨滚动接触耦合作用下车轮裂纹萌生寿命和疲劳损伤云图

由图18可知，车轮在所选长大下坡道上每次循环制动叠加工况的累计损伤最大值为1.34×10-3，计算寿命为745次。按照大秦线上有2段这样的长大下坡道计算，则相当于在大秦线上重车方向运行了373次，即相当于重车方向运行了24.35万km。在考虑常用制动和紧急制动对车轮踏面的损伤后，裂纹萌生寿命的计算结果与现场实际情况吻合良好。

此外，按照长大下坡道约为40 km的距离分别计算了车轮在轮轨滚动接触作用下、踏面温度为恒温200，250，300，350，400 ℃时的损伤和寿命及对应的运行公里数，结果见表4，得到车轮踏面裂纹萌生寿命与温度的关系如图19所示。

由表4和图19可见：在踏面温度低于200 ℃轮轨滚动接触时，车轮踏面未出现损伤，因此轮轨滚动接触载荷单独作用也不是导致车轮踏面出现裂纹的主要原因；在踏面温度达到250 ℃及以上轮轨滚动接触时，车轮踏面出现损伤，且裂纹萌生寿命急剧下降，当踏面温度从250 ℃上升至400 ℃时，裂纹的萌生寿命已经下降了一大半。由图17和图19可见，在不考虑线路条件影响时，坡道制动热负荷或轮轨滚动接触载荷单独作用都不能促使车轮踏面出现损伤形成裂纹，轮轨滚动接触和坡道制动热负荷的耦合作用才是导致此类裂纹萌生的主要因素，其主要原因是坡道制动使踏面温度升高导致材料的性能发生变化，而高频的轮轨接触应力使车轮踏面在高温时出现塑性损伤。

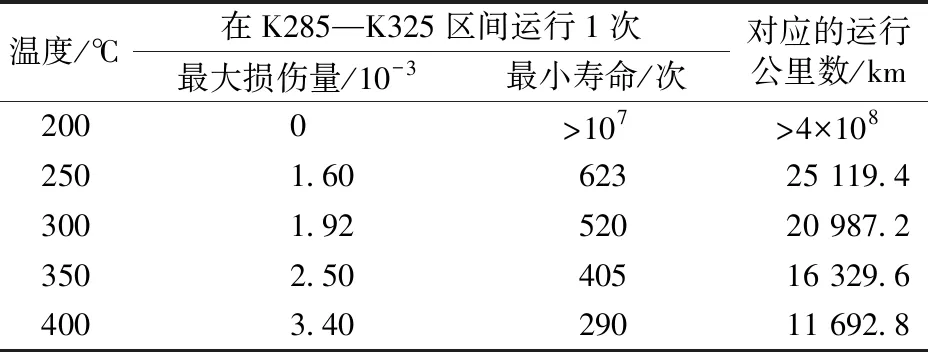
表4 不同温度下车轮踏面裂纹萌生寿命和损伤量

图19 车轮踏面裂纹萌生寿命与温度的关系

4 结 论

(1)综合采用纵向动力学模型、三维瞬态有限元模型和FE-SAFE模型分析了车轮踏面裂纹的萌生寿命，研究表明车轮制动热负荷或轮轨滚动接触单独作用不是导致车轮踏面出现裂纹的主要原因，轮轨滚动接触和坡道制动热负荷的耦合作用才是导致运营车轮裂纹萌生的主要因素。

(2)踏面温度对轮轨滚动接触踏面裂纹萌生寿命的影响非常大，车轮材料采用CL70钢时，温度从250 ℃上升到400 ℃，车轮在长大下坡道裂纹萌生寿命明显下降，对应的运行距离从25 119.4 km下降到11 692.8 km。

(3)制动热负荷和轮轨滚动接触耦合作用下车轮踏面在大秦线K285—K325段每次坡道循环制动的累计损伤最大值为1.34×10-3，计算寿命为745次坡道制动，相当于在大秦线重车方向运行了24.35万km。

(4)在现场运营中，要使车轮和闸瓦保持良好的接触状态，尽可能避免非正常磨耗、非均匀载荷、非正常接触等造成车轮踏面温度的上升，从而减少车轮踏面的损伤，延长车轮的使用寿命。