锥形内表面干涉测量误差分析
黄 欣,吴 鹏,唐寿鸿,韩 森,李雪园,王全召
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;
2.苏州慧利仪器有限责任公司,江苏 苏州 215123;
3.苏州维纳仪器有限责任公司,江苏 苏州 215123)
引 言
锥面作为一种特殊的非球面,它的子午线始终沿着锥面轴线方向。高精度的锥面元件由于自身的特性,可以广泛地应用在测试计量、航天航空、工业加工等领域[1-2]。尤其是在航天航空设计制造领域内,对于零件的平整度、圆柱度、粗糙度等各项指标具有较高的要求。因此,高精度的锥面测量对于精密类轴承的制造和推广尤为重要。
目前,国内锥面元件的测量主要是针对外表面的检测,测量方法主要分为非干涉测量和干涉测量两种。非干涉测量的方法主要有样板法、条纹投影法[3]和接触式测量法。干涉检测的方法主要有掠入射零位干涉测量[4]、计算机全息法(CGH)[5]。
为了能够一次性对回转圆柱内表面的形貌进行高精度检测,孙昊等采用了直角圆锥反射镜,在无拼接的情况下,利用干涉原理,一次性获得了整周被测面的面形[1-2]。本文在此基础上进行了改进,并将其应用于锥面内表面的测量。通过分析误差产生的原因,建立了误差计算公式。
1 测量原理
基于Fizeau干涉仪的回转锥形内表面检测系统原理如图1所示。从干涉仪中射出的光线经分光棱镜之后,一部分光线沿光轴照射到圆锥反射镜上,反射光垂直照射在被测样品表面后,光线原路返回,与另一部分光线发生干涉,产生的干涉图像被CCD所接收。
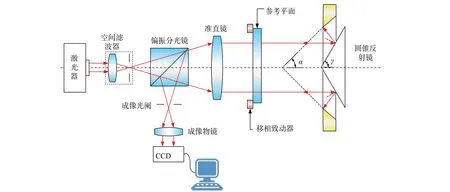
图1 检测系统原理图Fig.1 Schematic diagram of detection system
当圆锥反射镜的顶角和反射表面为理想形状且圆锥反射镜和被测样品均处于理想位置时,干涉图为一个黑白相间的同心圆环图样,如图2所示。
干涉图的光强分布为

式中:It和Ir分别为测试光和参考光的各点光强值; φ(x,y)为相位差; δ为引入的相移量。

图2 干涉图Fig.2 Interference figure

可得到相位差。
2 误差分析
2.1 误差来源
由回转体的特性可知,绕z轴的旋转和沿z轴的平移不会对实验结果产生影响。误差包括:圆锥反射镜垂直z方向产生的偏移误差 Δt;圆锥反射镜顶角加工所产生的角度误差 θ。如图3所示,α为被测表面的倾斜角。
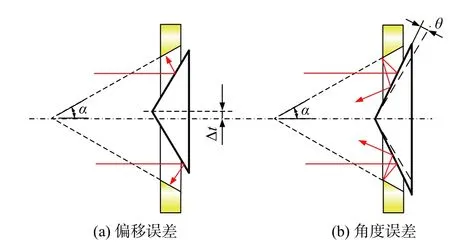
图3 误差产生的原理图Fig.3 The cause of the error
2.2 偏移误差
当圆锥反射镜轴线与被测样品没有相对旋转,仅存在偏移误差的时候,如图4所示。定义在被测表面中过P(R,β,ZP)点且与xy平面平行的截面为,过U点且与xy平面平行的截面为S1,过V点与xy平面平行的截面为S2。其中截面Sp的半径为,截面S1的半径为r1,截面S2的半径为r2。
为了方便计算,可以假设反射镜轴线是沿x轴从O平移了 Δt到O′位置,对于被测样品任意一点P(R,β,ZP)点,其偏移误差的几何光路如图5所示。图中黑色大圆,虚线小圆和黑色小圆分别是截面Sp、截面S1和截面S2在xy平面的投影。其中OP与圆O相交于Q点,O′P与圆O′相交于点B(r2,βB,ZB),其反射光线与圆O′相交于点A(r2,βA,ZA)。
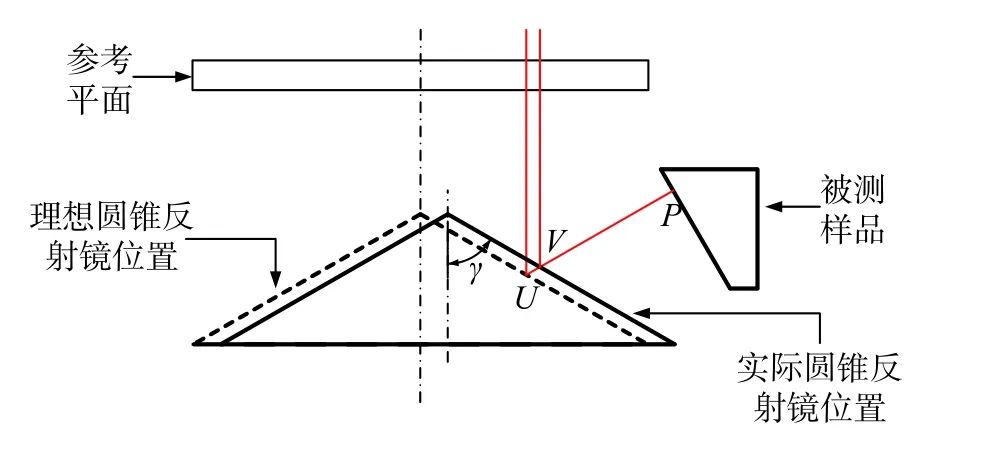
图4 偏移误差示意图Fig.4 Offset error

图5 偏移误差几何光路俯视图Fig.5 Top view of geometrical optical path by offset error
故当圆锥反射镜处于理想位置时,光束打在U点,其对应的投影点为Q,则此时理想光程在xy平面的投影为2QP。当反射镜位于实际偏移位置,实际光路在xy平面的投影则为AP+BP。
故由偏移误差带来的光程差在xy平面的投影为

根据小角度近似和泰勒级数一级展开,通过求解A、B点坐标,有

式中x0为点P在笛卡尔坐标系中的坐标,且x0=Rpcos β(β为被测表面上任意一点P在柱面坐标系中的极角)。

由投影与实际光路的几何关系和式(5)可知,实际光程差为

当圆锥反射镜与被测表面存在偏移误差时,被测表面上任意一点的光程差如式(6)所示。
在实际测量的精调过程中,偏移量极小,根据式(6)绘制出偏移量与光程差的曲线图,如图6所示,其中由图6可知,对于被测面上任意一点P,偏移量与光程差为线性关系。
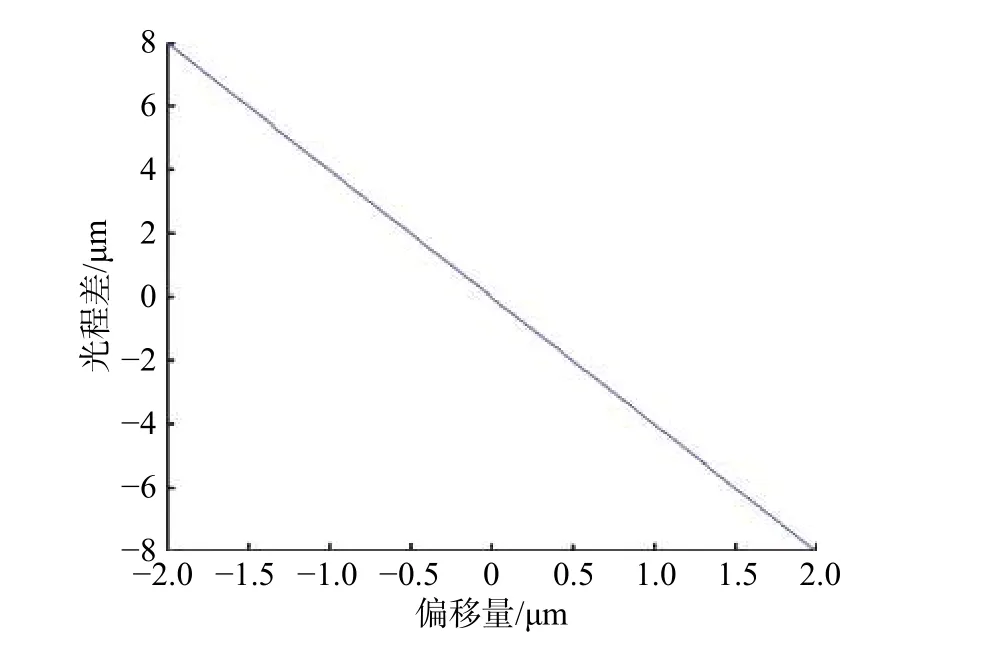
图6 偏移量与光程差的曲线图Fig.6 Relationship between offset and optical path difference
2.3 角度误差
假设反射镜轴线与被测样品轴线都处在理想位置,仅有反射镜顶角存在加工误差,则由角度误差造成的光程差如图7所示。图中虚线三角形表示理想反射镜,实线三角形表示实际反射镜。记参考面到反射镜顶点的距离为s,圆锥反射镜高为hc。图中,点E(rE,βE,ZE)为光线在理想反射镜上的反射点,点F(rF,βF,ZF)和点D(rD,βD,ZD)为光线在实际反射镜上的反射点。
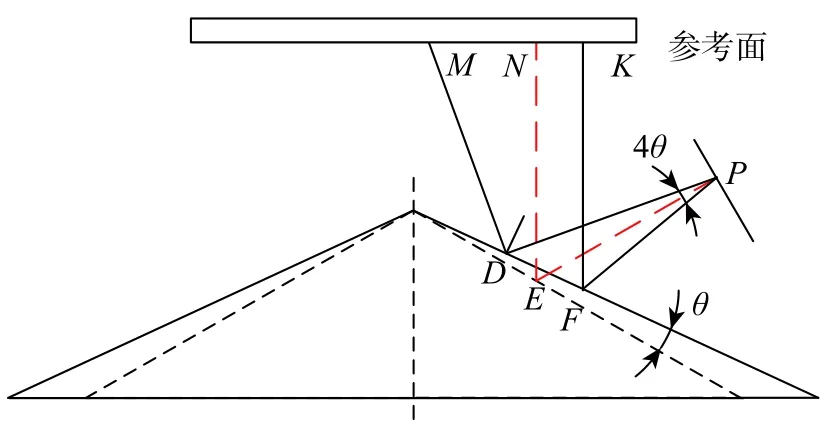
图7 角度误差示意图Fig.7 Angle error
对于被测面任意一点P(R,β,ZP),其光程差为

通过求解D、E、F点的坐标,得到:
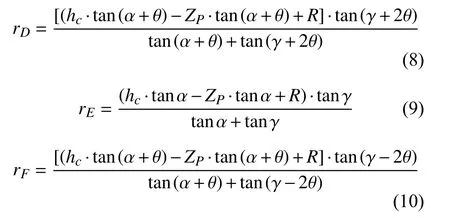
根据几何关系,利用rD、rE、rF可以求得:
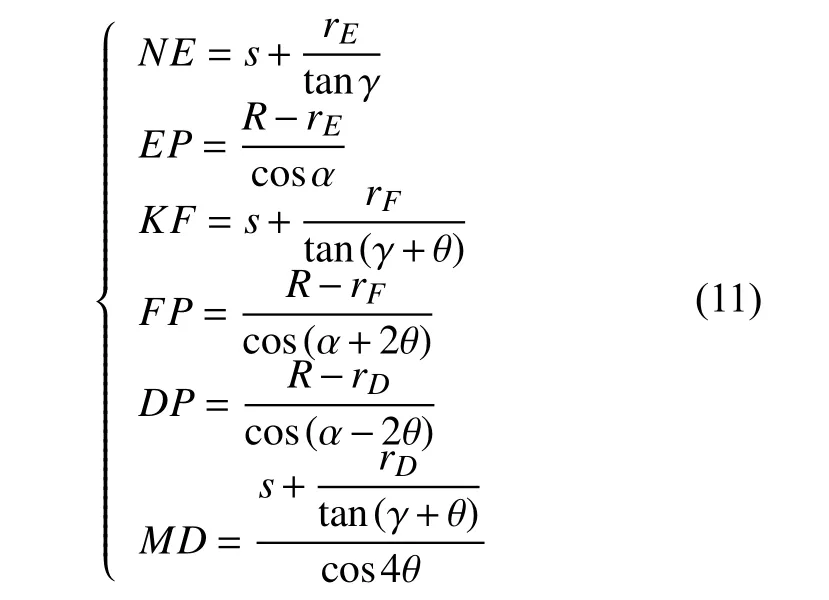
并将式(11)代入到式(7),则有:
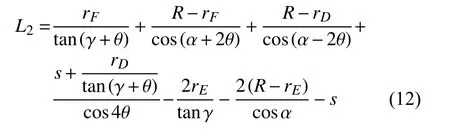
根据式(12),可以绘制出角度误差 θ和光程差L2之间的曲线图,如图8所示,其中令s=200 mm,R=93 mm。
由图8可知,光程差对于角度误差非常敏感。当角度误差超过5′时,光程差已经超过100 μm。当角度误差极小,即在1′以内时,角度误差与光程差近似线性关系。为了保证测量精度,圆锥反射镜的顶角精度需要被严格控制。
3 结 论
本文通过分析误差产生的原因,进行光路追迹,以此构建数学模型,推导出误差计算公式,绘制出光程差与误差的曲线图。研究发现:在圆锥反射镜的偏移量极小情况下,光程差与偏移量成线性关系;光程差对于反射镜的角度误差非常敏感,为了保证实验精度,需要严格控制角度误差的大小。误差计算公式的推导,可为后续利用算法校正误差的研究提供参考。
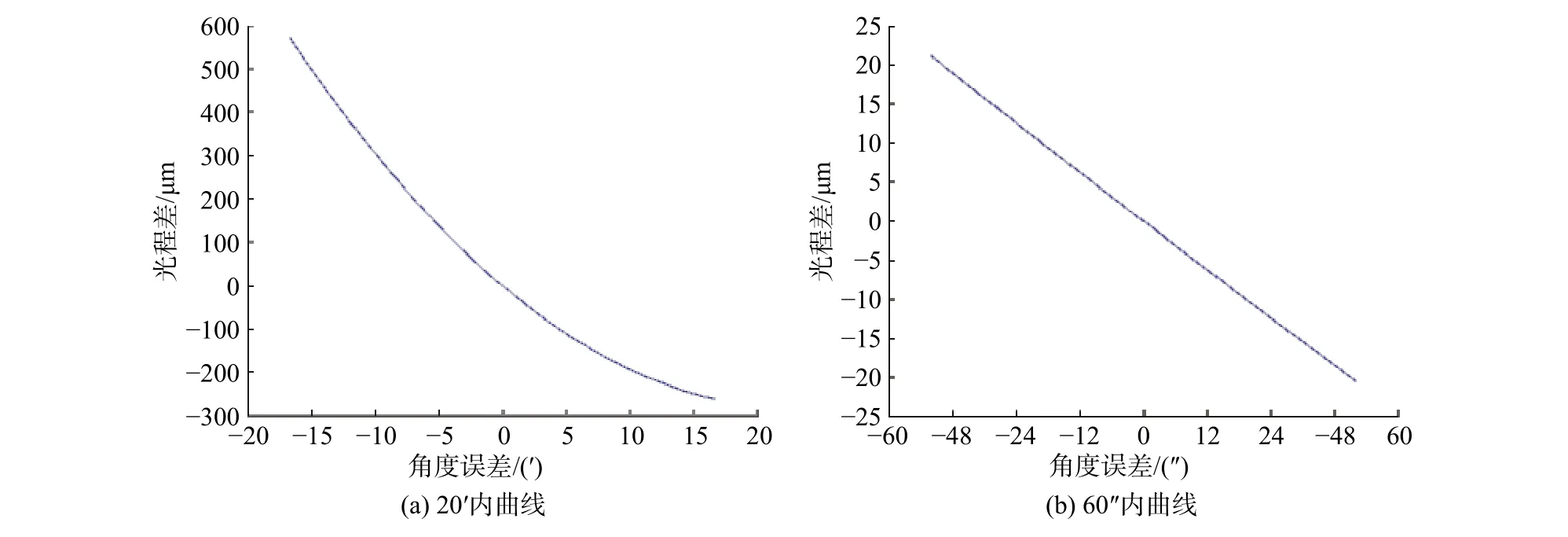
图8 不同的角度误差与光程差曲线图Fig.8 Relationship between the angle error and optical path difference

