散射型近场扫描光学显微镜的探针振动参数优化研究

彭 涛，朱亦鸣，游冠军

（1．上海理工大学 上海市现代光学系统重点实验室，上海 200093；2．上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

随着科技的不断发展，人们对光学显微测量仪器的空间分辨率要求越来越高。扫描近场光学显微镜(scanning near-field optical microscope，SNOM)由于突破了光学衍射极限，能够实现纳米量级的光学成像分辨率，在材料研究、化学分析、生物成像等领域有广泛的应用[1-3]。SNOM利用扫描探针实现了优于半波长的成像分辨率，按照探针有无孔径，SNOM分为孔径式和散射式两类：前者采用亚微米结构的孔径型光纤作为探针，在可见光区能够获得几十纳米到百纳米的成像分辨率，但是波导截止限制了其在中远红外波段的应用[3-4]；后者采用纳米尺寸的散射型探针代替孔径型探针，通常称为散射型近场扫描光学显微镜(scattering-type scanning near-field optical microscope，s-SNOM)[5-8]，由于其光学分辨率和近场信号强度不受激发波长的限制，可广泛应用于可见光-红外-太赫兹宽波段，是近年来国际上纳米光学领域的一个研究热点[9-12]。国内对于s-SNOM技术的研究处于起步阶段，相关报道较少[3]。我们研究组基于原子力显微镜(atomic force microscope, AFM)平台，以 AFM的纳米探针为近场散射探针，设计了可见-近红外波段的s-SNOM，实现了10 nm的光学成像分辨率。

背景散射噪声是影响s-SNOM系统测量性能的重要因素[6-8]，通常采用探针振动的方式对散射信号进行调制，并通过高阶解调从较强的背景散射噪声中提取微弱的近场散射信号，因此探针的振动状态对系统的显微测量性能有重要的影响。本文通过理论模型计算和实验测量，研究分析了探针振动的调制振幅和扫描反馈幅值对近场信号的影响。

1 s-SNOM工作原理

s-SNOM的基本工作原理是通过激发光聚焦照射纳米探针，在探针针尖周围形成增强的局域近场，此局域场与针尖下方的样品耦合，将包含样品信息的耦合近场转化为传播场，因此远场接收的散射光信号中携带了针尖下方样品的光学性质，进而通过探针逐点扫描可获得样品的近场光学显微图像。由于针尖处增强局域场的空间分布尺度主要取决于探针针尖的曲率半径，且不受激发光波长的影响，因此s-SNOM在可见-红外-太赫兹波段皆可实现纳米量级的光学显微测量。

由于激发光聚焦光斑的直径远大于探针针尖的尺寸，远场探测器收集的散射信号中包含被针尖散射的局域近场信号，以及从探针针杆、悬臂梁、样品外部区域散射的远场背景噪声信号，而且近场信号强度远小于背景信号强度，所以s-SNOM的关键技术之一是如何从远场背景信号中提取有效的近场信号。通常采用调制解调的方式获取近场信号，其基本原理是，基于AFM的轻敲工作模式，通过散射探针的轻敲振动(频率为)周期性地改变针尖与样品表面间的距离z，调制针尖散射的近场信号和探针针杆及悬臂梁等区域散射的远场信号。由于随z的增大(减小)，近场隐逝场非线性地迅速减弱(增强)，而背景散射近似线性变化，因此采用高阶解调方式，即以n(n≥2)频率解调，能够从较强的远场散射背景噪声信号中有效地提取微弱的近场信号[6-8]。

为了从理论上描述s-SNOM系统的工作原理，本文采用电偶极子理论模型[7]分析探针针尖与样品之间的近场作用。如图1(a)所示，入射光照射探针和其下方的样品，探针与样品之间的耦合作用可由探针散射元的感应偶极矩与样品中镜像散射元的镜像偶极矩的耦合近似表征。当入射光电场的偏振方向平行于探针针轴时，此耦合系统的总体有效极化率可表示为

式 中 ： β =(εs-1)/(εs+1)， εs为 样 品 的 介 电 常数； α为探针的极化率；a为探针针尖曲率半径；z为探针针尖到样品表面的距离。散射光电场Es可表示为

式中Eo为入射光电场。

假定探针以频率 Ω 、振幅 Δz保持轻敲振动，则针尖-样品之间的距离z随时间的变化为

将式(3)带入式(1)，可以看出探针-样品耦合系统的有效极化率 αeあ(t)在时域上呈周期性变化。

耦合系统的散射信号S大小与针尖的散射截面Csca呈正比。基于Mie散射理论，s-SNOM系统中探针针尖的散射截面为

式中k为入射光波矢的模值。

设激发波长为532 nm，探针针尖曲率半径为20 nm，探针材质为硅，分别计算得到了被测样品为金和硅时探针的散射信号大小，结果如图1(b) 所示。可以看出，金样品的散射信号强于硅样品的散射信号。在近场有效作用范围内，散射信号随样品-探针之间距离的增大呈非线性衰减。与远场散射信号相比，近场信号随探针和样品之间距离的变化更加敏感，因此采用以频率n(n≥2)进行高阶解调的方法，能够有效控制被探针针杆和悬臂梁等部位散射的远场背景噪声。

图1 s-SNOM针尖近场耦合的电偶极子模型及散射信号随针尖-样品间距变化的计算结果Fig. 1 The dipole model of near-field interaction in s-SNOM and the calculated tip-sample distance dependence of scattering optical amplitude

2 实验装置

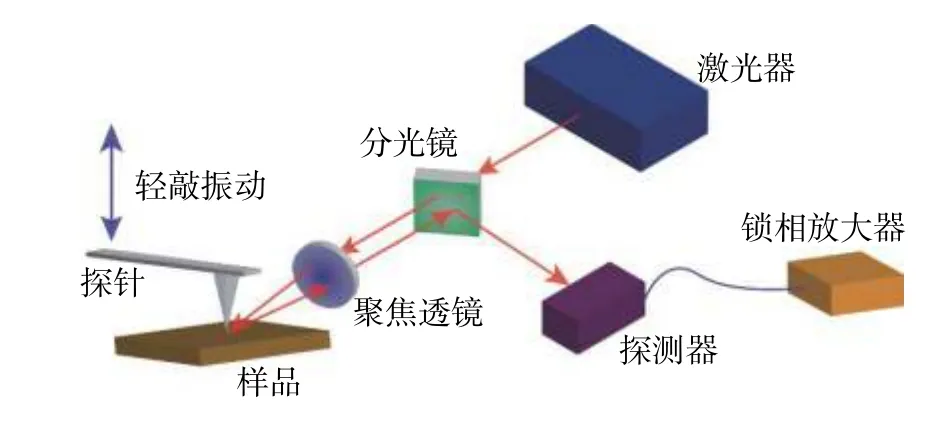
图2 s-SNOM系统结构示意图Fig. 2 The schematic diagram of home-built s-SNOM

本文设计的s-SNOM系统总体结构如图2所示。基于轻敲工作模式的AFM平台，纳米探针以频率振动，照明激光透过分光镜之后被透镜聚焦于探针针尖，背向散射信号被透镜收集，再经过分光镜反射被雪崩探测器接收。探测器产生的光电信号输入到锁相放大器，通过高阶解调从远场背景噪声中提取出近场信号。

3 结果分析

3.1 探针调制振幅对近场信号的影响

探测器接收的散射信号包含了从探针针尖散射的近场信号和从探针针杆、悬臂梁、样品表面散射的远场背景噪声，根据电偶极子理论模型，近场信号和远场背景噪声信号的大小都与探针的振动振幅有关。

为了分析调制振幅对近场信号的影响，分别采用300 mV、600 mV和900 mV的驱动电压驱动针尖曲率半径约为10 nm的AFM探针作正弦振动(=282 kHz)，对应探针在自由空间的调制振幅分别为10 nm、20 nm和30 nm，解调频率设置为，测量探针针尖逐渐靠近金膜表面时散射信号的三阶解调幅值S3，结果如图3(a)、(b)所示。

图3 不同调制振幅下的s-SNOM三阶解调信号Fig. 3 The 3demodulated optical amplitude under different modulation amplitude

从图3(a)可以看出，在针尖-样品表面间距为0～25 nm时，信号幅值随间距增大而非线性地快速衰减，这与前文计算结果相符。信号分布的空间范围与针尖尺寸也很好地相符，说明此处提取的信号来源于局域的隐逝近场。归一化后的结果如图3(b)所示，在近场作用范围内(间距≤25 nm)，不同调制振幅下的数据曲线互相重合，说明调制振幅不影响近场测量的分辨率。在远场区域(间距≥50 nm)，当调制振幅≤20 nm时背景噪声信号幅值接近零，而当调制振幅增大到30 nm时，背景噪声信号随针尖-样品间距增大呈振荡增强趋势。此结果说明，当调制振幅大于针尖尺寸时，背景噪声抑制效果变差，这会影响到系统的近场测量性能，如显微成像的对比度。测量时设置与针尖尺寸相近的调制振幅，可以有效地抑制背景噪声，获得较高的信噪比。

3.2 扫描反馈幅值对近场信号的影响

s-SNOM通过探针逐点扫描样品获得近场显微成像，扫描样品时的探针振动状态与在自由空间时有所不同。当探针距离样品表面较远时，探针和样品间的相互作用力非常弱，可近似忽略不计，探针在共振频率点(或附近)做简谐振动。当探针接近样品表面时，其与样品之间的相互作用力导致振动偏离简谐模式，因此含有频率为n(n≥2)的非简谐成分[13-15]。由s-SNOM散射信号的调制和解调机制可知，探针振动的简谐性会影响背景噪声的过滤和近场信号的提取。如果探针振动的非简谐成分较强，背景散射噪声中也含有n频率成分的调制，导致高阶解调无法有效地过滤背景噪声，因此影响s-SNOM显微测量的性能。为了进一步了解探针振动状态对近场测量的影响，本文通过设置不同的扫描反馈幅值(setpoint)，研究了探针扫描振幅对近场显微成像的影响，实验测量结果如图4所示。

被测样品为厚度50 nm的粗糙金膜，表面起伏度约为5 nm，探针在自由空间的调制振幅设为16.5 nm，系统采用三阶解调模式提取近场散射信号。图 4(a)、(b)、(c)为 AFM形貌图，(d)、(e)、(f)是与(a)、(b)、(c)对应的近场光学显微图，扫描反馈幅值As分别设置为14.3 nm、14.9 nm、15.5 nm。图4(d)中分布着较多的深色短线条，虚线圆圈内是典型的短线条。这些短线条是与表面形貌相关的假信号[6]，与图4(a)对比可以看出，假信号主要位于表面高度起伏较明显的区域。当增大探针扫描反馈幅值(≥14.9 nm)时，如图4(b)和(c)所示，近场显微图中的假信号基本消失。此结果说明，如果探针扫描反馈幅值过小(小于自由空间调制振幅的90%)，探针扫描过程中与样品的相互作用力较强，易出现非简谐的振动状态，导致产生与表面形貌相关的假信号。为了获得真实准确的近场信号，探针的扫描反馈幅值应大于其自由空间调制振幅的90%。

图4 金膜样品的形貌图与近场光学显微图Fig. 4 The topography and optical amplitude images of gold thin film

3.3 s-SNOM近场显微成像测试

对探针振动的调制振幅和扫描反馈幅值进行优化后，测试了本文设计的s-SNOM系统的显微成像性能。照明激光波长为532 nm，被测样品为电子束蒸发制备的金膜，选取表面附着了较多纳米尺度杂质颗粒的区域进行测试，结果如图5所示。图5(a)为AFM形貌图，(b)为三阶解调的近场光学显微图，(c)为对应于(a)和(b)中虚线的剖面图。图5(b)中杂质颗粒边界清晰，与AFM形貌图中显示的杂质分布一一对应。近场光学显微图具有较好的对比度，其中杂质区域的近场信号显著减弱，这与之前的报道相符[16]。杂质颗粒的高度约为8～10 nm，虽然杂质边界处高度落差较大，但没有出现与形貌相关的假信号。分析图5(c)中的剖面数据，得出s-SNOM系统的显微成像分辨率约为10 nm。

图5 s-SNOM系统测试结果Fig. 5 s-SNOM images of gold thin films and impurity nanoparticles

4 总 结

本文主要研究了s-SNOM系统中探针振动的调制振幅和扫描反馈幅值对显微成像性能的影响。研究表明：当调制振幅与探针针尖尺寸相近时，有利于抑制散射信号中的背景噪声，提高系统成像的对比度；较小的扫描反馈幅值会导致近场信号中包含较多与样品形貌相关的假信号，因此为了获取被测样品的真实近场信号，需设置探针的扫描振幅大于其在自由空间调制振幅的90%。