列车主动悬架液压放大GMA系统振动控制仿真研究

孟建军，何昌雪，李德仓，胥如迅

（1.兰州交通大学 机电工程学院，兰州 730070；2.兰州交通大学 机电技术研究所，兰州 730070；3.甘肃省物流及运输装备信息化工程技术研究中心，兰州 730070）

0 引言

轨道交通客运量的不断增长，促使列车运行高速化成为铁路交通领域发展趋势[1]。随着列车运行速度的不断提高以及高强轻型车体结构技术的发展，导致列车在运行过程中振动加剧，传统的悬架系统难以满足减振性能要求[2,3]。超磁致伸缩作动器（GMA）具有响应快速、输出作动力大以及磁机耦合系数高等诸多优点[4]，被广泛应用于振动控制系统中[5]。采用GMA系统作为列车主动悬架力作动器成为研究的新方向。现有的技术条件下，GMA主要应用在微控制领域，想要达到明显减弱和抑制列车振动的效果，则需要对GMA的输出位移进行放大。

目前，液压型位移放大机构常用于对GMA系统的输出位移进行放大[6]。本文设计的液压位移放大机构，安装于GMA输出端，配合GMA一起工作，将GMA核心部件超磁致伸缩棒（GMM）在驱动磁场作用下产生的输出位移放大。与柔性铰链等机械位移放大机构相比，液压位移放大机构易于设计安装，应用场合广泛，可以很好的与GMA系统耦合[7]。

本文采用液压放大机构实现GMA系统输出位移的放大，产生主动悬架减振所需的位移和作动力，克服GMA系统输出位移较小的不足，充分发挥GMA系统的优越性能。验证了GMA系统应用于列车主动悬架振动控制的可行性和合理性，为实际工程应用提供一定参考。

1 液压位移放大器结构设计

帕斯卡定律是流体力学中液压位移放大的最基本原理，即密闭液体上的压强在各个方向上处处相等，静压力向液体介质的各个方向传递[8]。利用帕斯卡原理，设计液压位移传动系统，原理如图1所示。

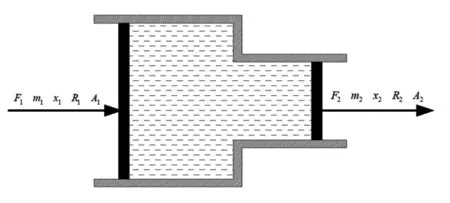
图1 液压位移放大机构原理图

该机构主要由大小两个膜片和一个充满液体介质的密闭容腔组成，外力F1作用在在大膜片端，使大膜片形变产生位移x1，推动小膜片向右移动输出力F2和位移x2。考虑稳态工作，忽略液体介质的泄露及可压缩性影响，得到严格的传动比，满足：

放大机构放大倍数：

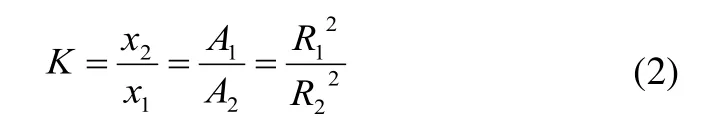
此外，油液各处压强相等，故：

放大机构输出力：

基于以上原理可知，液压传动系统不能同时实现位移和输出力的放大，在实际应用时必须根据具体场合和控制要求，选取合适的放大倍数，保证输出力与位移都满足工作要求。根据以上分析，结合GMA结构和主动悬架应用场合，设计能平稳传动、快速响应的的液压位移放大器，具体结构如图2所示。

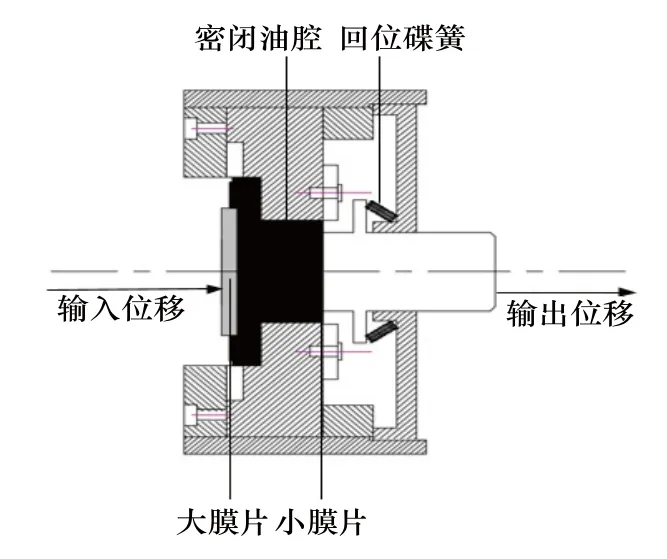
图2 液压位移放大器的结构

2 GMA结构设计及动力学模型

2.1 GMA结构设计

GMA结构设计主要围绕GMM棒展开，首先依据系统控制性能要求确定GMM尺寸结构，再设计GMA整体外形与结构，最后对GMA内部的各个部件进行优化[4]。图3为GMA结构设计简图[9]。

如图3所示，GMA系统工作时，驱动线圈在外部能源激励下提供驱动磁场，需根据主动悬架减振参数合理设计驱动线圈的匝数、线径以及驱动电流的大小和频率，使GMA输出作动力能够满足主动悬架减振要求；为避免非线性作动力和消除倍频现象[16]，需要偏置线圈施加偏置磁场，用来保持GMM棒在线性区工作，减小GMM棒动态响应的不灵敏区，获得较高的机电耦合系数和实现同频率的机电能量转换；理论分析和实验均表明，使GMM棒始终处于压应力状态下，GMM棒磁致伸缩特性将会有很大提升，产生更大的伸缩应变，在此设计拧紧螺母和预紧弹簧，使预紧力可以在一定范围内调节；由于GMA工作性能易受到温度变化的影响，为了使作动器在最佳温度下工作，在GMA设计时，一方面对驱动线圈功率进行优化尽量减少发热，另一方面设计冷却装置保证GMA系统的稳定性及可靠使用。

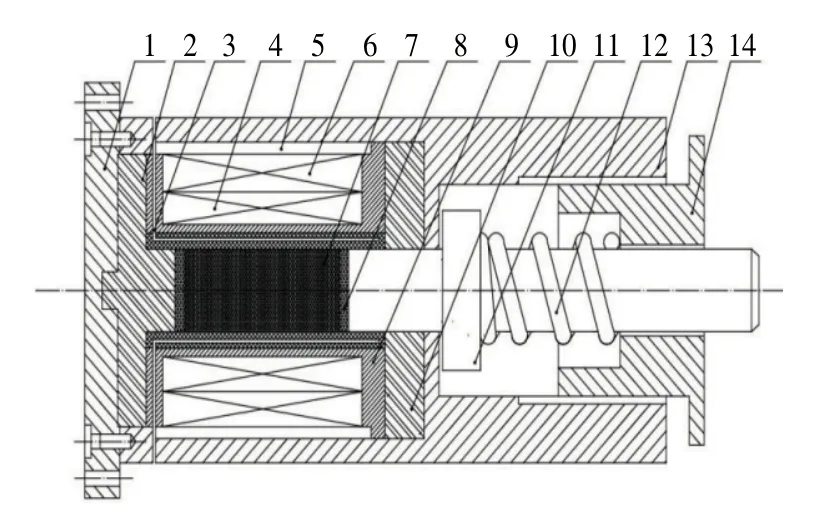
图3 GMA结构设计图

GMA结构设计通常分为两个阶段，首先是依据预期输出位移、作动力和带宽等确定GMA机械结构和外部形状等主体结构。第二阶段为结构与参数的优化、初始状态及偏置条件的设定，以及对冷却装置等进行设计，优化GMA性能，最后确定GMA结构主要参数[4]，如表1所示。

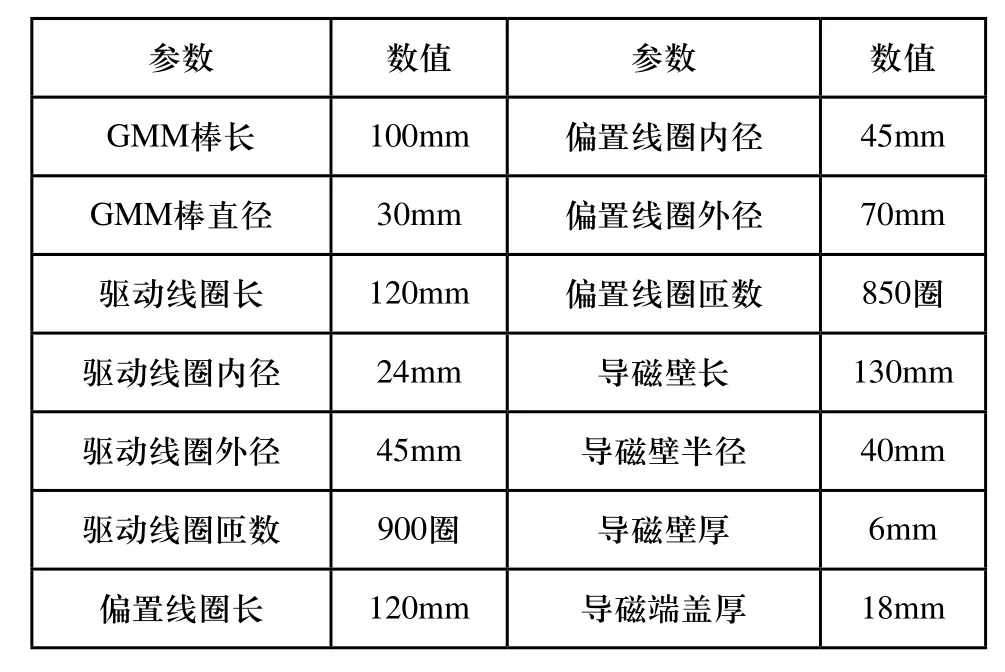
表1 GMA结构主要参数

2.2 液压位移放大GMA结构设计

本文采用GMA系统作为列车主动悬架减振作动器，实现列车振动的有效抑制。针对GMA固有特性造成的作动器输出位移有限的情况，设计与之耦合的液压位移放大机构，如图4所示。

位移放大器结构大膜片端与GMA的非导磁输出杆相连接，在驱动线圈作用下GMA产生磁致伸缩效应，输出位移与作动力，施加在放大结构的大膜片端，经过密闭油液传动，在小膜片端放大GMA的输出位移。所设计的液压位移放大器结构紧凑、承载力大，可以很好的与GMA结构相耦合，放大输出位移，满足列车主动悬架实际应用的需求。

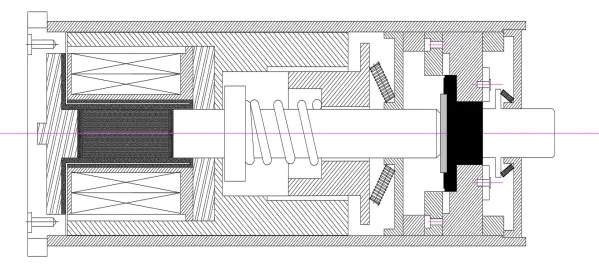
图4 液压位移放大GMA结构

2.3 GMA系统动力学模型

针对液压位移放大GMA系统的动力学特性，根据超磁致伸缩材料机电耦合特性，采用等效的方法，将GMA系统的磁致伸缩效应转化为等效力，建立GMA振动动力学模型。在推导GMA系统等效动力学模型时，作如下假设[10,11]：

1）GMM棒长度与驱动线圈一致，通入驱动电流后，GMM棒内部磁感应强度B、磁场强度H、应变ε和应力σ认为均匀分布。其中，GMM棒输出位移 y =εlr，输出力 F =σAr，lr、Ar分别为GMM棒长度和横截面积；

2）考虑施压连接刚度，认为负载（包括车体和转向架架构）是质量-弹簧-阻尼型负载；

3）在GMA工作过程中，GMM棒一端与转向架架构固定，另一端与负载同步运动，输出相反的位移与作动力。

基于以上假设，将GMA的动力学过程简化为等效单自由度动力学模型，如图5所示。

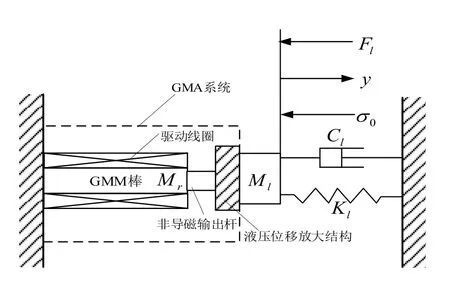
图5 GMA等效动力学模型

设N、ls、I分别为驱动线圈的匝数、长度和控制电流；设lr、d、Ar、ρ、Kr、Mr分别为GMM棒的长度、直径、横截面积、质量密度、等效阻尼系数、等效质量；设Ml、Cl、Kl分别为负载的等效质量、等效阻尼系数、等效刚度系数；F、y、σ0分别为GMM棒的输出作动力、位移和受到预紧装置提供的预应力；Fl为负载对GMM棒的作用力。

基于GMM棒特性的应变方程为：

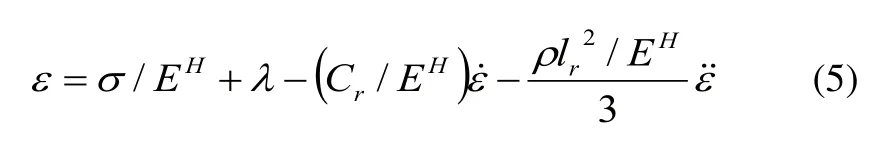
式(5)中λ为考虑磁滞的磁应变，EH为GMM棒在长度方向的杨氏模量。

基于第3个假设，外部负载对GMM棒的作用力为：

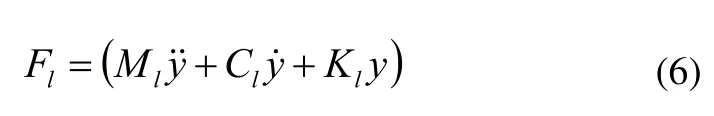
考虑到GMM棒受到预紧弹簧的预应力σ0，则GMM棒输出力为：

联立式(5)和式(7)，可得在λ和σ0作用下，GMA系统的动力学微分方程为：

其中：M=Mr+Ml，Mr=ρlrAr/3

对式(8)取拉氏变换，s为Laplace算子，得到GMA系统输出位移为：

GMA系统输出作动力Fs与Fl数值相等，方向相反，对式(6)取拉氏变换得：

由式(10)可得GMA系统输出力力Fs到输出位移y的传递函数GFs-y为：

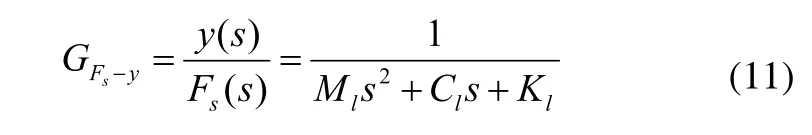
联立式(9)和式(10)，可得GMA系统输出力为：

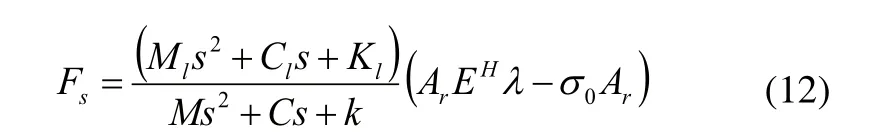
最终建立的GMA动力学模型基本参数如表2所示。

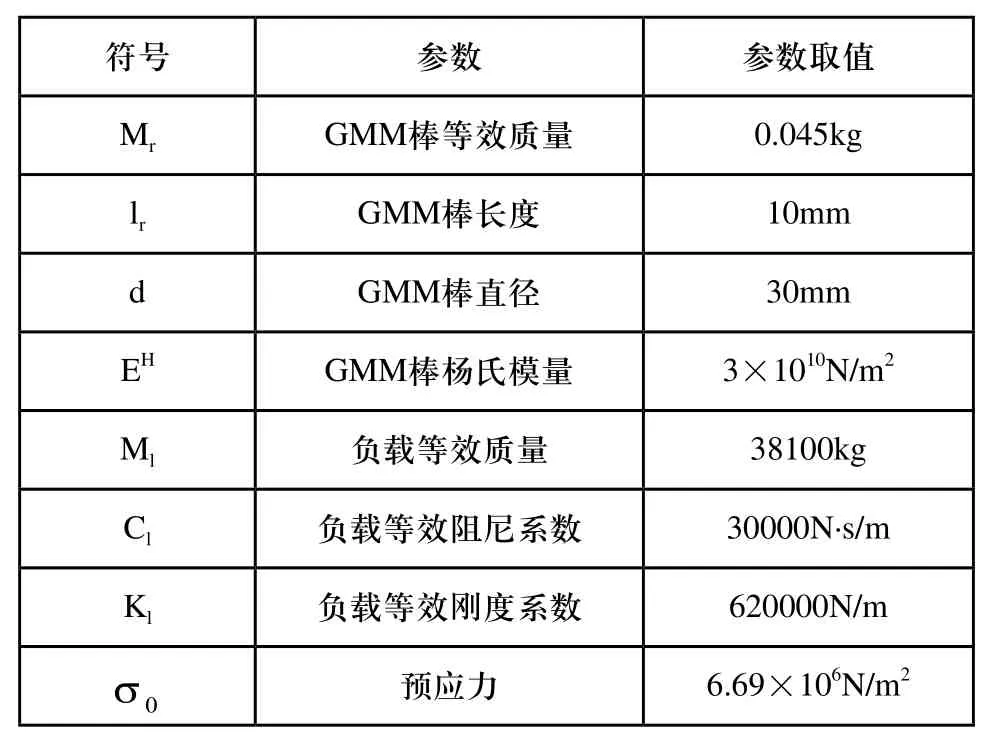
表2 GMA动力学模型基本参数

3 GMA主动悬架动力学模型

列车主动悬架主要由外界能源输入，作动器，测量传感系统和反馈控制系统几部分组成，是闭环的反馈控制系统[12]。测量传感系统获取列车实时运行状态，控制器经算法计算得到合适的悬架控制参数，作动器在控制器设计好的作动参数下产生控制力，在不同的运行车况下都能达到最佳抑振效果。

参考最常采用的车辆悬架控制系统经典模型[13,14]，本文将GMA系统列车主动悬架简化为1/4车辆二自由度动力学模型，如图6所示。

图6 1/4车辆二自由度主动悬架动力学模型

图6中：Mw为轮对质量；Mt为转向架架构质量；Mc为车体质量；Kw为一系悬架弹簧刚度；Ks为二系悬架弹簧刚度，Cs为二系悬架阻尼系数；Fs为GMA系统作动力力；Zs和Zt分别为车体和转向架架构的位移；Xr为轨道不平顺等外部激励。

分别对车体和转向架架构质量进行力学分析，根据拉格朗日方程推导得到系统动力学方程如下：

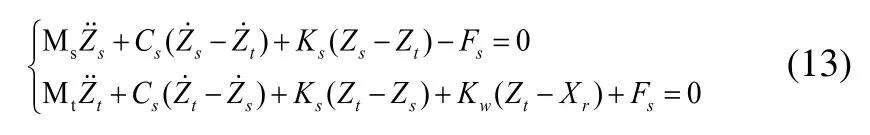
令z1=Zt；z2=Zs；k1=Kw；k2=Ks；m1=Mt；m2=Ms；c=Cs；f=Fs；u=Xr，则式(13)简写为：

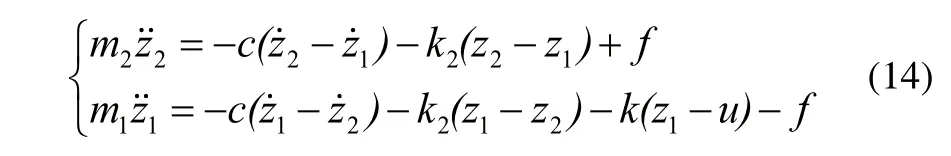
式(15)中输入向量U=（f，u），解得A，B，C，D分别为：

4 数据仿真分析

为了验证主动悬架液压放大GMA系统振动控制效果，根据前文所建的GMA系统动力学模型以及1/4车辆二自由度主动悬架动力学模型，利用Matlab-Simulink仿真软件搭建GMA系统仿真模型和主动悬架仿真模型，如图7和图8所示。

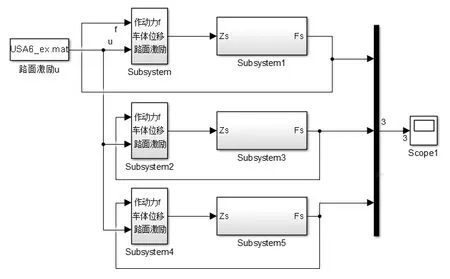
图7 GMA系统Matlab-Simulink仿真图

图8 主动悬架Matlab-Simulink仿真图

上述仿真模型中物理量参考某典型列车部分参数[15]，具体参数数值如表3所示。

表3 主动悬架模型物理量参数

4.1 GMA系统对车体响应的影响

为了验证GMA系统用于列车主动悬架的减振效果，以1/4车辆二自由度被动悬架和主动悬架为仿真对象，以美国六级轨道高低不平顺作为外部输入激励，利用Matlab-Simulink分别对被动悬架和GMA系统主动悬架进行数据仿真，得到以200km/h速度运行时的列车车体响应（车体浮沉振动位移、车体浮沉振动速度、车体浮沉振动加速度），结果如图9与图10所示。

图9 被动悬架车体响应

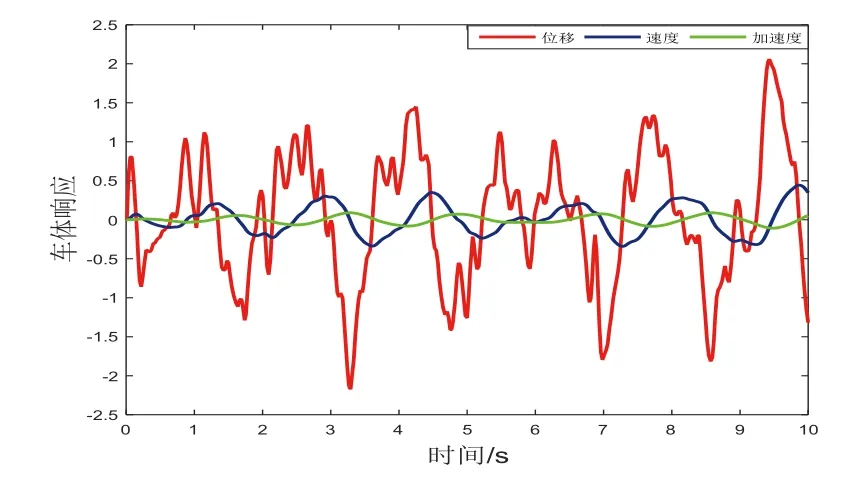
图10 GMA系统主动悬架车体响应

为了更直观得到GMA系统对车体响应的影响，分别仿真被动悬架和GMA系统主动悬架的不同车体响应，结果如图11～图13所示。将两种悬架减振性能进行对比分析，得到GMA系统控制前后车体振动响应最大幅值参数如表4所示。

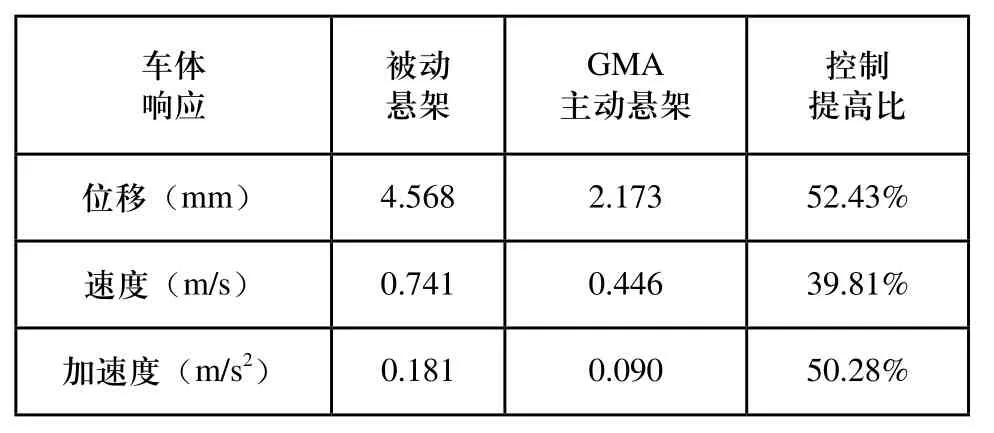
表4 GMA系统控制前后车体振动响应对比

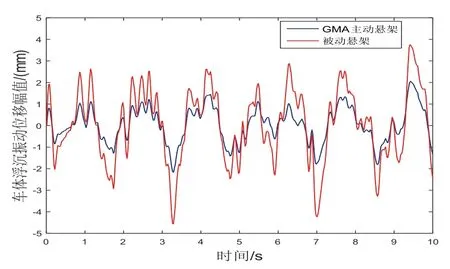
图11 车体浮沉振动位移-时间响应

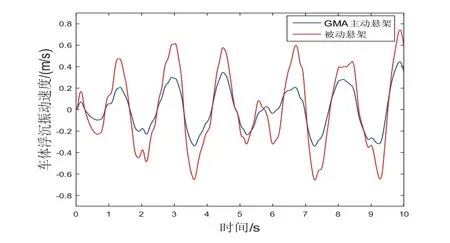
图12 车体浮沉振动速度-时间响应

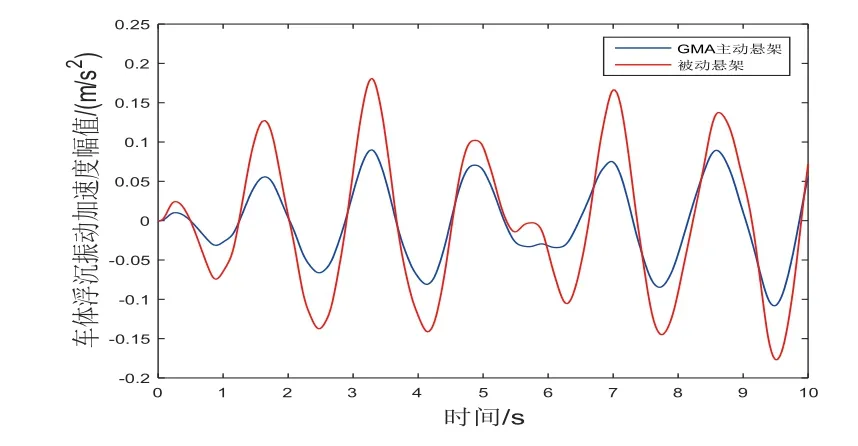
图13 车体浮沉振动加速度-时间响应

从图11～图13可知，GMA系统主动悬架要比被动悬架的减振效果优越。具体的，由表4的分析结果可知，相比于被动悬架，GMA系统主动悬架的车体浮沉振动位移幅值、速度和加速度幅值均明显减小，振动控制效果分别提升了52.43%、39.81%和50.28%，其中车体浮沉振动最大位移幅值从4.568mm减小到2.173mm，实现了更佳的振动控制性能。

4.2 不同放大倍数对GMA作动力的影响

通过对1/4车辆二自由度主动悬架动力学模型进行数据仿真，可以得到GMA系统用于主动悬架减振时的理想输出作动力，结果如图14所示，理想作动力幅值最大约为3800N。

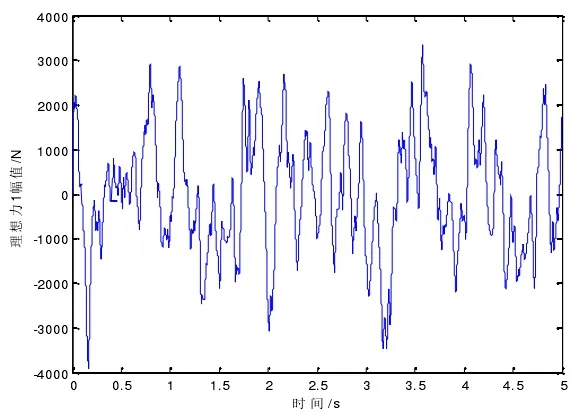
图14 GMA理想作动力幅值-时间响应

由液压位移放大机构的工作原理可知，位移放大机构在放大GMA输出位移的同时会导致输出力减小，因此必须选择合适的放大倍数，使GMA系统同时满足主动悬架对作动器输出位移和减振力的要求。在Matlab仿真过程中，对模型参数进行设置，位移放大倍数最大取10倍，仿真结果如图15所示。

由图15可以看出，不同位移放大倍数直接影响GMA输出作动力的大小，随着位移放大倍数的增加，GMA输出作动力持续减小。当放大倍数为3倍时，GMA输出作动力幅值最大约为3200N；当放大倍数为5倍时，GMA输出作动力幅值最大约为1900N；当放大倍数为10倍时，GMA输出作动力幅值将减小到1100N，已经无法达到主动悬架系统减振所需的控制力。

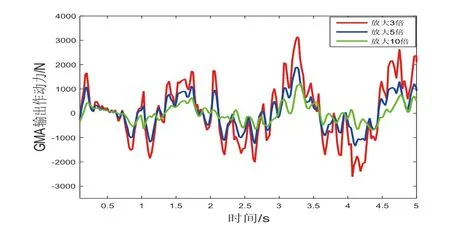
图15 不同放大倍数GMA作动力幅值-时间响应

5 结论

1）在分析GMA工作原理的基础上，针对列车主动悬架具体应用场合，设计了具有液压位移放大机构的GMA作动系统，并应用到列车的振动控制。

2）建立了GMA系统动力学模型和主动悬架动力学模型，仿真验证了GMA系统用于主动悬架的可行性和优越性。与被动悬架相比，GMA系统主动悬架可以大大降低车体振动幅值，提高列车运行的稳定性。

3）液压位移放大机构在实现GMA系统位移放大的同时输出力减小。仿真结果表明，当位移放大10倍时，GMA系统的输出作动力已经无法满足列车主动悬架振动控制的要求。因此，在设计放大机构时，要从主动悬架整体性能出发，综合考虑各项参数的要求。