消防服多层织物的热湿舒适性
刘林玉, 陈诚毅, 王珍玉, 祝 焕, 金艳苹,2
(1. 浙江理工大学 服装学院, 浙江 杭州 310018; 2. 浙江理工大学 浙江省服装工程技术研究中心, 浙江 杭州 310018)
消防员防护服是保护消防员在火场环境中免受高温伤害的特殊功能性服装。由于消防服通常具有良好的隔热性能,导致消防员在作业过程中产生热应激从而削弱其体力及作战效率[1-3],因此,现代消防服不仅要考虑服装的功能性,还要注重服装的热湿舒适性[4]。目前各国消防服标准对热湿舒适性的评价指标有:热阻、湿阻、总热损失[5],其中湿阻和总热损失是评价消防服热湿舒适性的2个关键指标。织物的湿阻越低,越容易在高温环境中维持人体的热平衡[6]。总热损失是指人体和环境之间总的热量交换。
以往关于消防服织物的研究主要集中在功能性方面,即探究织物的阻燃性能和热防护性能[7-9]。虽已有学者[4,6]对消防服的热湿舒适性进行了一定的研究与评价,但大都采用出汗热平板仪或出汗暖体假人测试织物或服装的热湿阻、总热损失,而这些设备国内普及使用较为困难。本文采用传统的织物隔热、透湿测试方法对消防服多层织物组合的热阻、湿阻和总热损失进行测试和分析,探讨影响消防服织物热湿舒适性能的主要因素,对织物组合的总热损失与其克罗值、透湿率间的关系进行分析,为评价消防服织物的舒适性提供一定的参考。
1 实验部分
1.1 实验材料
本文实验选取目前国内消防服的11种常用面料(市售),包括外层、防水透气层和隔热舒适层。所选试样有芳纶1313、芳纶1414、带PTFE膜的无纺毡覆膜等。各层面料的基本参数见表1。其中:外层面料为A1~A8;防水透气层面料为B1、B2;隔热舒适层为C。模拟消防服的层次构成,由各单层面料组合为3层织物系统,为更加全面地研究织物的不同配伍组合对其热湿舒适性能的影响,利用外层和防水透气层为因子混合水平正交表设计8种组合作为多层织物组合的试样。
1.2 测试方法
1.2.1 织物基本性能测试
织物面密度采用精度为±0.1 g的电子天平进行测定;厚度采用YG(B)141D型数字式织物厚度仪按照GB/T 3820—1997《纺织品和纺织制品厚度的测定》进行测定。根据GA 10—2014《消防员灭火防护服》要求,外层织物阻燃性能按照GB/T 5455—2014《纺织品燃烧性能垂直方向损毁长度、阴燃和续燃时间的测定》进行测定;外层织物断裂强力按照GB/T 3923.1—2013《纺织品 织物拉伸性能 第1部分:断裂强力和断裂伸长率的测定(条样法)》进行测定;织物组合的热防护性能(TPP值)依照NFPA1976—2000《实地消防防护服标准》标准进行测定。

表1 各层面料结构参数Tab.1 Structural parameters of each layer fabrics
1.2.2 织物热湿阻测试
按照GB/T 11048—2008《纺织品 生理舒适性 稳态条件下热阻和湿阻的测定》,采用YG606D型平板式保温仪测试织物的热阻及克罗值。按照GB/T 12704.1—2009《纺织品 织物透湿性试验方法 第1部分:吸湿法》,使用YG(B)216-Ⅱ型透湿量仪测试织物的透湿性能。
其热阻的换算公式如下。
Rct=0.155K
(1)
式中:Rct为试样的热阻,m2·K/W;K为试样的克罗值,clo,clo为热阻的一个表示单位,指在温度为21 ℃、气流不超过0.1 m/s的环境条件下,静坐者(其基础代谢为58 W/m2)感觉舒适时其所穿服装的隔热值为1 clo。
各试样的湿阻换算公式为
(2)
式中:Ret为试样的湿阻,m2·Pa/W;ΔP表示试样两侧的水蒸气压差,Pa;W表示透湿率,g/(m2·h);α表示水的蒸发散热系数,W·h/g。实验在温度为38 ℃,相对湿度为(90±2)%的环境中进行。通过查表计算可知,ΔP=5962.5 Pa,α=0.669 W·h/g。由此再根据式(2)计算出试样的湿阻值。
1.2.3 织物组合的总热损失测试
总热损失是衡量织物热湿舒适性的一个较为客观、全面的指标[13]。按照美国建筑物灭火防护标准 NFPA 1971—2013《建筑火灾及近火作战防护装备标准》要求防护服的总热损失不低于 205 W/m2。根据多层织物的热阻和湿阻,计算织物组合的总热损失。计算公式如下:
(3)
式中,Qt为织物组合的总热损失,W/m2;Rct为试样的热阻,m2·K/W;Ret为试样的湿阻,m2·Pa/W。
2 结果与分析
2.1 织物基本性能测试结果
8种外层织物的阻燃性能、断裂强力以及相应织物组合热防护性能(TPP值)的实验结果见表2。其中织物组合按照外层、防水透气层、隔热舒适层的顺序叠放在一起,模拟消防服的层次结构。结果表明各试样基本性能均达到GA 10—2014消防员灭火防护服标准。

表2 织物基本性能试验结果Tab.2 Test results of basic properties of fabrics
2.2 热阻分析
单层织物的热阻值如表3所示。可以看出,隔热舒适层C的热阻值相对较大,这主要是由于隔热层是无纺布结构,隔热性能好;其次是因为织物的厚度远大于其他面料。因此,尽管面密度小于外层织物,其热阻也最大。控制织物面密度,运用SPSS软件对单层织物的热阻和厚度进行偏相关分析,结果显示织物厚度与热阻的相关系数为0.879,属于显著相关。说明控制织物面密度后,织物越厚,热阻越大。

表3 单层织物的热阻Tab.3 Thermal resistance of single layer fabrics
对多层织物组合的热阻进行测试与换算,并与各组分织物热阻的累加和相比较,其中测试换算值记做实际热阻,加和值记做理论热阻,结果见表4。可以看出,在防水透气层和隔热舒适层不变的情况下,多层织物组合的热阻值相差不大,每个织物组合的实际热阻均低于其理论热阻。其原因是实验仪器测试换算的热阻值是织物与边界空气层热阻之和,而多层织物组合后边界空气层并没有相应增加[10],因此导致实际热阻低于各组分织物的累加和。这说明,空气层厚度会影响织物的热阻值。因此增加织物组合间空气层的厚度,将有助于提升织物系统整体的隔热性能[11]。运用SPSS软件对织物组合的热阻和面密度进行偏相关分析,结果显示织物面密度与热阻的相关系数为0.715,属于中度相关。说明控制织物系统厚度后,织物系统面密度越大,热阻越高,隔热性能越好。
2.3 湿阻分析
单层织物的湿阻值如表5所示。可以看出,防水透气层B1、B2的透湿率满足GA10—2014标准,均大于208 g/(m2·h)。外层织物中A2、A3织物的湿阻明显大于其他织物,这可能是由于在外层织物面密度大致相同时,该织物芳纶1414纱线明显粗于其他织物纱线,纱线越细,织物的毛细高度越大,传递液态水的能力就越强,反之湿传递能力就越差[12]。防水透气层B2的湿阻明显大于B1。与其他层织物相比,隔热舒适层的湿阻相对较低。

表4 多层织物组合的热阻Tab.4 Thermal resistance of multi-layer fabrics

表8 总热损失相关系数Tab.8 Total heat loss of coefficients
注:B为回归系数;sig.表示显著性;t表示显著性检验值。
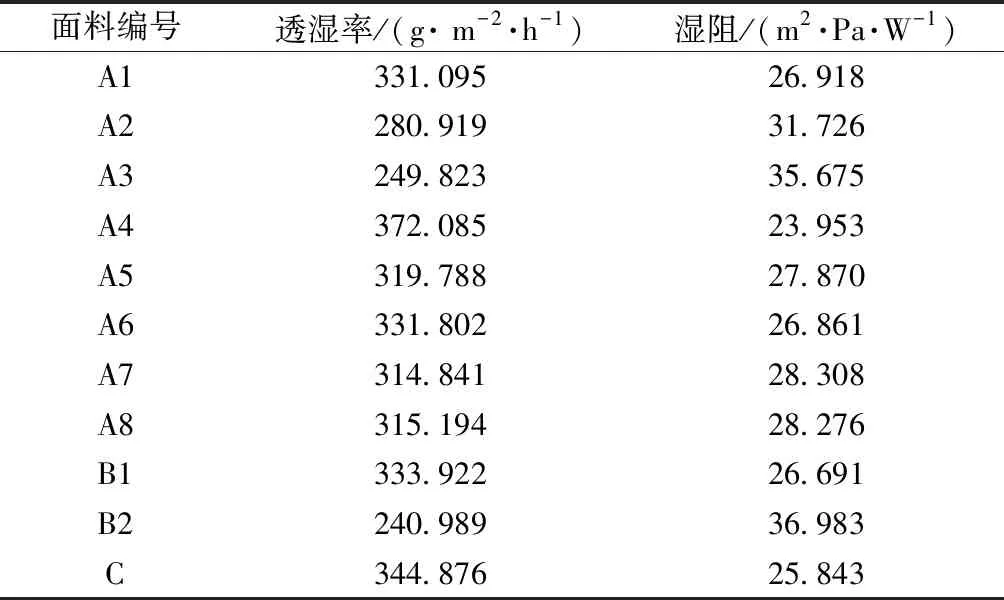
表5 单层织物的湿阻Tab.5 Moisture resistance of single layer fabrics
多层织物的湿阻见表6。可发现,2#、3#织物组合的湿阻仍明显大于其他织物。控制织物厚度,利用SPSS对织物组合的湿阻和面密度进行偏相关分析,相关系数为0.518,具有中度正相关性,表明织物系统面密度越大,湿阻越高。
2.4 织物组合的总热损失分析
总热损失计算结果如表7所示。可以看出,本文选取的几种面料组合虽满足我国的GA 10—2014消防员灭火防护服标准,但在热湿舒适性方面与美国NFPA 1971—2013 标准相比还存在一定的差距。控制织物面密度,运用SPSS软件对织物组合的总热损失和面密度进行偏相关分析,得到相关系数为-0.722,具有中度负相关性。说明织物系统面密度越大,织物的总热损失越小,热湿舒适性能越差。
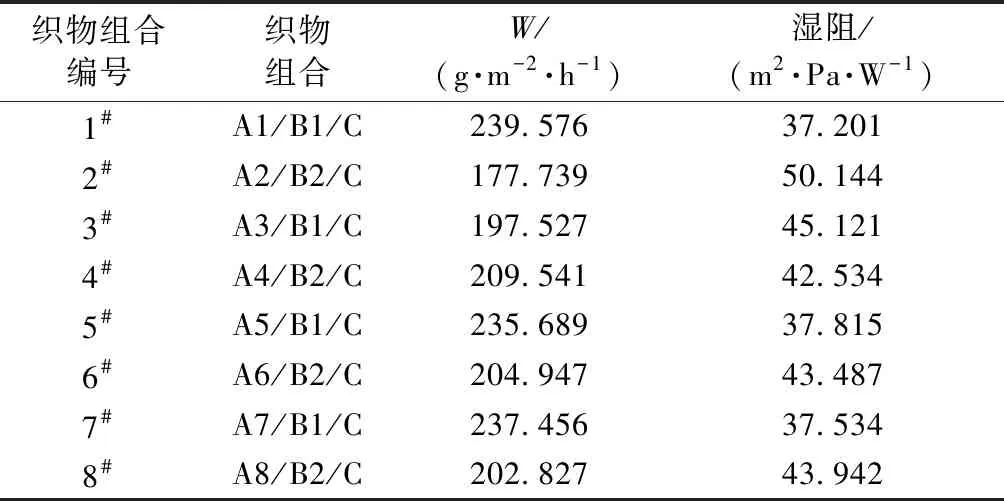
表6 多层织物组合的湿阻Tab.6 Moisture resistance of multi-layer fabrics
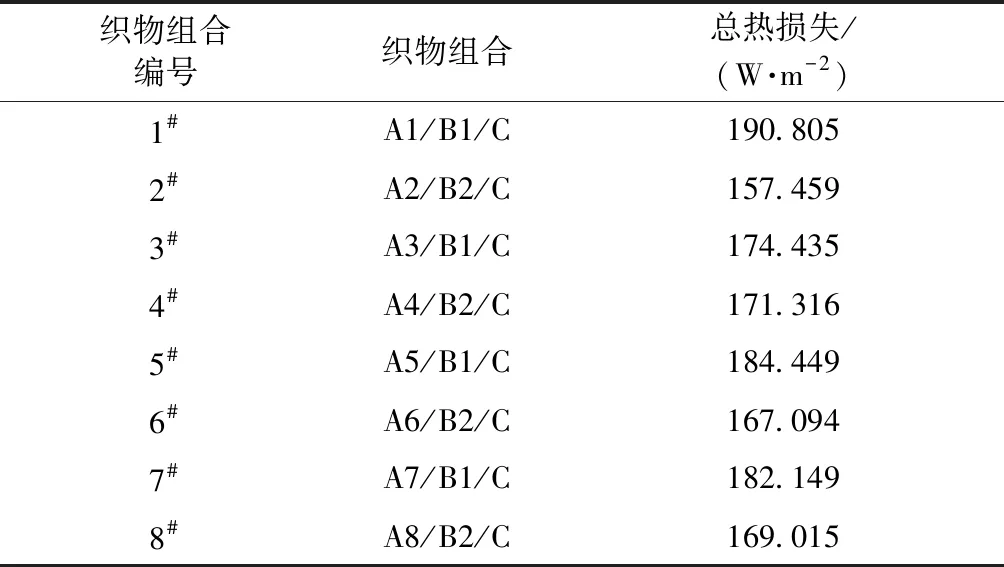
表7 多层织物组合的总热损失Tab.7 Total heat loss of multi-layer fabrics
由于本文实验中织物的热阻和湿阻值并不是通过现有仪器直接测出,同时为解决多个指标多重共线性的问题,避免参数间的相互影响和干扰,故进一步对织物组合的克罗值(K)、 透湿率(W)与因变量总热损失(Qt)之间用多元线性回归方法进行回归模型建立。其回归分析结果如表8所示。
从表8可以得到其多元线性回归方程
Qt=162.9-147.263K+0.342W
(4)
方程中2个指标的容差远大于0.1,方差膨胀因子值远小于10,说明2个指标不存在共线性,可以独立地表示织物组合的总热损失。
3 结 论
1)实验所选用织物的热学性能、力学性能均满足GA 10—2014消防员灭火防护服标准,可用于我国消防服。但所选织物的总热损失与美国标准要求还有一定差距,热湿舒适性方面有待加强。
2)单层织物厚度与热阻值存在显著正相关性;多层织物系统的面密度会对织物系统的热湿阻以及总热损失产生影响,织物系统面密度越大,其热湿阻越高,而总热损失越低,热湿舒适性能越差。
3)空气层的厚度会对织物热阻值产生影响。适当增加织物组合间的空气间隙,将有助于提升织物系统整体的服用性能。
4)通过多元回归分析,织物组合的克罗值(K)和透湿率(W)之间不存在共线性,可以独立表示织物组合的总热损失(Qt),其多元线性回归方程为总热损失Qt=162.9-147.263K+0.342W。
FZXB

