基于供需平衡条件下的城市出租车模型分析

李春平

(山西大学商务学院 数学教学研究部，山西 太原 030031)

0 引言

出租车是城市居民出行的重要交通工具之一，但“打车难”问题也随之而生.随着“互联网+”时代的快速到来，已有多家公司建立起打车软件的服务平台，达到乘客与出租车司机之间的信息互通，同时还推出了各种形式的出租车补贴方案，如文[1-3].在对出租车供求情况的详细了解和全面合理分析的基础上，建立一套实用范围广，可操作性强，消费者满意，司机不跑空趟的方案是势在必行.针对所要解决问题，假设自然条件不好时出租车的平均行进速度为28 km/h；而自然条件较好时出租车的平均行进速度为50 km/h.

1 出租车供需平衡的模型分析

1.1 数据的收集与分析

挑选出我国不同地区的6个城市的出租车情况进行数据收集，并统计成表1.

表1 不同城市出租车的数据统计

表2 不同城市出租车在一天内各个时间点的租车需求量 续表

利用excel计算机软件可以对表1和表2进行了相关分析，得到6个城市出租车的一天内各个时间点的租车需求量数的散点图和拟合曲线图.见图1，2.

图1 不同城市出租车的一天内各个时间点的租车需求量数的散点图图2 不同城市出租车的一天内各个时间点的租车需求量的拟合曲线图

1.2 出租车供给量的模型建立与求解

1.2.1 出租车可供承受的城市居民出行的数量

出租车可供承受的城市居民出行的数量，即指出租车可承受乘客行驶的路程与乘客数量之积，即：

Q=PBRD.

(1)

C=M0+(D-S)M.

(2)

(3)

上式中：Q为出租车承担的居民出行周转量(万人/km)；S为出租车起步里程(km)；P为居民总量(万人);B为居民出行率(次/日)；R表示出租车在人们选择出行方式中可承担的比率(%)；D为居民采用出租车出行的平均出行距离(km)；M0为出租车起步费用(元)；

C为居民单次乘坐出租车的平均花费(元)；m为出租车每公里运营费用(元/km).

1.2.2 出租车每日日总载客行驶里程

出租车在所载客人数量不定的情形下，我们通过计算出租车平均载客数量，来计算客人所行驶的路程.故，出租车全天总载客的行驶路程为：

G=Q/Z.

(4)

式中：G为出租车全日总载客行驶里程(km)；Z为出租车每车平均载客数(人/车).

1.2.3 空驶率的定义

出租车空驶率是指单位时间内出租车空载行驶里程与总行驶里程之比[1].即

(5)

(5)式中：E为出租车空驶率(%)；h为全日出租车平均运营时间(h)；L为全日出租车载客行驶路程；V为出租车平均运营速度(kin/h)；n为城市出租车拥有量.

1.2.4 出租车拥有量的计算

出租车空载率=全天出租车载客行驶路程/全天行驶总路程之和.

并可得知出租车数量的计算方法，即：

(6)

但是由于居民的出行量受时间变化的影响，所以根据各大城市具体的出行特征，需要确定居民使用出租车出行方式所占比例较大的时段.因此，对公(6)修正，得出：

(7)

(7)式中：x/y为出租车在(yT)单位时间内(小时)内承担了为百分之x的出行量.

若要实现一个城市出租车所有量的合理化，需先确定出租车合理的空载率，这个数值的确定通常要考虑城市的规模、人口的数量、道路的规划大小、交通的状况以及居民可支配的收入多少等.

1.3 出租车需求量模型的建立与求解

定义符号：

G：乘坐出租车人口；S：人口平均发展速度；t：时间段；C：出行强度：单位时间内出行总量与人口数的比例.可以乘坐出租车的总人数表示为：

G=Cst.

(8)

通过对我国6个不同城市出租车的一天内各个时间点的出租车需求量数据的收集，以及利用excel软件的分析与拟合，可以预测出租车的需求量.

1.4 不同时空下出租车供需关系的模型分析

1.4.1 模型条件假设

1)在单位时间，某街口处正等待出租车的乘客数量服从于泊松分布：

(9)

2)已乘出租车的每位乘客在不同街口下车的数量也服从于泊松分布；

3)出租车的运行时间只包括乘客上下车时间和必要的运行时间，不考虑其他时间因素.

4)出租车的出勤率保持一致.

1.4.2 出租车的供需均衡模型[4]

1.4.2.1 出租车的空间供需均衡模型[5]

假设L(E、F)中E为交通区域集，F为有向路段集，I和J分别为乘客出发区域集和到达区域集.在出租车的供需相对均衡状态下，载客出租车从i街口(不包括j街口)去j街口，来实现目的地为j街口的出租车需求，同时在j小区出租车变为为空载状态，即

∑i∈IDij=Dj.

(10)

(10)式中：Dij是从i街道到j街道产生的载客需求量；Dj为j街道的空驶出租车数量.

出租车在j街口完成载客后成为空载状态，并在j街口利用软件平台搜索到i街口想要乘坐的客人.在空载状态下，以概率P行向i街口并接到乘客，那么出租车从j街口行向i街道的空载交通量K可表示为：

(11)

假设出租车不在所到小区进行停留，每到达一处后立即进行搜索并离开.那么，出租车在某街道集出行的总量，就是车辆以最短的路程从j街道以空载的情形下到达i街道，并在此街道变为拉客的情况.若从j街道行驶向i街道的空载车辆总和为i街道的出行总量Si，那么

(12)

1.4.2.2 时间供需平衡模型

出租车总营运时间为总载客时间和空载时间之和.

其中，总载客时间:

q0=∑j∈J∑i∈IDijtij.

(13)

总空驶时间：

(14)

因此出租车的总运用时间可表示为：

(15)

若令N为出租车规模，即研究范围内出租车总运营车辆数.

即，在各时间点上出租车关于乘客对其需求量的关系模型为：

(16)

从式(16)可知，在已定的行车路线和出租车需求量固定的条件下，此模型成为对出租车在对应小区搜索顾客的平均时间为ti的关系，且小区数量即为出发的区域数目.

2 建立出租车打车软件服务平台及补贴方案的模型

出租车的供给量随着我国补贴方案的逐渐完善，出租车的数量会逐渐增加.但另一方面，随着我国私家车的逐渐增加又导致了出租车的需求量呈现递减状态.要解决我国“打车难”问题，必须找到出租车供求的平衡点.鉴于以上分析和本文前两问题的研究，提出以下打车的软件服务平台及补贴方案，并进行相关的论证分析.

2.1 新的打车软件服务平台及补出租车的贴方案

2.1.1 新的打车软件服务平台

2.1.1.1 模型前提假设

(H1)假设可出行出租车比率与乘客所等待的时间是反比例关系，即t=k2/p2；其中k2是固定系数.假设顾客的满意度跟等待时间成负相关，且满足s=100-k1*t，其中t为顾客等待打车时间，k1为常系数，顾客的满意度跟的士的覆盖率成正相关.

(H2)假设软件公司为用户提高的生活服务质量日趋完善，出租车司机的覆盖率每年增长，但增长速度每年递减，最后使用打车软件的人数稳定在一定数量(即达到饱和状态).

(H3)假设的士司机因打车软件每月多赚取的收入J为司机因降低空载率而省下的油费，并假设司机每月跑的路程不变，为l，而每公里油费为0，而使用软件前的空载率为w1，使用软件后的空载率为w，w跟p1呈正相关，跟p2呈负相关.软件收取向司机的额外收入提成为p%.

(H4)打车软件开拓的市场基本成熟，大公司的投资也不再，补贴也不再，利用生活服务来增强对用户的粘性.

(H5)打车软件收取的广告费H跟打车软件的覆盖率及使用的频率成正相关，且满足H=k5*v*N(p1+p2)，N为全国总人数.

(H6)假设顾客的覆盖率与满意度成正比.

2.1.1.2 模型构成

2.1.1.2.1 覆盖率的变化规律

出租车司机的覆盖率p2的变化规律

由假设(H1)知，随着时间的推移，固定街道出租车的覆盖比例会逐渐减少，最终呈现接近于一个固定值的状态.这一变化规律符合数学中的指数函数模型，从而假设p2

p2=[k3*e(-n+k4)]+b1.

(17)

其中k3，k4，b1为常系数，n为年份.

顾客的覆盖率p1的变化规律

根据假设(H1)和(H3)，出租车司机的覆盖率与顾客的等待时间成反比，即t=k2/p2；顾客的满意度跟等待时间成负相关，且满足s=100-k1*t，由这两个式子得到

s=100-k1*k2/p2.

(18)

且由假设(H6)顾客覆盖率p1与满意度s成正比，易得

p1=k7*[100-k1*k2/p2].

(19)

2.1.1.2.2 打车软件每年收取的广告费H的变化规律

根据假设(H6)，可得到向用户收取的广告费与用户的覆盖率p1，p2及频率v呈正相关，我们有

(20)

向出租车司机收取的费用E的变化规律.

基于假设(H3)，空载率为w跟p1呈正相关，跟p2呈负相关.

便假定其满足以下等式

w=k8*p1-k9*p2+b2.

(21)

因此易得每月司机省下的油费为(w1-w)*1*o

而每月向出租车司机收取的费用J的变化规律为

J=k6*(w1-w)*1*o.

(22)

而每年向出租车司机收取的费用J的变化规律为

E=12*J.

(23)

打车软件的总利润

Y=H+E.

(24)

2.1.2 新的打车软件服务平台补贴方案

2.1.2.1 模型条件

以下全部补贴满足以下假设条件：

1)乘客对出租车司机评价为满意，并且接单比例达到80%以上，没有中级投诉(即：无理由拒绝载客，客人上车后后又无理由取消或者要求客人自己取消等)；

2)不超过2个初级投诉(高级和优选型司机需衣着整齐，车里备有水，会使用导航等)；

3)无刷单、上车后下单、私自预约客人、私活放置平台下单等行为；

4)关于评星、接单数据以系统记录为准.

2.1.2.2 模型建立

在以上假设条件成立的基础上，为了解决出租车司机与乘客之间信息不对称，导致在高峰期时段、出租车与乘客距离较远等情况下司机随意弃单的问题，我们建立了一个新的对出租车司机进行奖励政策的打车软件服务平台补贴方案，来缓解“打车难”的问题.方案见表3，4.

表3 高峰时段奖励表

其中：早高峰期(周一～周五7:00-10:00)3.5倍车费获得；

晚高峰期(周一～周四17:00-23:00；周五/六18:00-24:00)2.5倍；

周日全天，2.5倍车费获得；其他时段，均2倍车费获得；

每趟奖励最高为50元.若同时获得多项奖励可以采取以下合并奖励制度：

表4 奖励金额关于单数的数据表

2.2 出租车车数预估模型的建立

首先假定：城市面积并没有较大的改变；人口的消费能力没有较大的变化.

其次，设定变量：记相关影响常数是c1，第i年乘坐出租车人数为xi.

城市路况：路况因素又分为自然(雨雪气候)因素和人为(道路拥挤)因素.记其影响系数为c2，ui为城市路况；

在天气情况或路面交通条件较差时出租车行驶的平均速度v1=28 km/h；条件较好时出租车行驶的平均速度v′1为50 km/h.

记第i年出租车的拥有数量是Pi(i分别为2010，2011，2012，2013)，并有，Pi(i=2010)=10 018，Pi(i=2011)=11 433，Pi(i=2012)=12 115，Pi(i=2013)=12 929，Pi′=c1xi+c2ui

将以上数据代入下面的公式

(25)

Pi′=c1xi+c2ui

(26)

利用lingo软件可以求得其影响常数值c1=0.19，c2=0.167 3.

结论：通过上式可以根据过去几年出租车的数量预估出未来的出租车数量.

2.3 出租车定价的预测模型

参考我国对出租车起步定价的政策，制作我国某城市从2008年到2015年出租车的起步定价表，如表5所示.

表5 过去8年的某城市的出租车定价变化

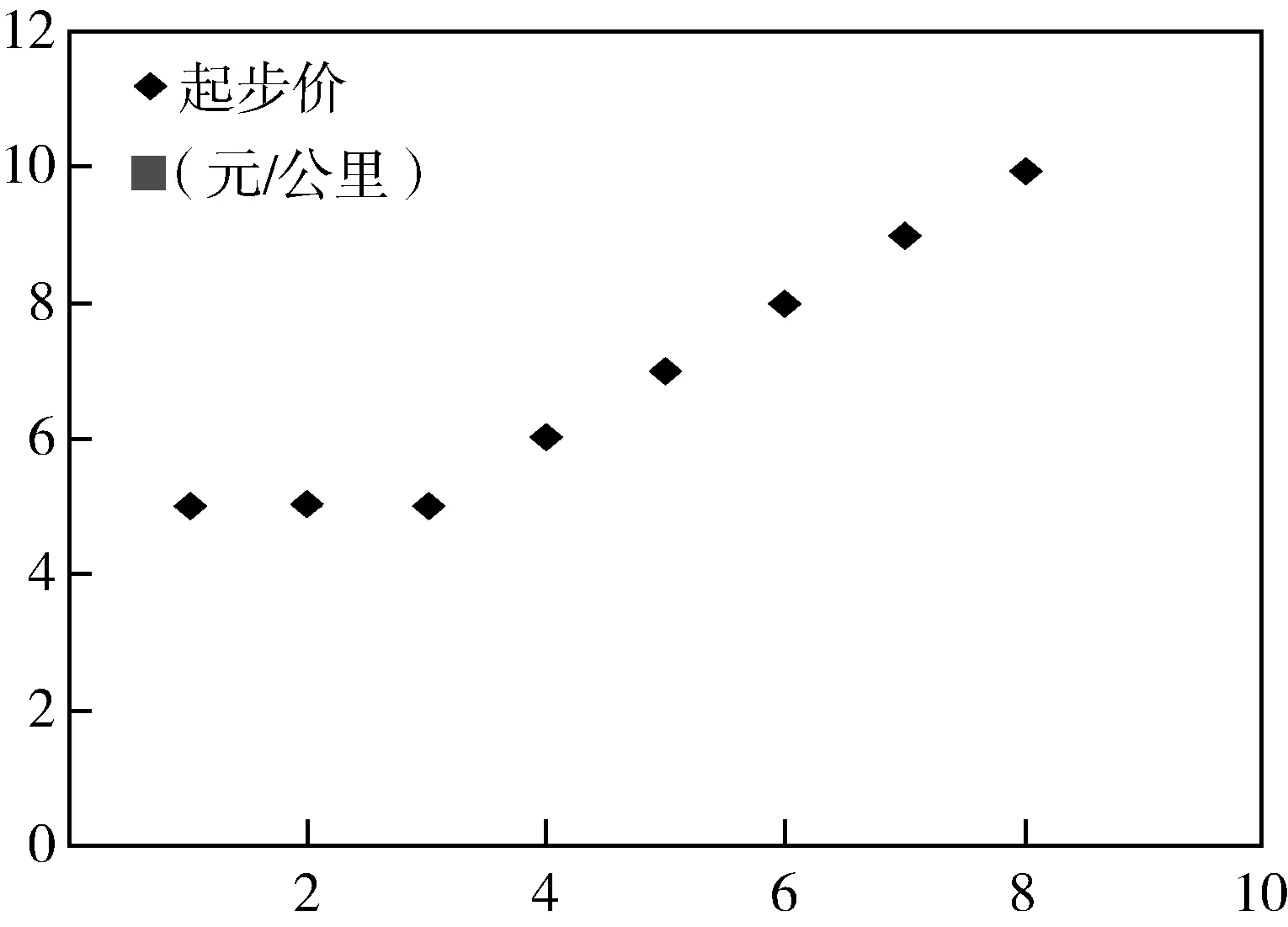
图3 8年某城市出租车定价散点图

利用Excel软件对表5进行数据分析，得到城市出租车起步价随着时间变化的散点图，如图3所示.

运用过去的多个按照时间次序排起来的相同变量的观测数值(其中，时间次序数作为权数，利用得到的观测值求其加权算术平均数)来预测以后此变量数值的变化趋势.即：

(27)

将上述8年的出租车定价变化代入加权平均数公式可求出最适宜的起步价.

结论：

最适宜的平均起租价为8.0元,最适宜每公里定价： 2.5公里/元.

2.4 出租车最大利润的模型建立及计算

2.4.1 模型建立的条件及定义

首先，本模型的建立需要假设总行程路线为X，空载行程数X2，是定数，其次引用空载率的定义：单位时间内出租车空载行驶里程与总行驶里程之比.

(28)

其中：E为出租车空驶率(%)；h为全日出租车平均运营时间(T)；L为全日出租车行驶全里程(km)；v为出租车平均运营速度(kin/T)；n为城市出租车拥有量.

2.4.2 出租车最大利润的模型建立及计算

通过统筹学的非线性规划可以得到司机满载时所得净利润模型：

W1=8+2.5(X-X2)+(-CX2).

(29)

(29)式中：W为司机满载时所得的净利润；C为每公里耗油量.

将C=0.8(耗油量/km)代入(29)式

司机空载时所消耗的费用

W2=CX2.

(30)

(30)式中：W2为空载时所消耗的费用；X2为空载时行驶的距离.

(31)

司机可获得的最大利润：

maxW=W1+W2.

(32)

将(28)(29)(30)(31)代入(32)，并将T=8，n=12 115代入，得到司机可获得的最大利润为：

(31)

根据(31)式可以求出司机可获得的最大利润.

2.5 模型评价

优点：所建立模型能接近实际，针对问题进行建模并求解，使得此模型具有较好的实用性和推广性；模型在计算过程中采用了专业的数学软件，准确率较高；文中数据真实，并通过excel软件分析，找到了变量间相互的潜在关系；对模型中所涉及到的影响元素进行量化分析，使得结论更具说服力.

缺点：模型的约束条件相对简单；乘客对出租车满意度调查的理论依据较为匮乏.