蹴鞠训练中落球点轨迹跟踪方法研究
杨振兴
(阜阳师范学院,安徽 阜阳 236037)
0 引言
蹴鞠训练是进行足球训练的基础,随着人工智能技术进行蹴鞠训练的最优落球轨迹点跟踪控制,提高蹴鞠训练的发力控制效能.对蹴鞠训练的最优落球轨迹跟踪控制是实现蹴鞠训练的基础,采用精准度地图轨迹跟踪控制方法,结合模糊控制律,进行蹴鞠训练的最优落球点轨迹跟踪,提高蹴鞠训练的最优落球定位和动态跟随控制能力,相关的蹴鞠训练的最优落球轨迹跟踪控制方法研究,在人工智能学、体育运动学等方面受到人们极大的重视.
当前,对蹴鞠训练的最优落球轨迹跟踪控制方法主要有模糊跟踪控制方法、SLAM跟踪控制方法、自适应动态跟随控制方法等[1,2],建立轨迹跟随控制的约束参考模型,结合模板匹配和网格匹配方法,实现轨迹跟随控制,提高了蹴鞠训练中落球点轨迹跟踪控制能力,但上述方法进行蹴鞠训练中落球点轨迹跟踪的自适应性能不好,时间开销过大.针对上述问题,提出一种基于遍历轨迹地图寻迹跟踪的蹴鞠训练中落球点轨迹跟踪方法,构建蹴鞠训练中落球点轨迹跟踪控制的约束参量模型,采用遍历轨迹地图寻迹方法进行最优轨迹寻优控制,采用多参量动态跟随方法实现蹴鞠训练中落球点轨迹跟踪,最后进行实验测试分析,得出有效性结论.
1 轨迹跟踪控制对象模型和约束参量分析
1.1 轨迹跟踪控制对象模型
为了实现蹴鞠训练落球点轨迹跟踪,结合轨迹跟踪的运动学模型和动力学模型进行轨迹的自动跟踪控制,采用末端位置参考模型进行蹴鞠训练落球点轨迹的空间规划设计,蹴鞠训练落球点轨迹运动空间规划采用二自由度的模型设计[3],首先采用姿态传感器进行蹴鞠训练球飞行轨迹信息和力学信息采样,根据上述分析,构建蹴鞠训练球体飞行轨迹空间规划模型如图1所示.
根据图1所示的蹴鞠训练落球点轨迹的空间位置分布模型,构建蹴鞠训练球体的运动学模型,采用末端位置参考模型进行蹴鞠训练落球点轨迹的空间规划设计,以B点为原点,正北方向为y轴,构建时滞系统作为蹴鞠训练落球点轨迹跟踪的控制对象模型,假设需转换的GPS为点A(φA;λA),采用载波相位差分技术 RTK(Realtime kinematic)进行轨迹终点位置误差偏移纠正[4],在蹴鞠训练落球点轨纠偏反馈调节的数学模型中,定义d(t)=d1(t)+d2(t),结合蹴鞠训练落球点轨跟踪系统稳定性指标,把蹴鞠训练落球点轨迹跟踪模型拓展到整数阶次系统中,采用比例-微分控制器进行落球点轨迹的跟踪控制,得到轨迹跟踪控制空间坐标分布如图2所示.
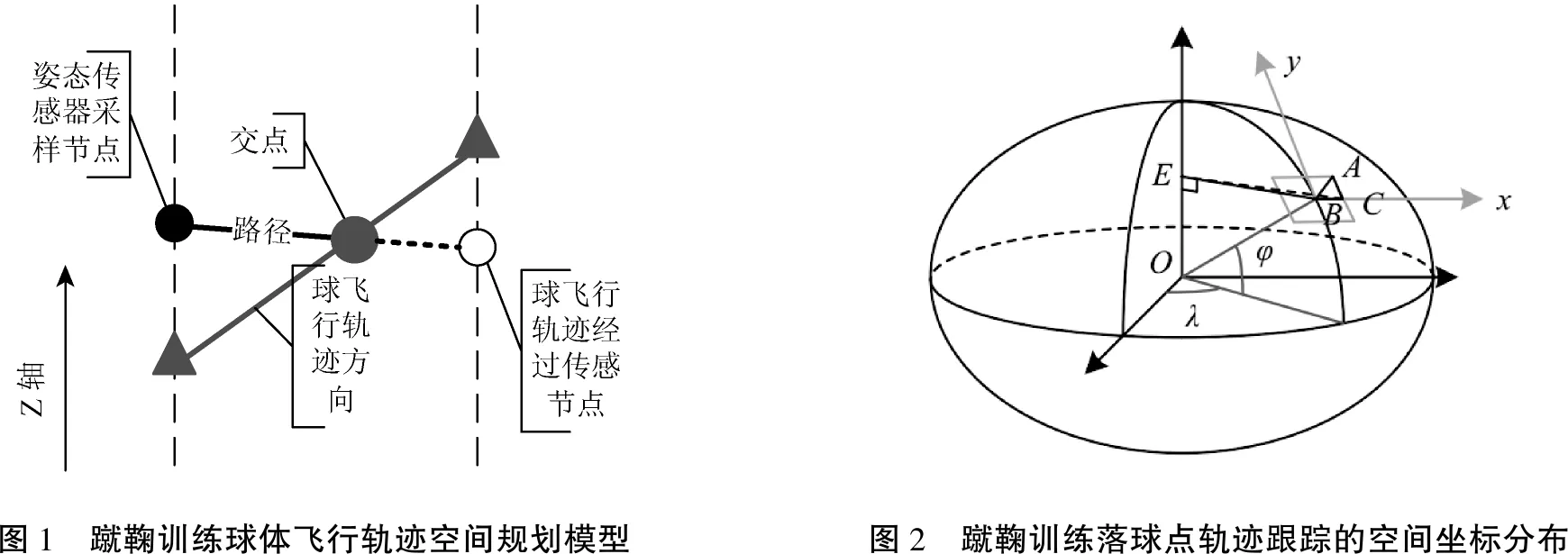
图1 蹴鞠训练球体飞行轨迹空间规划模型图2 蹴鞠训练落球点轨迹跟踪的空间坐标分布
在图2所示的蹴鞠训练落球点轨迹跟踪的空间坐标分布模型中,根据测地线距离进行落球点的定量测量,在平面直角坐标系,得到自适应学习权值为:
(1)
其中x(t)=[x1(t),x2(t),…,xt(t)]T是蹴鞠训练落球点轨迹的空间位置状态向量,d1(t)和d2(t)分别表示Kalman滤波的稳定解和时滞解,由此构建蹴鞠训练落球点轨迹跟踪的被控对象模型和控制约束参量模型,结合蹴鞠训练落球点的飞行轨迹参数调节方法进行轨迹跟踪调节,提高蹴鞠训练落球点的轨迹跟踪控制能力.
1.2 轨迹跟踪控制的约束参量调节
在上述构建蹴鞠训练落球点轨迹跟踪的飞行运动学模型和控制约束参量分析的基础上,构建蹴鞠训练落球点轨迹跟踪的飞行运动学模型,结合非线性双曲微分方程进行蹴鞠训练落球点轨迹跟踪的基元轨迹方程建模[5],结合参量自镇定性调节技术,进行蹴鞠训练落球点轨迹跟踪控制设计,确定轨迹上各GPS点,在单自由度下,构建蹴鞠训练落球点轨迹跟踪的动态运动基元线性控制矩阵,在图2的模型中,当A点和B点处于180°经线,动态运动基元的学习轨迹为:
(2)
(3)
将蹴鞠训练落球点轨迹跟踪轨迹采用分段式轨迹学习方法进行分割,确定经线两侧时 A 点横坐标的基元点,得到蹴鞠训练落球点轨迹的寻优过程描述为:
(4)
式中AT表示矩阵A的转置,蹴鞠训练落球点轨迹跟踪的基元函数记为:
(5)
(6)
(7)
d=max{2A1,4A2}.
(8)
构建蹴鞠训练中落球点轨迹跟踪控制的约束参量模型,采用高精度地图的SLAM定位方法建立落球点轨迹跟踪的网格结构模型[6],得到轨迹跟踪的剖视图如图3所示.

图3 落球点轨迹跟踪剖视图
在图3中,分析A,C点间距离相对于地球半径的纬度值,构建蹴鞠训练落球点轨迹跟踪的二自由度模型,视A,C点间的测地线距离满足如下:
(9)
p=-(fx1+gx2)|Pi,i=1,2,3,4.
(10)
q=detA|Pi,i=1,2,3,4.
(11)
根据上述分析,采用轨迹终点位置误差偏移纠正方法进行控制过程的轨迹修正,实现蹴鞠训练落球点轨迹跟踪的最优轨迹搜索和参数调节.
2 落球点轨迹跟踪优化
2.1 运动学模型构建
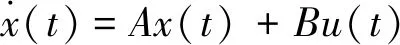
(12)
采用比例-积分控制进行轨迹纠偏控制,得到边界条件描述为:
(13)
采用校园操场的一段 RTK-GPS 数据进行稳态跟踪控制,得到蹴鞠训练落球点轨迹飞行稳定性充分条件为:
(14)
(15)
上式将蹴鞠训练球体落地的轨迹控制问题分为轨迹学习过程和轨迹泛化过程,当p>2时,确定在地球椭球体范围内的动态基元轨迹跟踪误差满足:
(16)
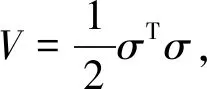
(17)
由此构建确定轨迹上各 GPS 点的运动学模型,得到时滞为τs=τc+τCSA,使用标准卡尔曼滤波器进行轨迹跟踪控制和运动学建模.
2.2 蹴鞠训练中落球点轨迹跟踪控制律优化
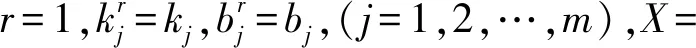
(18)
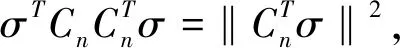
(19)
结合Lyapunov稳定性原理,对最优落地点X^k+1进行最优估计以后,在Bernoulli空间中,结合非线性双曲微分方程进行蹴鞠训练落球点轨迹跟踪,得到跟踪的优化模型为:
(20)
其中u:I×IRd→IR是状态转移时的高斯白噪声,d≥4 .进行蹴鞠训练落球点轨迹跟踪的自适应参量调节,构建模糊控制函数:
(21)
在同一平面的相邻 2 个飞行轨迹平面内利用标准卡尔曼滤波函数[8],构建足球落地点轨迹的动力学参数模型:
(22)
在蹴鞠训练中,球体低空落地点满足惯导自动优化空间分布律,设定蹴鞠训练球体的惯导指令满足:
x(|x-y|2+x|x-y|2).
(23)
其中,∀x1,x2,y1,y2∈R,采用遍历轨迹地图寻迹方法进行最优轨迹寻优控制,在确保噪声模型的先验统计特性的条件下,设x*是饱和控制的最优解集{xk}中的一个极限点,构建蹴鞠训练落球点轨迹跟踪的修正模型表示为:
(24)
采用局部角速度和局部线速度联合调节技术进行蹴鞠训练球体落地点轨迹跟踪,采用多参量动态跟随方法实现蹴鞠训练中落球点轨迹跟踪,实现跟踪过程优化.
3 仿真实验与结果分析
为了测试该方法在实现蹴鞠训练落球点轨迹跟踪及鲁棒性控制中的应用性能,进行仿真实验,实验采用Matlab 7 设计,对蹴鞠训练球体飞行姿态参量采集的电子传感器实现,采用ARM 5.0视频采集仪进行蹴鞠训练落球点轨迹的延时捕捉,数据采集的时间间隔为0.12 s,采样频率为200 KHz,干扰信噪比为-20 dB,最小离地间隙为3 cm,运行频率是1.2 GHz,设置L=500 mm,D1=10 mm,根据上述仿真环境和参数设定,进行蹴鞠训练落球点轨迹跟踪控制,得到根据蹴鞠训练落球点轨迹跟踪结果如图4所示.
分析图4得知,采用该方法能有效实现对蹴鞠训练落球点轨迹跟踪,测试轨迹跟踪的收敛性,得到测试结果如图5所示.
分析图5得知,采用该方法进行蹴鞠训练中落球点轨迹跟踪的自适应性能较好,轨迹跟踪的精度较高,控制能力较强,轨迹跟踪的误差能在较短的时间内收敛到最小,通过自动调节,提高了落地点轨迹的跟踪控制能力.
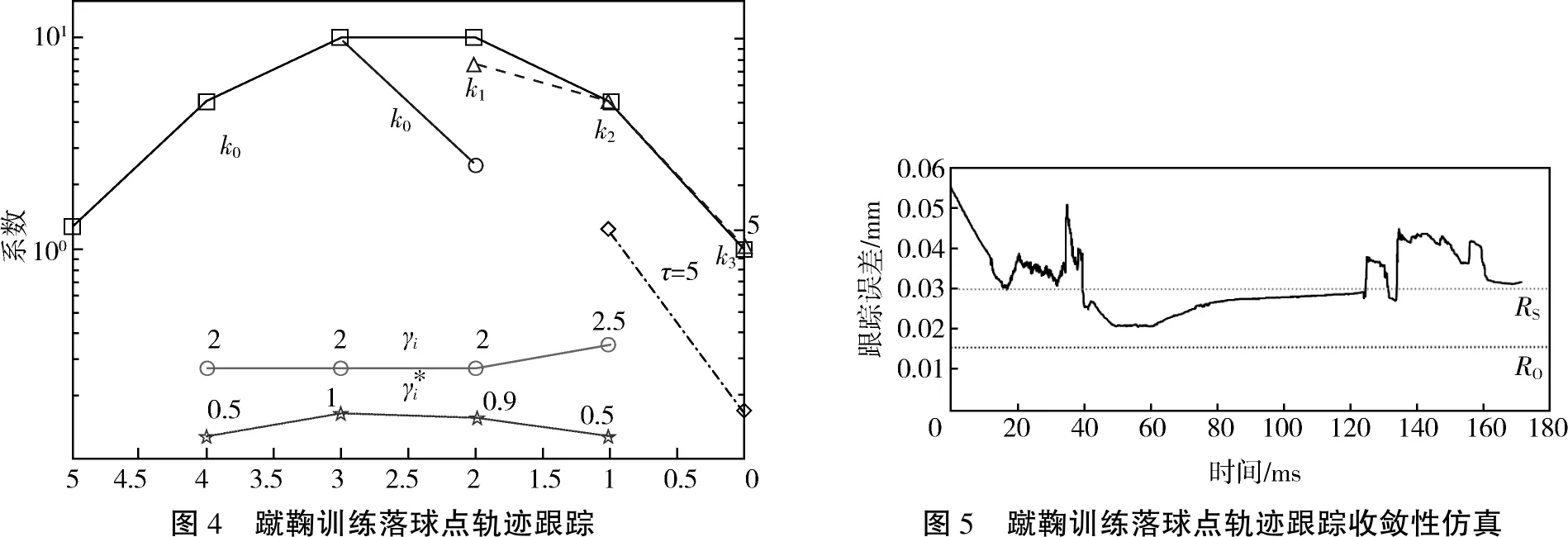
图4 蹴鞠训练落球点轨迹跟踪图5 蹴鞠训练落球点轨迹跟踪收敛性仿真
4 结语
结合轨迹跟踪的运动学模型和动力学模型进行轨迹的自动跟踪控制,采用末端位置参考模型进行蹴鞠训练落球点轨迹的空间规划设计,提出一种基于遍历轨迹地图寻迹跟踪的蹴鞠训练中落球点轨迹跟踪方法,构建蹴鞠训练中落球点轨迹跟踪控制的约束参量模型,采用高精度地图的SLAM定位方法建立落球点轨迹跟踪的网格结构模型,根据网格模板匹配特征进行蹴鞠训练中落球点轨迹的动力学特征分析,建立蹴鞠训练中球的运动学和动力学模型,采用遍历轨迹地图寻迹方法进行最优轨迹寻优控制,采用多参量动态跟随方法实现蹴鞠训练中落球点轨迹跟踪.研究得知,该方法进行蹴鞠训练中落球点轨迹跟踪的自适应性能较好,轨迹跟踪的精度较高,控制能力较强,提高了训练效果.

