矩阵特征值的估计

程克玲

（吕梁学院汾阳师范分校，山西汾阳032200）

作为矩阵的重要参数，特征值可以看做是复平面上的一个点[1]，矩阵特征值的计算与估计在理论和实际应用中都是非常重要的。随着矩阵阶数的增加，特征值的精确计算难度加大，甚至无法实现。

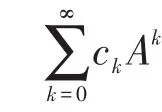
SScchhuurr引理[6]任意n×n实矩阵A，存在酉矩阵U与上三角矩阵R，使得

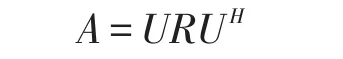
式中，UH表示将矩阵U共轭转置，R中的元素，可能为复数。

证 给定n×n实矩阵A，可以求出A的n个特征值，不妨设为λ1,λ2,…,λn（顺序没有要求）。假设存在上述的U与R，只要将它们求出，即可说明其存在性，同时也说明了其构造或求解的过程。同时为了过程简略，设特征值互不相同。特殊情况再加以说明。

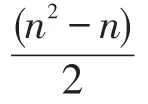
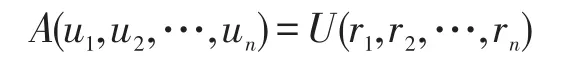
先看乘积的第一列：Au1=Ur1。由于R为上三角阵，且对角元为A的特征值，所以列向量r1只有第一个元素为λ1，其余元素全为0。所以上式就可以化为Au1=λ1u1。u1为A的特征值λ1对应的特征向量当然存在。再利用酉矩阵的性质（不同的列向量都正交，且为单位向量），所以要将u1单位化。这样，得到U的第一列u1。

继续考察Au2=Ur2。

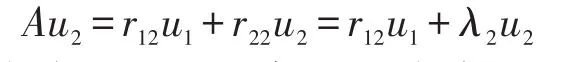
式中含有u2及r12共n+1个变量，需要n+1个独立方程才可解出。然而上式含有n个方程，u1与u2垂直，u2单位长度，共n+2个条件。但在上式中，λ2为A的特征值，所以n个方程并不是相互独立的。列出n+2个方程，刚好可以解出u2与r12。

一般情况，考察Auk=Urk。

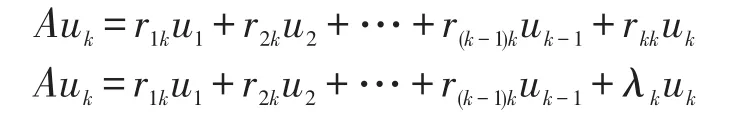
与前面讨论类似，共有uk中的n个变量和rk中的 (k-1)个变量 (r1k,r2k,…,r(k-1)k)，rkk=λk为已知的特征值。所以共有(n+k-1)变量。上式中含有n个方程，利用u1,u2…,uk-1与uk垂直，可得(k-1)个方程，再加上uk为单位向量，共(n+k)个方程，正好可以解出所有的(n+k-1)变量。

如此继续，直到第n步的Aun=Urn。这样，便可以解出所有的rij与uk，矩阵U与R便可以确定了。

定理 11 设A∈Cn×n,λ1,λ2,…,λn是A的特征值，则

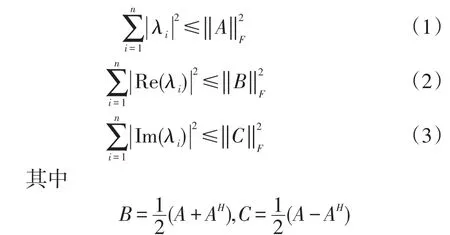
式（1）～（3）中任一等式成立，必有其余两个等式成立。而任一等式成立的充分必要条件是A为正规矩阵。

证 根据Schur引理，对任意的A∈Cn×n,存在U∈Un×n,使A=UTUH，T的主对角线上的元素是A的特征值。由于矩阵的F-范数在酉变换下不变，因此 ‖A‖F=‖T‖F,令T=(trs)(r,s=1,2,…,n,r＞s时，trs=0)，则有

由推论1易得下面两个结论：

1）Hermite矩阵的特征值都是实数；

2）反Hermite矩阵的特征值为零或纯虚数。

因为当AH=A时，C=0,Im(λi)=0,即λi为实数，i=1,2,…,n;当AH=-A时，B=0,Re(λi)=0,即λi为零或纯虚数，i=1,2,…,n.

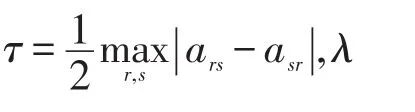
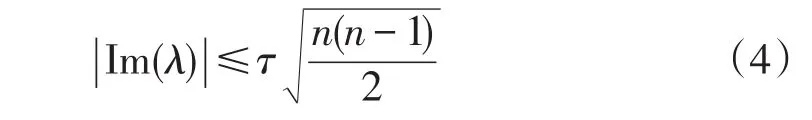
证 由式（3）得

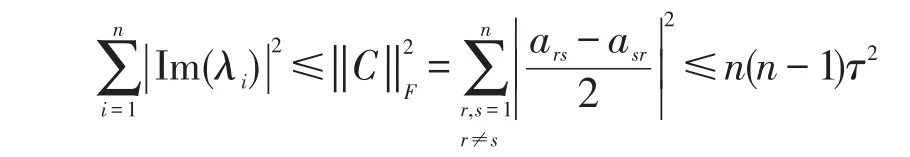
由于A是实矩阵，其复特征值成共轭对出现。因此，当λ是实特征值时，式（4）是自然成立的；而当λ是复特征值时，有

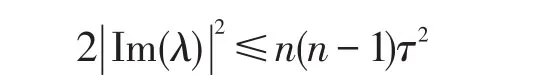
此即式（4）成立。

解A为反对称矩阵，其特征值为

因此，所给矩阵A（实反对称矩阵）的特征值的模不超过0.3464，且由推论2得到的更好些。