新型离心膨胀动态补偿高速刀柄的动力学分析∗∗

王 军 翟玉平 余业龙 张 淳

(燕山大学机械工程学院，河北秦皇岛066004)

随着高速加工技术的快速发展，以HSK为代表的高速刀柄得到了广泛应用，但HSK刀柄的极限转速仍偏低，即在高速下因离心膨胀间隙使刀柄在主轴锥孔内的定位夹紧失效[1-2］。

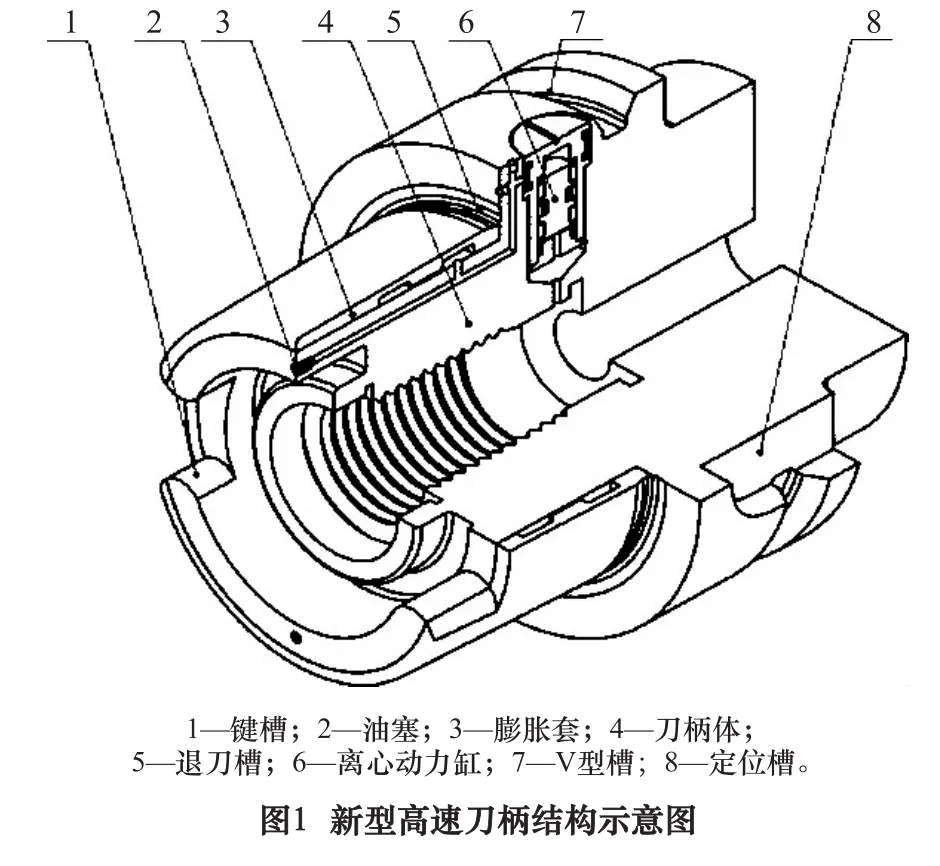
针对这一离心膨胀问题，设计了一种能对刀柄/主轴接口锥面离心膨胀间隙进行动态补偿的新型高速刀柄(发明专利201310197456.7)，如图1所示。

机床夹紧机构通过拉钉拉紧刀柄。当刀柄旋转时，离心动力缸内的活塞在离心力作用下径向移动并挤压液压油，油压升高使膨胀套油腔薄壁产生弹性膨胀，且转速越高变形量越大，补偿接口锥面的离心膨胀间隙，保证刀柄在主轴锥孔内的定位。相比HSKA63，新型刀柄的极限转速更高，达到了 35 000 r/min[3］。本文对其动态性能进行分析。

1 刀柄的模态分析

1.1 新型刀柄的液固耦合模态

动态补偿系统的液压油会增加阻尼，对刀柄动态性能产生影响，故利用Ansys Workbench进行单向液固耦合模态分析，包括三步:液压油流场分析、刀柄体静态结构分析、液固耦合模态提取[4-6］。

(1)液压油流场分析

将在Pro/E中生成的新型刀柄(含液压油)三维实体模型导入Ansys Workbench中重生。在液压油流场分析模块中将刀柄体抑制(suppress body)，只保留油腔内的液压油并利用CFD求解器进行自动划分网格。为提高液固耦合计算精度，网格划分可调用ANSYS ICEM模块。所得液压油的有限元模型如图2所示。

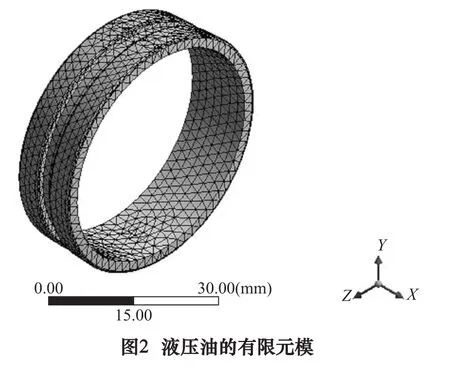
在材料库中添加材料属性:刀柄材料密度7 850 kg/m3、弹性模量206 GPa、泊松比0.3。液压油密度886 kg/m3，声速 1 487 m/s，运动粘度 780 mm2/s。 将液压油假定为不旋转、不可压缩和小幅运动[5］。计算油腔内液压油在0.8 MPa的初始油压P0下的压力场分布，用于后续分析。

(2)刀柄体静态结构分析

在静态结构分析模块(static structural)以六面体单元(hex dominant)进行刀柄体网格划分，建立刀柄体的有限元模型，如图3所示。

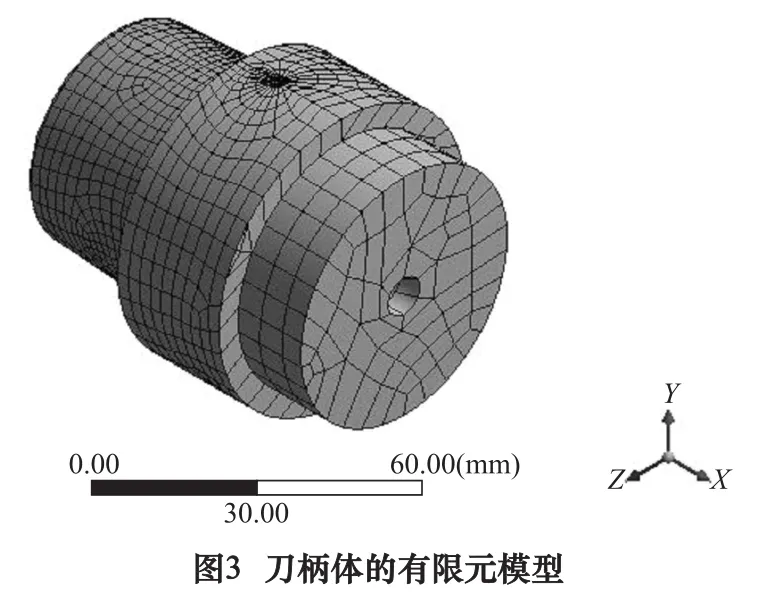
将液压油的压力场数据传输到刀柄锥体上，完成液固耦合(liquid-solid coupling)过程[7］。刀柄体视为线弹性体；将主轴对刀柄的支承作用简化为对刀柄锥面和端面的弹性支承，根据主轴前后轴承刚度估算主轴的径向和轴向刚度分别为190 N/mm3、150 N/mm3；活塞与动力缸(将缸体与刀柄体简化为一体结构)接触柱面为有润滑条件下的无摩擦接触；连接刀柄体与活塞的弹簧刚度k为6.77 N/mm，作用在活塞端面的初始油压P0为0.8 MPa。边界条件施加如图4所示。

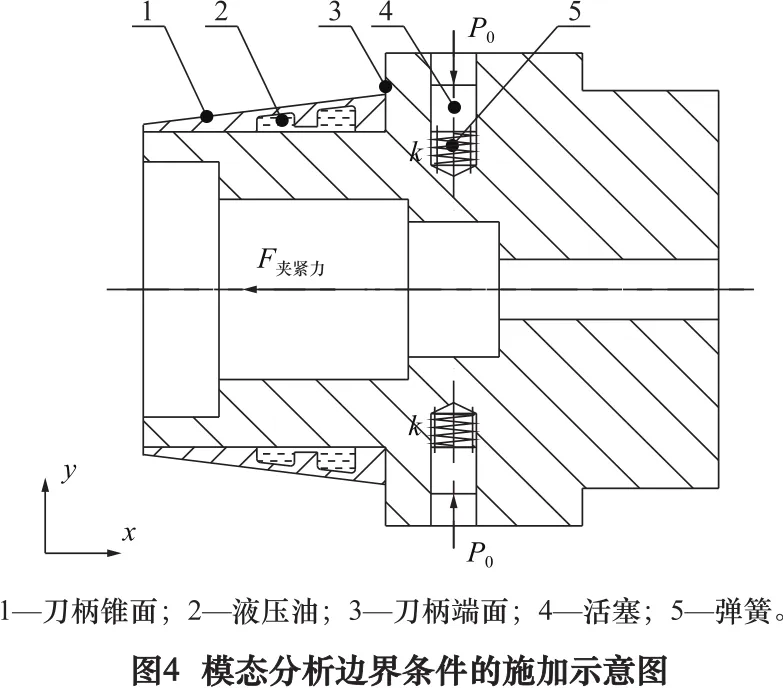
(3)提取液固耦合模态

提取刀柄振动响应的前六阶固有频率和模态振型。如图5和表1所示。

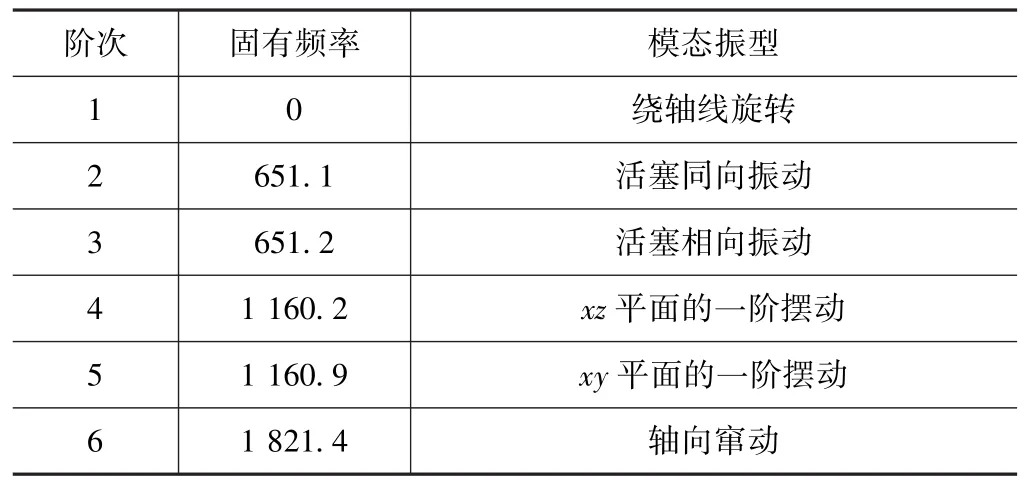
表1 刀柄的前六阶固有频率 Hz

由图表可见:①第二阶和第三阶、第四阶和第五阶固有频率近似相等，说明它们是系统运动微分方程的两对重根，所对应的模态振型是正交的。②最低固有频率为0，是因为数值分析中忽略了支承轴承摩擦、主轴系统不平衡质量等外界因素，刀柄可随主轴系统自由旋转。③系统的最低非零固有频率为651.1 Hz，而新型刀柄极限转速35 000 r/min所对应的转动频率为583.3 Hz，前者大于后者；说明在刀柄极限转速范围内不会引发系统共振。

1.2 与HSK-A63的模态对比

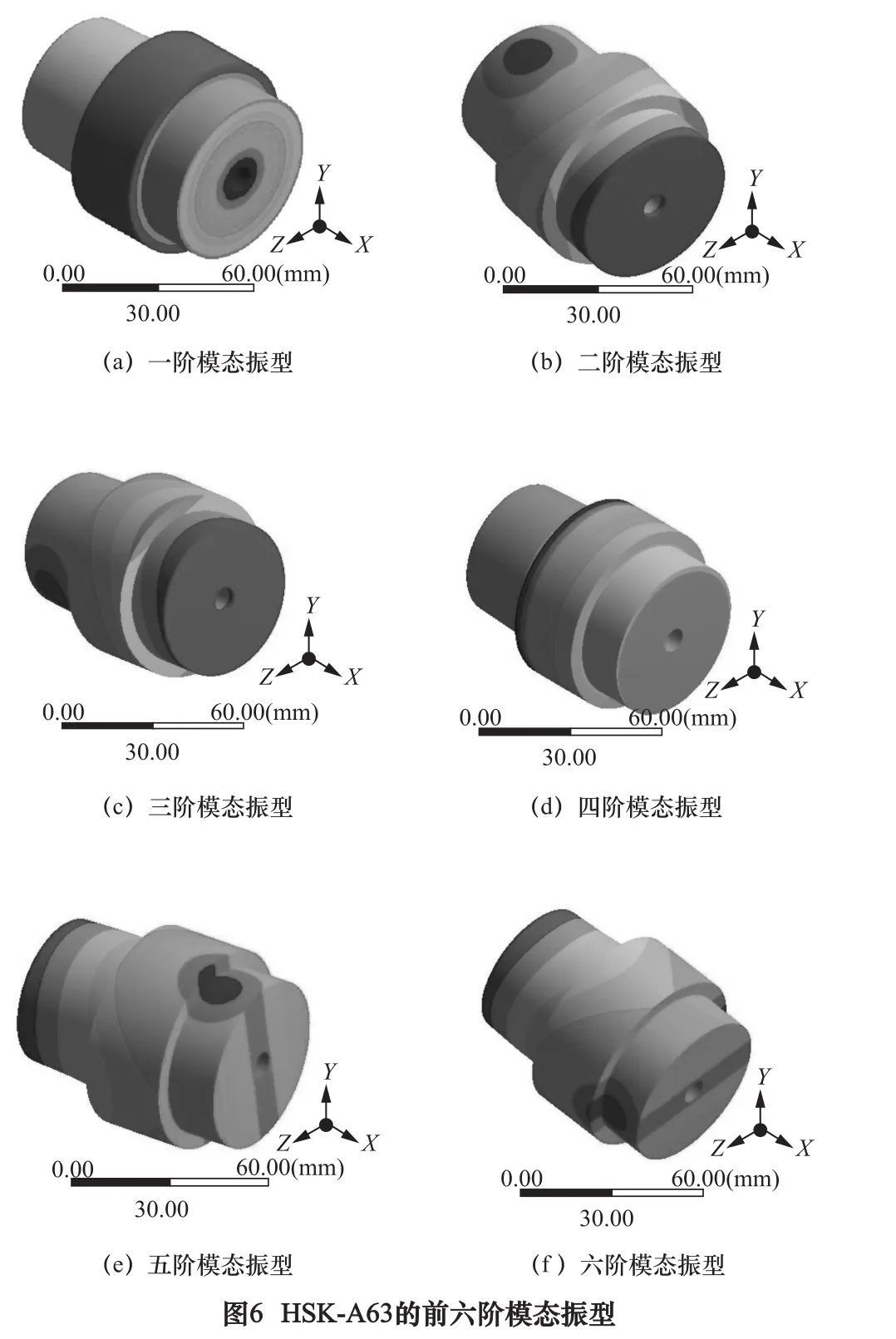
对HSK-A63进行模态分析，有限元建模步骤同新型刀柄(略)。计算提取HSK-A63的前六阶固有频率和模态振型，结果如图6和表2所示。

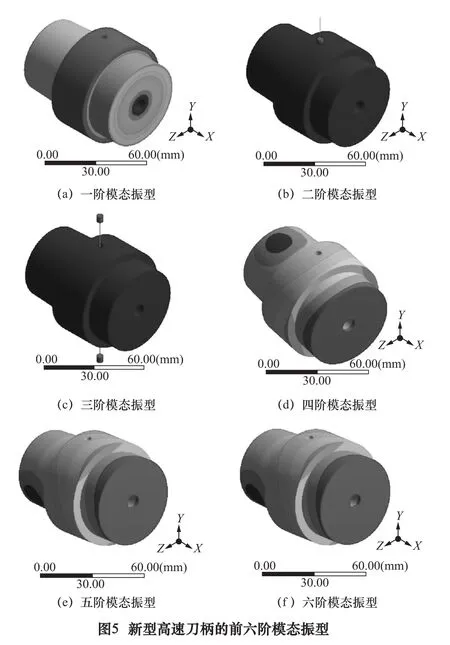
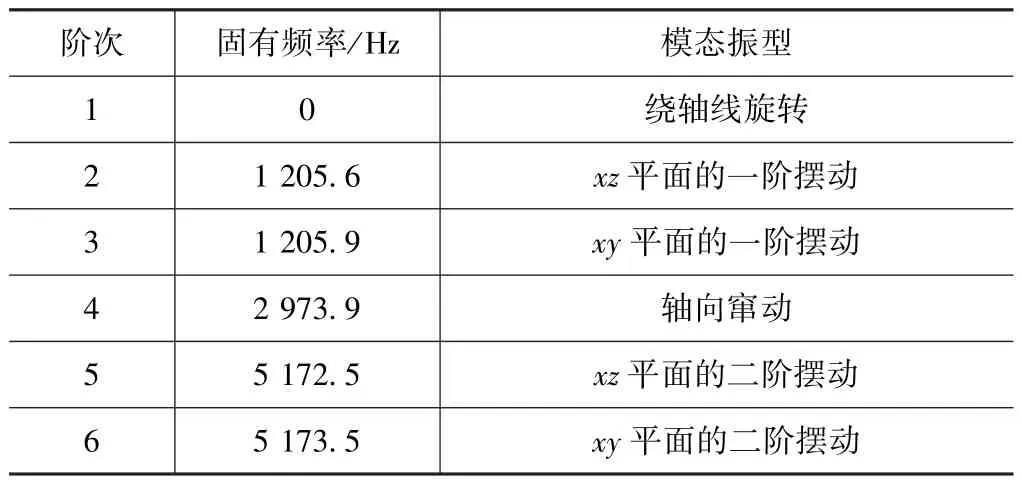
表2 HSK-A63的前六阶固有频率 Hz

对比两种刀柄可见:①HSK-A63的第二阶和第三阶、第五阶和第六阶固有频率很接近，为系统运动微分方程的两对重根，所对应的模态振型是正交的[8］。②新型高速刀柄的第二、三阶模态属于活塞振子(活塞-弹簧)的振动响应且频率较低，是HSK-A63所没有的；第一、四、五、六阶模态分别对应着HSK-A63的前四阶，且新型刀柄的固有频率稍低，这是由于支承刚度相同而新型高速刀柄质量增加(实心锥柄相对于空心锥柄)的缘故。

2 刀柄的谐响应分析

谐响应分析用于确定高速刀柄在简谐载荷(如铣削力)作用下的稳态响应，反映其抗振性。

2.1 新型刀柄的谐响应分析

(1)确定简谐载荷

以幅值100 N、相位角0的简谐载荷F(t)作为激振力；将F(t)作用在刀柄右端横截面，令简谐载荷与活塞振子的振动方向相平行[9］。谐响应分析的其余边界条件同模态分析。见图4(图中未标示F(t))。

由新型刀柄的模态分析知:要得到F(t)作用下活塞振子和刀柄体共振时的谐响应，F(t)的频率f要涵盖二者的固有频率651 Hz和1 160 Hz，故设定激励F(t)的扫描频率为0～1 500 Hz。

(2)求解谐响应

将模态分析数据传输到谐响应分析中，加载简谐载荷；设定求解步数为300(间隔5 Hz)；利用Ansys Workbench的谐响应分析模块，按模态叠加法求解[10］；以活塞上端面和简谐载荷作用点作为提取点。包含活塞和刀柄体固有频率651 Hz、1 160 Hz的幅频响应曲线如图7、图8所示。

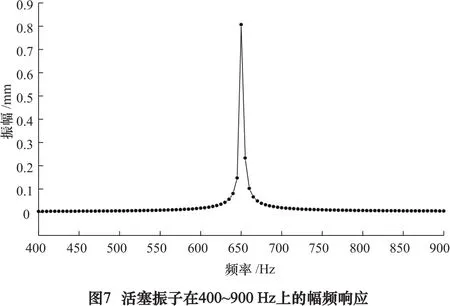
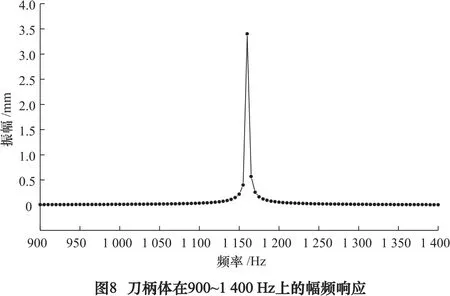
由图可见:在简谐载荷作用下新型刀柄在650 Hz和1 160 Hz两个频率点上分别引发活塞振子和刀柄体的共振。

2.2 与HSK-A63的谐响应对比

在HSK-A63模态分析的基础上对刀柄施加同一简谐载荷F(t)，扫描频率为0～1 500 Hz。计算提取刀柄体载荷作用点处在900～1 500 Hz上的幅频响应，并与新型高速刀柄对比，结果如图9所示。

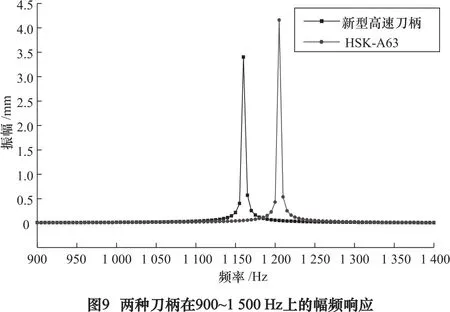
由图9可见:两种刀柄幅频响应极其相似，新型刀柄的固有频率略低，为1 160 Hz，共振幅值略小，为3.3 mm；HSK-A63刀柄的固有频率为1 205 Hz、共振幅值4.3 mm。新型刀柄具有良好的动态特性。

3 补偿系统液压油对刀柄动态性能的影响

3.1 模态对比

提取新型刀柄无液压油时的前六阶模态，结果见图10和表3。

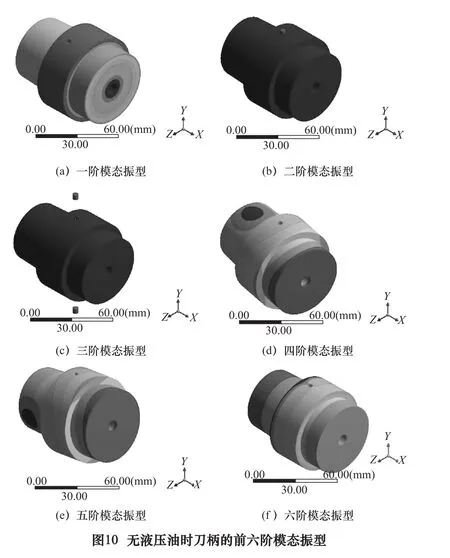
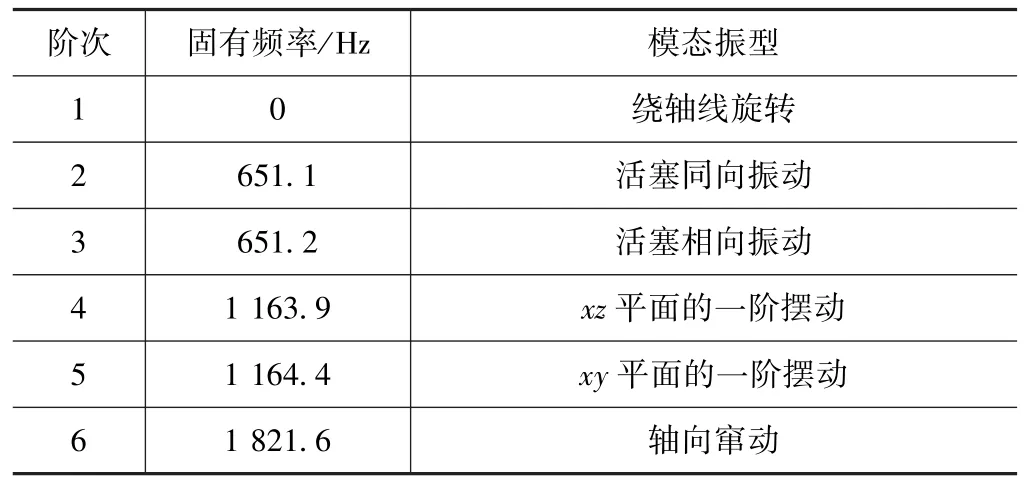
表3 刀柄的前六阶固有频率 Hz

由图表可见:对于新型刀柄和无油刀柄两种情况，活塞振子和刀柄体的固有频率和模态振型几乎完全相同，表明液压油对刀柄模态未产生影响。

3.2 谐响应对比

提取简谐载荷作用下活塞振子和刀柄体的幅频响应，与新型刀柄对比。结果如图11和图12。

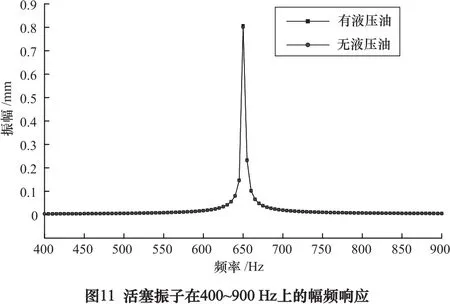
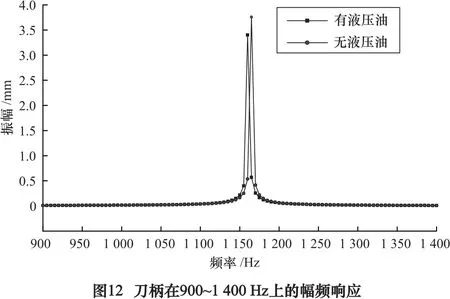
由图可见:(1)两种情况下活塞振子在400～900 Hz频段上的振动响应完全一致，表明液压油对活塞振子的受载振动没有影响。(2)相比无液压油，有液压油时刀柄体振动响应幅值稍小，说明液压油增加系统阻尼后增强了刀柄的抗振性。

4 结语

通过动态性能分析，得到如下结论:

(1)新型刀柄在其极限转速范围内不会引发系统共振。

(2)相较HSK-A63刀柄，新型刀柄具有较好的抗振性。

(3)系统内液压油对活塞振子的模态及受载振动均不会产生影响。液压油增大了刀柄阻尼，对刀柄抗振性能的改善起到一定作用。