基于查找表的彩色逆半调改进方法

李永前，张二虎

(西安理工大学印刷包装与数字媒体学院，陕西西安710048)

半调技术被广泛应用于印刷、出版及电子显示等领域，它是将连续调图像转换为二值图像的一项技术，转换后的二值图像在一定距离观察下可近似为连续调图像。由于半调图像仅包含0或1两个阶调,而现有的图像处理技术大多是针对连续调图像的，因此，如何实现半调图像的连续调恢复，即逆半调技术，成为了数字印前系统、半调图像转换加网、数字化档案管理、印刷图像分类识别等具体应用领域的重要研究课题。

逆半调技术的研究始于20世纪90年代[1]，按照其实现原理，可分为以下几类：滤波法、反褶积法、迭代法、机器学习法、矢量法等[2]。在现有的方法中，基于查找表(Lookup-table,简称LUT)的逆半调方法属于机器学习法[3]，它通过训练集建立半调图像值与连续调图像值之间的查找表，然后通过查表的方法重构出连续调图像。相对于其它逆半调方法，该方法充分利用了原有连续调图像特征以及先验知识，减少了逆半调图像信息的损失和信息失真度，而且这个方法可以分区并行操作，处理速度高于其他方法，所以具有更高的研究价值[4-6]。

基于LUT的逆半调方法的关键在于模板的设计与表中空值项的估计，模板的大小、形状以及模板中有效像素的相对顺序直接影响了图像的重建质量。近几年，国内外学者提出了多种改进的基于LUT的逆半调方法，如利用图像纹理信息、神经网络等改进的逆半调方法，但对直接影响逆半调图像质量的模板选择问题却很少研究。2001 年 Mese等[7,8]提出了一种基于贪心算法的模板选择方法，此后该模板的选择一直沿用该方法，但该方法并不能求得全局最优模板，存在一定缺陷。在空值项估计方面，提出的方法有低通滤波法、汉明距离法、最佳线性估计法[3]。2007年，孔月萍等[9]采用Elman神经网络方法进行了空值项估计的研究，取得了一定的改进效果，但估计精度仍然有待提高。

针对以上问题，本文提出了相应的改进方法。

首先，针对基于LUT逆半调方法恢复出的图像在平缓区域存在噪声的问题，提出基于查找表和基于高斯滤波相融合的方法，其框架如图1(a)所示。

图1 基于改进查找表和高斯滤波相融合的方法Fig.1 Method based on improved LUT and Gaussian filter fusion

其次，针对最优模板的选择问题，提出了基于粒子群的最优模板优化方法。

最后，采用超限学习机(Extreme Learning Machine,简称ELM)[10,11]作为空值项拟合模型，以提高空值项的拟合精度。

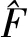
1 基于ELM的空值项拟合方法

经典LUT逆半调方法的原理如图2所示，它以多组半调图像及其连续调图像作为学习样本，学习之后形成一张半调模式值与连续值之间的映射表，从而可根据该映射表来估计半调图像对应的连续值，完成半调图像的逆半调处理。在图2中，对训练集中的半调图像，由任一像素点o′及其周围像素点a的不同组合可以形成不同的模板T1，典型的模板如图2(b)所示，其中模板的不同取值形成了图2(a)中LUT映射表的索引值，其在对应连续调图像中的值o作为LUT映射表的连续值V。

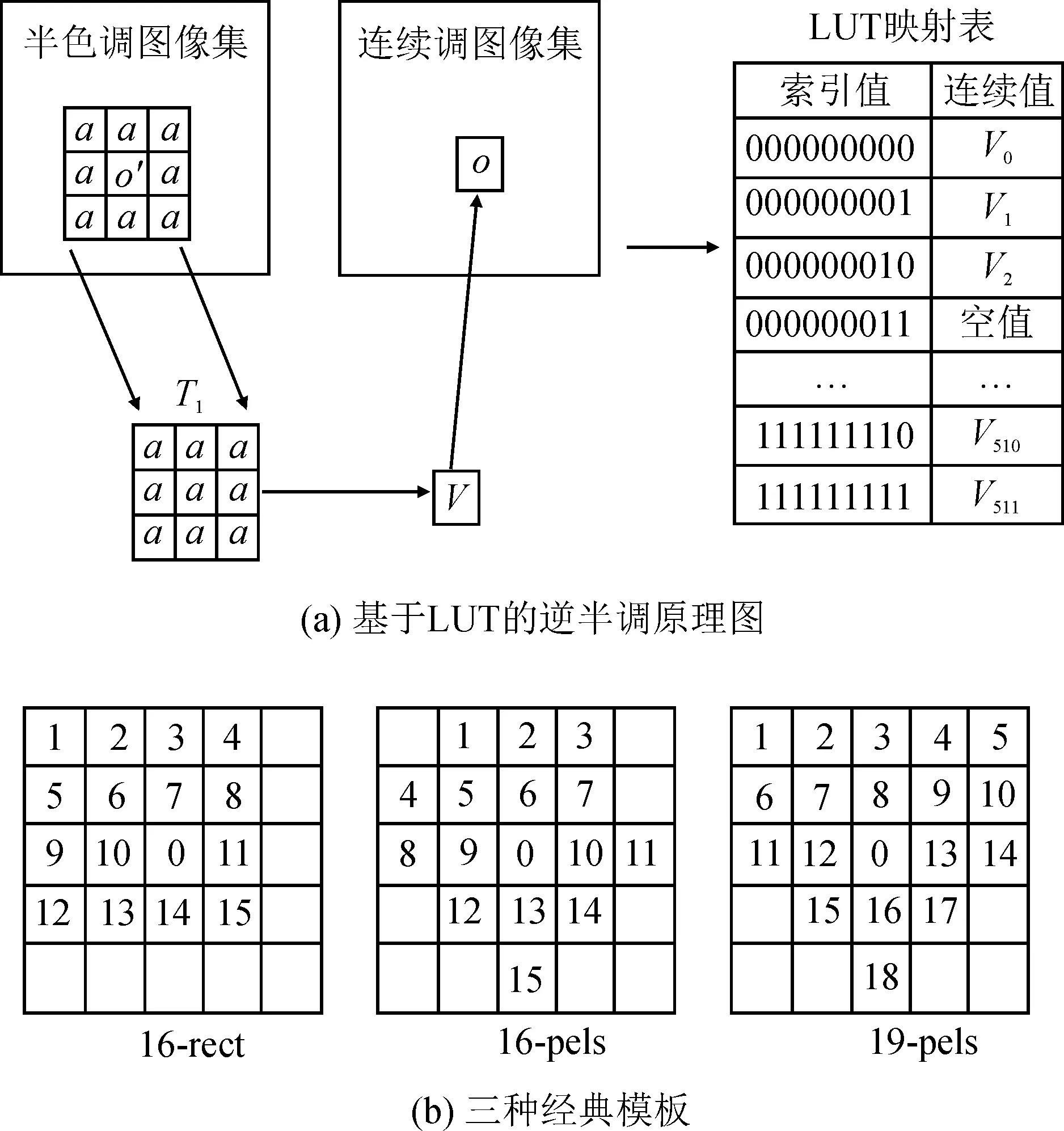
图2 经典LUT逆半调方法原理Fig.2 The principle of the classical inverse halftoning method based on LUT

经典LUT逆半调算法由建表和逆半调值生成两个阶段构成。建表阶段需要多组半调图像及其对应的连续调图像作为学习样本，利用模板滑动读取半调图像的模板像素值和对应的连续调值，建立初始的查找表。建表阶段有两种情况：一是相同的索引值对应不同的连续调值，对此采用这些不同连续调值的均值作为该索引值对应的连续调值；二是学习样本有限时，许多索引值没有其对应的连续调值，造成表中出现空值项的现象。对于空值项，提出基于ELM的空值项拟合方法，以提高拟合的精准程度。

超限学习机[10-11]是一种针对单隐藏层前馈神经网络的算法，其网络结构如图3所示，其中输入层X={x1,x2, …,xl}与隐藏层的连接权值W以及偏置b是随机产生，在训练过程中无需调整，只需要对隐藏层与输出层Y之间的连接权重β进行训练学习(可利用广义逆完成隐藏层与输出层的连接权重矩阵的求解),故ELM具有较快的学习速度、良好的鲁棒性和泛化能力、较高的拟合精度。在所设计的ELM网络结构中，以初始建立的LUT中非空值项数据训练ELM模型，其中输入X为LUT中的索引值，输出只有一个节点，为LUT中的连续调值y0，隐藏层节点数为50 。构建ELM空值项拟合模型：

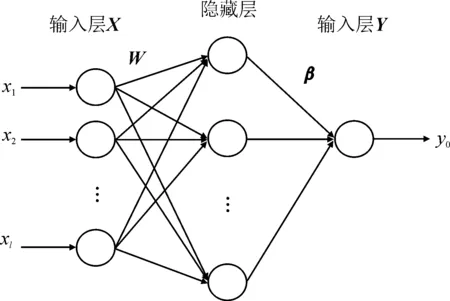
图3 ELM 网络结构Fig.3 ELM network structure

(1)

式中，“*”代表卷积运算符；g(x)为激活函数，常用硬限幅函数、Sigmoid函数或傅里叶函数，通过实验比较逆半调图像的效果，选择Sigmoid函数作为激活函数，其计算公式为：

(2)

实验中，提取初始LUT中非空值项的索引值和对应的连续值作为输入层和输出层样本，按照训练样本和测试样本数量比为9：1，对隐藏层与输出层的连接权重进行学习，完成基于ELM空值项拟合模型参数的求解。对于LUT表中的空值项，将其索引值作为输入层，利用训练好的ELM空值项拟合模型，就可估计出对应的连续值，从而得到完整的LUT映射表。

2 基于粒子群的最优模板优化方法

在基于LUT的逆半调方法中，形成索引值的模板设计非常重要，模板的大小和其中有效像素数目与LUT的长度成正比关系，与模板优化运行效率成反比关系，而且直接影响着逆半调图像的质量[12]。如何求取全局最优的模板是当前该领域研究的一个重要问题，文中采用粒子群优化方法，构建了一种最优模板。

粒子群优化算法(Particle Swarm Optimization，简称PSO)的基本核心是利用群体中的个体对信息的共享，使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。基于粒子群的最优模板优化方法步骤为：

1) 初始化粒子种群

由于LUT最优模板选择是一个非连续的问题，因此要先对粒子群算法的初始种群T进行随机编码。在编码时，针对有效像素数目为M的LUT表中的模板，可看作在N×N的窗口中选取M个位置。首先，模板中心点的目标像素位置选定为“0”；其次，模板的其他位置随机赋值为1～(N2-1)，而数值为0～(M-1)的位置即为LUT模板的有效像素。对于编码的顺序，从模板左上角开始，按照自左向右、自上而下的顺序对LUT模板进行扫描，得到种群个体。例如，N为5、M为16时，由于目标像素 “0” 位置不变，所以只需要1～24的位置，就可形成不同的模板，编码得到粒子个体的过程如图4所示。

图4 一个LUT模板编码过程Fig.4 A LUT template encoding process

2) 计算个体的适应度值

峰值信噪比(PSNR)是评价重建图像质量的最常用的指标。由于逆半调与图像压缩编码均涉及重建问题，故用峰值信噪比作为计算适应度的函数：

(3)

3) 更新粒子个体

在计算完当前粒子种群T的适应度后，首先比较选出当前种群中的最大适应度作为个体最优Pbest和全局最优Gbest；然后对当前粒子种群进行交叉和变异操作，产生新的种群T，使种群进化。交叉和变异的具体操作为：

① 交叉操作

交叉操作产生新种群分为两个阶段：一是与个体最优进行交叉；二是与全局最优进行交叉。首先，在Pbest/Gbest产生交叉位，交叉位的起始位置及长度均为随机获得，提取出交叉位上的数字，如图5中Pbest/Gbest红色标记出的14、9、22、3、4；然后对当前粒子个体，删除与交叉位上相同数字的元素，如图5中“粒子个体”中红色标记出的元素；最后，将剩余的元素按照相对位置不变依次排列，得到新的粒子个体，并将交叉位的元素插入到新的粒子个体最后，保证粒子个体的数目不变(如图5中“新的粒子个体”中红色标记出的元素)。

图5 交叉过程Fig.5 Cross process

②变异操作

首先，随机产生变异位c1、c2，其值在1到N2-1之间，而且c1和c2不能相同；然后对变异位c1和c2的元素进行交换，产生新的粒子个体。变异过程如图6所示。

图6 变异过程Fig.6 Variation process

对于更新后的粒子种群，计算其中各个个体的适应度，选出当前种群中的最大适应度作为个体最优Pbest，比较当前个体最优和上代个体最优，取最大的适应度作为当前全局最优Gbest。

4) 终止条件

通过实验，设定最大进化次数gMAX，当达到最大进化次数时，优化结束。

实验中设置最大进化次数gMAX=150，种群数目为20。考虑到LUT的大小及运行效率，选择模板大小N=5，模板中有效像素点数目M=16。

3 逆半调图像的融合

基于LUT的逆半调方法产生的连续调图像具有较好的细节保留能力，但在图像平缓区域容易产生噪声，而高斯滤波可起到平滑的作用，为此，提出将基于查找表和基于高斯滤波的逆半调图像进行融合。

3.1 基于高斯滤波的逆半调方法

高斯滤波是一种适用于消除高斯噪声的线性平滑滤波，可以消除数字半调图像中的噪声，获得具有较好平滑区的高斯逆半调图像IG(x,y) ：

IG(x,y)=(G*IH)(x,y)

(4)

式中，IH为数字半调图像；G表示高斯核函数；(x,y)表示目标像素。

3.2 逆半调图像的融合

通过基于PSO算法得到的最优模板建立初始LUT，由ELM完成空值项拟合，通过查表的方式获得基于LUT的逆半调图像IL(x,y)，将其与高斯滤波获得的逆半调图像IG(x,y)进行融合，得到最终的逆半调图像I(x,y)，该方法简称基于融合的算法，其公式为：

I(x,y)=w(x,y)IL(x,y)+[1-w(x,y)]IG(x,y)

(5)

w(x,y)=tanh(vL(x,y)/θ)

(6)

式中，w(x,y)为融合的权值系数；θ为正值参数；vL(x,y)是以目标像素 (x,y)为中心的n×n区域的方差，取n=5。使用tanh 函数既可以保证融合的权值系数在0～1之间，而且可以区分出图像的细节和平滑区域。

3.3 彩色半调图像的逆半调方法

大多数的彩色图像半调处理是对色彩空间内图像所具有的各个颜色通道分别进行处理，然后再将各通道结果叠加得到彩色半调图像。对于彩色图像逆半调，本文也是将彩色半调图像的R、G和B三个颜色通道分别进行逆半调处理，实现彩色半调图像的逆半调化。

4 实验结果与分析

本节对所提出的基于ELM的空值项拟合、基于PSO的模板优化和逆半调图像融合进行实验，实验全部在Matlab R2014a环境下完成。

4.1 基于ELM的空值项拟合实验

本小节的实验图像均为灰度图像，首先由15对大小为512×512的误差扩散半调图像和对应的连续调图像集作为训练样本，完成初始LUT表的建立及基于ELM的空值项拟合模型的建立，LUT表的模板采用16pels的形式；然后由8对大小为512×512的误差扩散半色调图像和对应的连续调图像集作为测试样本，采用PSNR对生成的逆半调图像质量进行评价。

对ELM中采用的不同激活函数进行实验，实验结果如表1所示，表1给出的是测试样本的平均PPSNR值。从表1的PPSNR值可以看出，采用Sigmoid激活函数具有最好的效果。

表1 不同激活函数得到的PPSNR值

对于空值项的拟合精度，采用平均相对误差(Average Relative Error，简称ARE)进行评价，其计算公式为：

(7)

式中，u表示图像中空值项数；IZ表示图像中空值项的真实连续调值；IN表示空值项的拟合值。

表2给出了8幅测试图像的空值项数和平均相对误差值。从表2可以看出，每幅测试图像都有较多的空值项，拟合后的空值项的平均相对误差都在0.1左右，说明ELM拟合达到了较高的精度。

表2 测试图像拟合值的平均相对误差

4.2 求取最优模板的算法比较

为了提高训练与测试的速度，实验采用灰度图像。训练样本为15对大小为512×512的误差扩散半调图像和对应的连续调图像集，测试样本为8对大小为512×512的误差扩散半调图像和对应的连续调图像集，训练样本和测试样本互不相同。

为体现PSO算法的优势，同时采用差分进化算法[12](Differential Evolution Algorithm，DE)、精英遗传算法[13](Elitist Genetic Algorithm，EGA)求取最优模板，并对比其结果。实验中各种算法的最大进化次数均为150，种群规模均为20。

图7是各算法的收敛速度，可以看出，本文提出的基于PSO算法的收敛速度最快，其次是DE算法和EGA算法。图8是各算法求得的模板，其中图8(b)和(c)是实现文献[12]和[13]算法得到的最优模板，图8(a)是PSO算法求得的最优模板，它与另外两个最优模板相近，但是更能体现有效像素相对顺序的影响。表3给出的是由不同模板生成的逆半调图像的平均PPSNR值，可以看出，本文PSO算法获得的最优模板是最好的。

图7 各算法进化次数与PPSNR关系Fig.7 Relationship between the evolution times and PPSNR of each algorithm

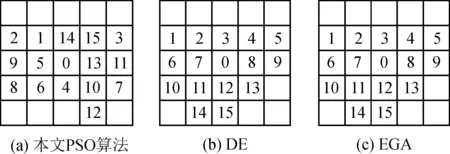
图8 各算法求得最优模板Fig.8 The best template of all algorithms

算法PPSNR/dB本文PSO算法30.054DE算法[12]29.294EGA算法[13]29.294

4.3 彩色逆半调图像效果评价

实验中学习样本为60对大小为256×256的彩色误差扩散半调图像和相应的连续调图像集，测试样本为10对大小为256×256的彩色误差扩散半调图象和相应的连续调图像集，学习样本和测试样本互不相同。 实验首先确定相关参数，然后对最终生成的彩色逆半调图像质量进行评价分析。

图9是学习样本数量对逆半调图像质量的影响。实验中学习样本的数量S从15变化到60，变化的步长为5，测试样本数量为10。从图9可以看出，当学习样本数量逐渐增加到50时，平均PPSNR值是逐渐增大的，超过50时，平均PPSNR值减小，故选择学习样本数量为50。

图10 是高斯滤波逆半调处理中参数σ的选择实验。σ值从0.6变化到2.4，变化步长为0.2，计算10对测试样本的平均PPSNR值作为评价标准。从图10 可以看出，σ=1.2时平均PPSNR值最大。

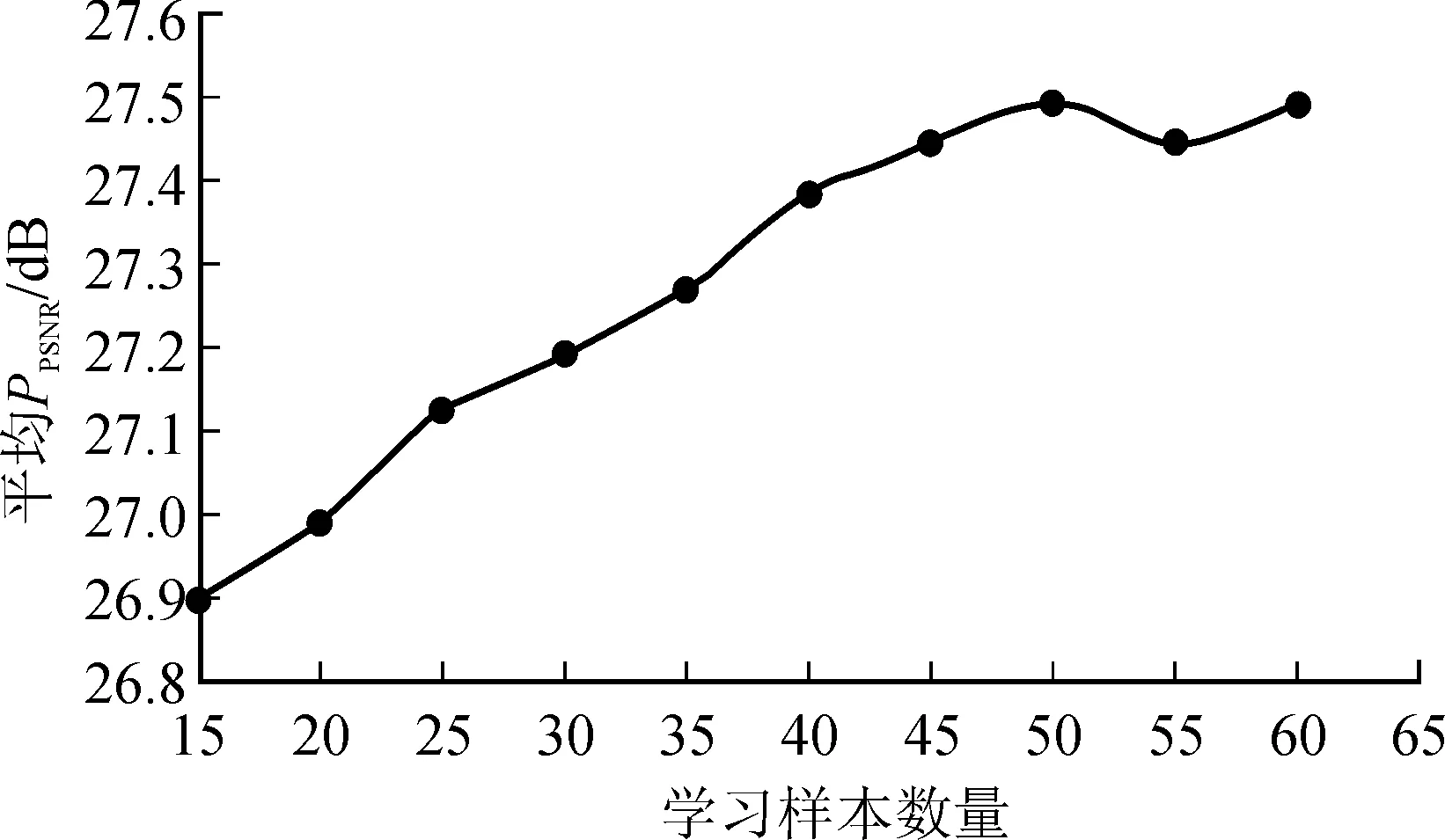
图9 学习样本数量与平均PPSNR的关系Fig.9 Relationship between the number of learning samples and the average PPSNR

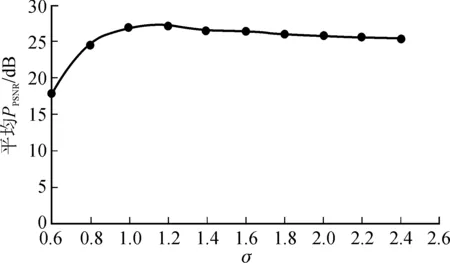
图10 σ 与平均PPSNR的关系Fig.10 Relationship between σ and average PPSNR

对于式(6)中θ的取值，图11给出了参数θ从100变化到5100，变化步长为100时，10对测试样本平均PPSNR值随θ变化的情况。可以看出，随着θ值的增大，平均PPSNR值逐渐增大，当达到5000时基本趋于稳定。

根据以上实验，最终选择的参数为S=50、σ=

1.2、θ=5000。在这组参数下，实验对4种方法生成的彩色逆半调图像的质量进行评价。

表4给出了各种方法的实验结果，其中“LUT(空值未补)”表示基于LUT逆半调方法，空值项未作处理；“LUT(ELM补全空值)”表示基于LUT逆半调方法，空值项由ELM拟合。表4给出的是10幅彩色逆半调图像的平均PPSNR值，从表中可以看出，本文基于融合的算法是最优的，取得了最高的PPSNR值。

图11 θ与平均PPSNR的关系Fig.11 Relationship between θ and average PPSNR

算法PPSNR/dBLUT(空值未补)26.296LUT(ELM补全空值)27.492Gaussian滤波法26.046本文基于融合的算法31.115

图12给出了一幅用于测试的彩色半调图像由不同方法处理的结果。

图12 各种不同算法的处理后的彩色图像比较Fig.12 Comparison of inversed color image restored by different algorithms

从视觉效果来看，图12(c)LUT(空值未补) 方法恢复出的图像达到了一定的去噪效果，但是有较明显的白色斑点；图12(d)LUT(ELM补全空值)方法恢复出的图像在眼睛部分的瞳孔和瞳仁处有很高的区分度，但是仍有较不明显的白色斑点，且在图像的平缓区域存在着均匀分布的噪声；图12(e) 基于Gaussian滤波方法恢复出的图像虽然有较好的平滑效果，但该图像的细节部分却没有图12(d)好，眼睛部位较模糊，区分度不高；图12(f) 是文中所提基于融合的方法恢复出的图像，可以看出，其与原连续调图像有较高的相似度，人物的头发和眼睛部位等细节处有较高的还原度，且滤除了平缓区域的噪声及其它的斑点，取得了最好的视觉效果。

5 结 论

本文提出了一种改进的基于查找表的彩色逆半调方法，其改进之处包括：

1) 采用基于粒子群的优化方法获得了最优模板，并与差分进化算法、精英遗传算法进行比较，结果表明,本文算法求得的最优模板对半调图象恢复有更好的效果，求得的最优模板更加符合数字图像像素之间的相关性，而且较其它两种算法有更快的收敛速度；

2) 提出了基于ELM的空值项拟合方法，有效地消除了恢复图像中的斑点；

3) 提出了一种融合LUT逆半调图像和高斯滤波逆半调图像的算法，在保留图像细节的同时去除了平缓区域的噪声，在客观评价和主观评价方面均取得了最好的效果。