题不在多 但求精彩——例谈“1+3 作业模式”习题精选和设计的策略

浙江省江山市城南中学 陈立顺

做习题，是学生重温和组合旧知，去解决“新”课题的过程，这个过程，也是学生经历观察、分析，并不断调整策略的过程。因此，做习题对训练学生的思维，提高学生的数学能力和素养至关重要。那么教师应怎样精选和设计习题，让学生摆脱“题海”，做到以少胜多呢？多年来，本人探索并践行了一种“1+3 作业模式”，即1 本省编作业本加上3 道提高题供学生分层作业。其设计策略主要体现在以下三个方面：

一、一题多解，旨在多解归一，凸显本质

例1 如 图1，AM ∥BN，求∠APB，∠PAM，∠PBN 三个角之间的数量关系（要求至少用三种不同的解法）。

分析：这道题得出三个角的和为360 度的结论并不难，难就难在要用多种方法求解。解法1：如图2，过P 作PQ ∥AM ，由平行线的性质和周角的意义可得结论；解法2：如图3，连接AB，由平行线的性质和三角形内角和性质可得结论；解法3：如图4，在BN 上任取一点Q，连接AQ，由平行线的性质和四边形内角和性质可得结论；解法4：如图5，作QR 与AM，BN 交于R，Q，由平行线的性质和五边形内角和性质可得结论；解法5：如图6，任意作截线QR 与AM，BN 所在直线交于R，Q，再用平行线的性质、三角形及四边形内角和性质也可获得结论。

图1

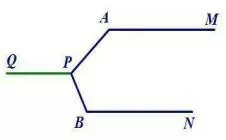
图2

图3

图4

图5

图6

当然解法远不止这些，但解题不应到此结束。一题多解之后要进行多解归一，归一才能凸显本质。上述解法虽然开始都不同，但走到最后，都需要应用平行线性质，可见通过构造截线或被截线，让两直线平行产生至少一对内错角或同旁内角或同位角，从而让两直线平行这个条件“英雄有用武之地”是必经之路。其次，从结论来看，添辅助线的目的也是为了把要求和的分散的三个角集中到所熟知的多边形或者周角、平角及互补的同旁内角这些基本图形中，从而解决问题。另外，从考查的知识看，构造的这些图形无非就是将平行线与各种多边形或周角等图形进行组合而已。学生这样做题，就可切入本质，深刻理解知识之间的联系，从而做到做一题，通一类，这也正是提升解题能力的根本之道！当然其前提是习题一定要精心选择和设计。

二、题组训练，旨在多题归一，揭示基本思考规律

例2 完成下列题组：

1.已知点A（3，7）、B（1，2） 、C （6，4）是坐标系中的三个点，点D 是平面上的另一点。若以点A，B，C，D为顶点的四边形为平行四边形，求点D 的坐标。

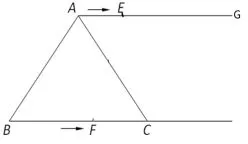
图7

2.如图7，正三角形ABC 的边长为 6 cm，射线AG ∥BC，点E 从点A 出发，沿射线AG 以1cm/s的速度运动，同时点F 从点B 出发，沿射线BC 以2 cm/s 的速度运动，问运动多长时间，以A，F，C，E 为顶点的四边形是平行四边形？

3.已知抛物线y=ax2+bx+c 过A（-1，0），B（5，0），C（0，5）三点。点M，N 分别为直线BC 和抛物线上的动点，若以M，N，C，O 为顶点的四边形为平行四边形，试求出点M 的坐标。

分析：平行四边形顶点坐标有如下规律：平行四边形相对顶点的横坐标的和相等，纵坐标的和相等。第1 题中三个顶点坐标是已知的，只要以相对顶点为线索，分三种情况讨论即可求得点D 的坐标。第2题中平行四边形两个顶点是定的（坐标未知），则可分别以AC 为对角线和边分两种情况进行分类求解： 先用时间t 表示出AE 和 CF，再根据AE=CF 列出方程求解。第3 题中平行四边形有两个顶点定（坐标已知），一种解法就是先设出定直线上点M 的坐标为（m，-m+5），然后以相对顶点为线索用m 表示出点N 的坐标，再代入抛物线的函数表达式进行求解。当然，这题还可以进行一题多变，将抛物线改成双曲线或圆或直线等。

上述题组旨在多题归一，揭示出如下动点形成平行四边形的基本思考规律：

1.变中抓不变，分析哪些顶点定，哪些顶点动；

2.若三定一动，则以相对顶点为线索分三种情况求解；

3.若两定两动，则分两种情况，一是两定点坐标已知，则可用一个字母先表示第三个顶点坐标，再以相对顶点为线索分三类求出第四个顶点坐标，再根据第四个顶点满足的条件进行求解。二是两定点坐标不易求得，则以两定点的连线段为抓手，分别以它为边和对角线分类进行求解……（此规律还要在实践中加以完善）

上述题组训练，关键在于教师能否引导学生总结出那些常用的基本图形、基本数式及基本思考规律等。

三、题型齐全，紧扣中考趋势，全面训练各类解题方法

从现行中考数学试卷结构看，有选择题、填空题和解答题三大题型。从具体题型看，有计算题、作图题、证明题、规律探索题、阅读理解题，新定义题及综合题等。每一类题型的解题方法也会有差异。特别是选择题和填空题，只求正确结论，不必写出步骤，因此解题策略就显得非常重要。教师要引导学生充分利用题目的有效信息选择恰当的方法进行 “巧算”，其主要解法有直接法、猜想法、特殊值法、枚举法、数形结合法、代入验证法、排除法、实践操作法、测量法和估算法等。当然，有时解一道题需同时使用几种方法，教师要精选好习题，让学生平时加以训练。

总之，题不在多，但求精彩。只有教师科学地精选和设计习题，才能让学生做到以少胜多，举一反三，从而切实减轻学生的学业负担，让学生全面健康地成长。