高中数学不等式高考试题分析与教学策略

山东省临沂第四中学 郭娟娟

不等式直观反映了事物在量上的区别，是研究数量关系的重要途径。而且不等式与其他知识联系密切，能广泛运用于集合、函数、方程、概率等相关数学知识中，可以说是学生学习其他数学知识的基础。与此同时，高考数学中不等式题目不仅注重学生不等式相关知识的掌握，更加注重学生数学逻辑思维、推理思维、抽象思维及数学思维能力的考查，因此高中数学教师必须要对高考数学中的不等式试题进行全面的分析，并从高考题出发探寻科学、有效的教学策略，以提升和优化学生不等式学习效果。

一、注重不等式解法的探索，增强学生思维能力

解不等式是不等式知识的基础内容，学生只有牢固掌握了解不等式的知识内容，那么不等式问题便可以迎刃而解。所以高中数学教师必须要以各类往年高考数学不等式真题出发，引导学生从实际问题中理解不等式成立的条件、不等式所具备的工具性、单向性、双向性等性质，更要加强不等式与函数、方程、数列、几何以及实际应用问题的联系，让学生探索各种不等式题目的解法，逐步形成过程意识，并体会不同的数学思想方法，从而增强学生的思维能力。

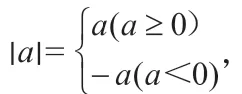
二、通过观察推理论证过程，培养学生抽象思维

不等式的证明和推导过程也是数学高考题中对不等式知识考查的主要内容和形式之一，因此，高中数学教师要在实际过程中加强不等式的观察推理和论证过程，有效培养学生的逻辑推理等抽象思维能力。具体来说，数学教师要引导学生观察基本不等式的推导证明过程，让学生从整个推理论证过程中更加深刻地理解不等式知识和内容，并能够让学生体会其中所蕴含的数学思想方法，从而有效培养学生的逻辑推理能力和抽象思维能力，为学生良好解决问题能力的提升奠定基础。

例如，为了培养学生的抽象思维，笔者以“使不等式|x-4|+|x-3|＜a 有解，那么a 的取值范围为多少”这道例题为例，引导学生通过观察推理，论证不等式的解题过程，首先，笔者先为学生画出数轴，然后将数轴分为（-∞，3]，[3，4]，（4，+∞]三个区间，分好区间后，笔者再引导学生根据这三个区间进行分段分析，如，当x＜3 时，原不等式变为（4-x）+（3-x）＜a，最后求出a＞1；当3 ≤x ≤4 时，a＞1；当x＞4 时，a＞1。以上三种情况中的任一种均满足题目要求，所以取它们的并集，即a＞1。这样，在高中数学不等式高考试题的讲解中，笔者通过引导学生观察推理论证的过程，有效培养了学生的抽象思维。

三、设置典型问题，引导学生发现问题本质

问题是教学活动中最有效的因素，同时也是高考中对数学不等式知识考查 的主要形式，因此，高中数学一定要基于高考题的基本特性和不等式知识的基本内容来精心设计典型数学问题，并以启发、引导的方式向学生提出问题，调动学生的思考动机，激发学生的求知欲和探究欲，使学生由被动学习变为主动学习，这时教师必须要抓住机会，引导学生发现问题的本质，逐步向不等式的灵魂和核心靠近，从而切实提高学生解决问题的能力，能够灵活应对和解答各种不等式问题。例如，在讲解不等式类型的高考题时，为了引导学生发现问题的本质，笔者围绕求解不等式的条件为学生提出问题，如哪些类型的题涉及绝对值，哪些类型的题是综合型例题。

总之，不等式是高考数学的重要考点之一，分析高考数学中的不等式试题并基于此优化高中数学不等式教学是课程改革与高考改革的必然要求，更是保证学生学习效果的重要途径。因此，高中数学教师要通过注重不等式解法探索、观察推理论证和设置典型问题等途径来优化不等式教学，提高不等式教学的效率和质量，进而提高学生数学思维能力和分析问题解决问题的能力，让学生能真正理解不等式，灵活应对各种高考题。