三角函数常见典型考题赏析

■黄林平

三角函数是高中数学的基础知识之一，同学们要理解其定义，掌握三角公式的灵活运用。下面就三角函数常见的典型考题进行举例剖析，供大家学习与提高。

题型1：角的集合表示及象限角的判断

利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数赋值来求得所需角。利用终边相同的角的集合S=｛β|β=2kπ+α，k∈Z｝判断一个角β所在的象限时，只需把这个角写成[0，2π）范围内的一个角α与2π的整数倍的和，然后判断角α所在的象限。

例1集合中的角所表示的范围（阴影部分）是（ ）。

解：当k=2n（n∈Z）时此时α表示的范围与表示的范围一样；当k=2n+1（n∈Z）时，2nπ此时α表示的范围与表示的范围一样。应选C。

跟踪训练1：点A（sin2018°，cos2018°）在直角坐标平面上位于（ ）。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

提示：由sin2018°=sin218°=-sin38°＜0，cos2018°=cos218°=-cos38°＜0，可知点A（sin2018°，cos2018°）在第三象限。应选C。

题型2：扇形的弧长、面积公式的应用

例2一个半径为R的扇形，它的周长为4R，则这个扇形所含弓形的面积是（ ）。

D.R2（1-sin1·cos1）

解：设圆心角为θ。

跟踪训练2：如图1，已知扇形OAB和OA1B1，A1为OA的中点，若扇形OA1B1的面积为1，则扇形OAB的面积为_____________。

图1

提 示：设 ∠AOB=α，则

因 为 OA=2OA1，所 以 S扇形OAB=

题型3：三角函数的定义问题

三角函数定义问题的常见类型及解题策略：（1）已知角α的某个三角函数值，求角α终边上一点P的坐标中的参数值，可根据定义中的两个量列方程求参数的值。（2）已知一个角的三角函数值（sinα，cosα，tanα）中任意两个的符号，可分别确定出角终边所在的可能位置，两者的交集即为该角终边的位置，这时要注意终边在坐标轴上的特殊情况。

例3若角α的终边在直线3x+4y=0上，求sinα，cosα和tanα的值。

解：对于含有参数的三角函数求值问题，一定要考虑运用分类讨论的思想方法。

设α终边上任一点为P（-4a，3a）。

跟踪训练3：已知角α的终边经过点P（x，且求的值。

题型4：关于sinα，cosα的齐次式问题

形如asinα+bcosα和asin2α+bsinα·cosα+ccos2α的式子分别称为关于sinα，cosα的一次齐次式和二次齐次式。对于涉及它们的三角变换问题，通常转化为正切值（分子、分母同除以cosα或cos2α）求解。

例4已知

（1）求sinx-cosx 的值。

解：（1）（方法1）由题意可得方程组

消去sinx后整理可得25cos2x-5cosx-12=0。因 为所以可得

跟踪训练4：已知sinαcos则cosα-sinα的值为（ ）。

提示：由可得cosα＜0，sinα＜0，且|cosα|＜|sinα|，所以cosα-sinα＞0。又（cosα-sinα）2=1-2sinαcosα=1-2所以cosα-sinα=应选B。

题型5：三角函数的奇偶性、周期性和对称性问题

例5已知函数f（x）=sin（ωx+φ）的最小正周期为4π，且对∀x∈R，有恒成立，则f（x）图像的一个对称中心是（ ）。

解：由f（x）=sin（ωx+φ）的最小正周期为4π，可得因为恒成立，所以即+2kπ（k∈Z）。由可得故

跟踪训练5：已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）为奇函数，该函数的部分图像如图2所示，三角形EFG是边长为2的等边三角形，则f（1）的值为（ ）。

图2

提示：由f（x）=Acos（ωx+φ）为奇函数，可得f（0）=Acosφ=0。因为0＜φ＜π，所以这时f（x）=-Asinωx。

题型6：三角函数的单调性与最值问题

求形如y=Asin（ωx+φ）+k的单调区间时，只需把ωx+φ看作一个整体代入y=sinx的相应单调区间即可（若ω为负数，则要先把ω化为正数再代入）。求较为复杂的三角函数的单调区间时，先化简成y=Asin（ωx+φ）的形式，再求y=Asin（ωx+φ）的单调区间。

例6函数[-2π，2π]的单调递增区间是（ ）。

B

解：依题意可得当即时，函数y=是单调递增函数。由于x∈[-2π，2π]，因此函数的 单 调 递 增 区 间 是应选D。

跟踪训练6：设ω是正实数，函数f（x）=2cosωx在上是减函数，那么ω的值可以是（ ）。

提示：因为函数f（x）=2cosωx 在上单调递减，所以要使函数f（x）=2cosωx（ω＞0）在区间上单调递减，则即所以解得故ω的值可以是应选A。

题型7：“五点法”作图及图像变换

函数y=Asin（ωx+φ）（A＞0，ω＞0）的图像作法：（1）用“五点法”作y=Asin（ωx+φ）的图像，可设z=ωx+φ，由z取来求出相应的x值，通过列表，计算得出五点坐标，描点后得出图像。（2）由函数y=sinx的图像通过变换得到y=Asin（ωx+φ）的图像，有两种主要途径，即“先平移后伸缩”与“先伸缩后平移”。

例7已知曲线C1：y=cosx，C2：y=则下面结论正确的是（ ）。

A.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2

B.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2

C.把C1上各点的横坐标缩短到原来的纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2

D.把C1上各点的横坐标缩短到原来的纵坐标不变，再把得到的曲线向左平移

个单位长度，得到曲线C2

解：y=sin由y=cosx的图像得到y=cos2x的图像，需将曲线C1上各点的横坐标缩短到原来的纵坐标不变；由y=cos2x的图像得到的图像，需将y=cos2x的图像上的各点向左平移个单位长度。应选D。

跟踪训练7：将函数f（x）=-cos2x的图像向右平移个单位后得到函数g（x）的图像，则函数g（x）（ ）。

题型8：利用图像求解析式y=Asin（ωx+φ）+B（A＞0，ω＞0）的方法

例8已知函数y=Asin（ωx+φ）+b的最大值为4，最小值为0，最小正周期为直线是其图像的一条对称轴，则下面各式中符合条件的解析式为（ ）。

解：由函数y=Asin（ωx+φ）+b的最大值为4，最小值为0，可知b=2，A=2。由函数的最小正周期为可知得ω=4。由直线是其图像的一条对称轴，可知即可得φ=故满足题意的函数为2。应选D。

跟踪训练8：函数f（x）=2sin（ωx+φ）的部分图像如图3所示，则ω，φ的值分别是（ ）。

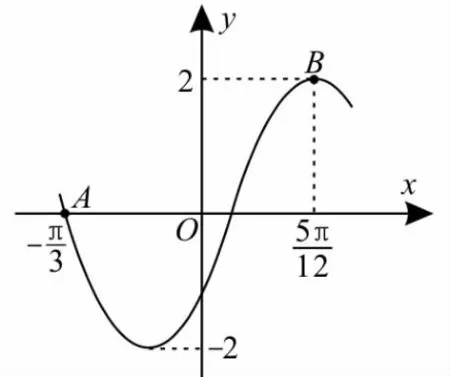
图3

提示：由题意及图像可知可得T=π，所以ω=2。因为图像过点所以Z），即又所以应选A。