美不胜收的图形

说到美，人们的第一反应就是，音乐中动人的旋律，美术中明快的色彩，让人感觉好像与数学没有一点关系。其实，纵观小学数学，几何图形的美无处不在。蔡元培说：“几何学各种线体，可以资美育。”那么，在小学数学中，几何图形究竟蕴含了哪些美呢？笔者将从以下几个方面进行阐述。

一、图形的对称美

对称是指图形或事物对某点、某直线或某平面而言，在大小、形状或排列上具有一一对应的关系。对称性是数学美最重要的特征，是数学家追求的最终目标，也是数学发现与创造中非常重要的美学因素。著名德国数学家和物理学家魏尔说：“美和对称紧密相连。”可以说，现实生活中处处有对称，既有轴对称、中心对称等空间对称，又有周期、节奏和旋律等时间对称，还有与时空坐标无关的更为复杂的对称。

孩子们最早认识对称是从“圆”开始的，正如毕达哥拉斯所说：“一切平面图形中最完美的是圆。”正是因为圆是沿任意一条直径所在的直线成对称的，又按圆心成中心对称，所以我们认为圆的对称是最完美的。像线段、长方形、正方形、等腰三角形、等腰梯形等，这些简单的对称图形还可以通过平移和旋转，演变成各种各样的组合图形，而且还具有对称这一特性。

在小学数学中，一些几何体也具备对称性。球一向被认为是最简洁美丽的几何体，它呈中心对称，而且所有对称中心的截面都是另一种比较完美的对称图形——圆。当然，具备对称美的几何体还有长方体、正方体、圆柱、圆锥、旋转曲面、椭球面等，这些图形都有对称性，直观地给人以美的享受，所以在日常生活中用途非常广泛。许多建筑师和美术工作者经常采用一些对称图形，设计出漂亮的装饰图案，也让我们更加深刻地感受到，人们可以通过图形的对称美，为我们的生活增添许多魅力。

二、图形的简洁美

爱因斯坦说过：“美，本质上终究是简单性。”他还认为，只有借助数学，才能达到简单性的美学准则。物理学家爱因期坦的这种美学理论，在数学界，也被绝大多数人所认同。朴素，简单，是其外在形式。只有既朴实清秀，又底蕴深厚，才可以当真无愧为至美。

图形几何方面的知识最显著的特征是简洁美。公式的推导力求讲究简洁；公式的表述力求简明；几何公式的应用要求尽可能简化。例如，在教学角的概念时，教材中给出的定义是：从一点引出的两条射线。而射线这个概念也是直接引用，并没有其他的说明。

数学基本概念、理论或公式所呈现的简单性便是一种实实在在的简洁美，使学生学得既轻松又有味。例如，圆的周长公式：C=2πr，就是“简洁美”的典范。一个如此简单的公式，概括了一切圆形的共同特性，怎不令人惊叹不已？在数学中，像周长公式这样形式简洁、内容深刻的公式、定理还有很多。

其实，数学的简洁美，只用几个定理是不足以说明白的，数学历史中每一次进步都使已有的定理更简洁。正如希尔伯特所说：“数学中每一步真正的进展，都与更有力的工具和更简单的方法的发现密切联系着。”

三、图形的和谐美

在图形与几何知识教学时，通过操作、观察、度量、绘制等，让学生感悟到直线美、曲线美、平面图形美以及立体图形美，并在它们中寻找到组成图形的部分和部分之间、整体和整体之间的一种统一和谐美。

如下图所示：圆与其他图形组合在一起，给我们一种多样统一的和谐感。

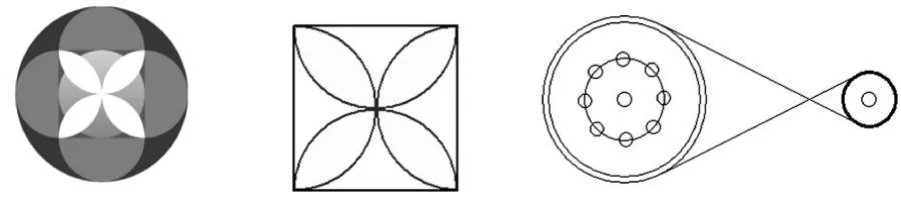
在以上这些图形的变化时，让学生欣赏这组优美的图案，从图案中找出最基本的图形，再认真观察图案是怎样由基本的图形变化而成的，从而体会到通过旋转、平移这两种最基本的变化就能创造出许多漂亮的图案。接着引导学生发挥想象力，用更多的基本图形组合设计一幅图案，并配上解说词。学生的想象力特别丰富，不但设计出常见的如小鸟、电灯、棒棒糖、小树等事物，而且设计出踢足球的人，被打爆的脸，生气的猪等图案，形象生动鲜明，这种活动不仅让学生爱上数学，更让学生体会到数学的和谐美，提升他们的审美品味，激发他们去创造美。

四、图形的奇异美

奇异美也是几何图形的一个基本特征，它会给人一种妙不可言的感觉。既包含方法上的新颖、奇巧；又有结果上的出乎意料，往往能勾起我们思想上的震动，引起我们的赞赏与叹服。

例如：教学平面图形的计算公式时，可以把平行四边形割补成长方形来计算；把两个完全一样的三角形拼成一个平行四边形来计算；把两个完全一样的梯形拼成一个平行四边形来计算；把圆割补成近似的长方形来计算等。这种在动手操作中所蕴含的巧妙方法以及产生的奇异结果，让学生在惊叹中感受到美的熏陶，在以后的学习中产生向往奇异的数学思想与方法。

其实，很多组合图形在进行面积计算时，大多采用了不同的变换方式，如割补或平移等巧妙的方法，将其转化成规则的简易图形进行计算。发展了学生的创新思维，培养了学生的创新能力。

总之，几何图形中的美无处不在，数学中的美更是数不胜数。只要我们拥有一双慧眼，就能发现数学的美，如果引导孩子从小在数学学习过程中去探索、去发现数学之美，欣赏数学美的魅力，最终用数学中各式各样的美来提升学生的审美情趣，激发他们的学习兴趣。