论希格斯机制实在论理解的必要条件
曹天予/文,王伟长/译
(波士顿大学 哲学系,美国 马萨诸塞州波士顿市 02215)
一、导言
最近在欧洲核子研究中心的大型强子对撞机由ATLAS和CMS实验发现的一种有质量的标量粒子——最先由彼得·希格斯在一篇讨论对称性破缺的文章[1]中提出,自此就被称为希格斯玻色子——是粒子物理具有重大意义的一个进展①。但是,希格斯粒子究竟有多大的意义,这个问题是依赖于解释的。一个通常的估计是它确证了一种机制——最先由Francois Englert和Robert Brout在BrokenSymmetryandMassofGaugeVactorMesons[2]一文中提出,并由彼得·希格斯在SpontaneousSymmetryBreakdownwithoutMasslessBosons[3]一文中将其精细化——这种机制被认为对我们理解亚原子粒子质量的起源有所贡献。②然而,EBH机制究竟在何种意义上被观测③、确证——或者说被认为被确证(包括实际上到底是什么被确证)——并且这种机制在何种意义上对我们理解质量的产生④有贡献,这些问题关键性地取决于对这个机制的意义的理解。⑤这篇短文将通过对EBH机制的起源进行历史的考察(第2节)来澄清它的概念基础(第3节);接下来要通过对其基础(基本物理材料)的现实状态的考察来讨论的是该机制的本体论状态——是实在论的还是工具主义的(第4节);本文的结论是,在戈德斯通模式(Goldstone modes)的动力学特性的转变和物理自由度重组中的固定性这两个谜题得到妥善的解决之前,EBH机制的实在论状态将一直无法确定(第5节)。
二、EBH机制的起源⑥
历史上,EBH机制产生于围绕着以下三条发展线路:(1)简并的真空态中呈现的破缺的对称性;(2)有着对称性破缺解的标量场论;(3)使规范玻色子具有质量的机制。
随着始于20世纪50年代中期的发展——比如PCAC[全称Partial Conservation of Axial Current,是最先在弱相互作用的粒子流图景(current-current picture)中被采用的假设],樱井纯和谢尔顿·格拉肖提出的规范理论,SU(3)味对称性和流代数——粒子物理学家⑦越来越意识到对妥善理解对称性破缺的迫切需要。然而更加值得我们关心的是阿伯拉罕·派斯(Abraham Pais)早在1953年发现的分层次的(强相互作用、电磁相互作用和弱相互作用)并且对称性逐层减少的一系列相互作用。这一系列分层次的相互作用的见解和它们相关的对称性对海森伯在ResearchontheNon-linearSpinorTheorywithIndefiniteMetricinHilbertSpace[4]一文中提出的非线性统一场论是具有启发性的:如果他不能在具有多种对称性的多种相互作用中,从具有比现象本身所呈现的更高的对称性的潜在场的方程中推导出这些现象,那么他的统一理论就没有意义。也就是说,除非潜在理论的对称性通过这样或那样的方式发生破缺,不然理论就无法在有着较低对称性的各种相互作用中描述现象。⑧
朗道在1958年11月21日写信给海森伯支持他的统一理论,信中提出了一个新的想法,或许是由他之前关于相变的研究工作推导出来的。他在信中说:“这些方程的解具有比这些方程本身更低的对称性,”但是“这与其说是一个理论不如说是一项工程。这项工程是宏伟壮阔的,但它仍然需要努力去做。我相信这将会是理论物理学的主要任务。”⑨
海森伯随后响应了朗道的建议,进一步研究了真空态的概念,而真空态的性质正是蕴藏于一个场理论的概念结构下面的。海森伯首先在ResearchontheNon-linearSpinorTheorywithIndefiniteMetricinHilbertSpace[4]一文中借助简并的真空态来解释内部的量子数,后来又在ZueTheorieDerElementarteilchen[5]一文中断言:“理论是否会给出一个具有原方程所有对称性的真空态绝不是先验地确定的”,而且正因为如此“它并不应该被认为真的是真空,而是一个世界态,它形成了基本粒子赖以存在的基底。所以这个态必然是简并的”,而且“是对称性破缺的基础”[6]。海森伯关于简并的真空态的想法是影响深远的,但是他从未达到对对称性破缺的起源、机制和物理后果的令人满意的理解,也没有给出对称性破缺的令人信服的数学形式。
海森伯的想法在场论中的实现最早是由南部阳一郎[7]、南部和Jona-Lasinio[8]提出的。他们把BCS——Bogoliubov的超导模型——应用在具有手征不变性的场理论中,并将前者中以声子为媒介的相互作用替换为费米子之间的非线性相互作用。在Bogoliugov的模型中,基本的激发态是赝粒子或者双双带电的库珀对,它们的能量间隙解释了超导现象。带电对的量子态并不是电荷的本征态,所以它不是规范不变的。所以真空态作为这些库珀对的冷凝物也不是规范不变的,因此是简并的。南部研究的一个重要结果是顶点部分方程的一个精确解,即导致Ward恒等式,并因而保证了整个理论规范不变的赝粒子的集团模式,是有着零自旋和零能量-动量的一个粒子对的束缚态。所以当真空态简并的时候,无质量无自旋的束缚态的存在看起来就是规范不变性的逻辑结果。南部将这套理由移植到一个手征不变的理论上,并在些许改变的基础上把恢复对称性的集团模式解释为介子,也就是相互束缚的核子-反核子对;这样就成功地解释了PCAC——比如Goldberg-Treiman关系——成功的原因。
南部的工作实际上已经否证了一个广为接受的误名:自发的对称性破缺。对称性总是被一些物理机制破坏的,比如超导体中库珀对的形成,或者南部自己的非线性费米子相互作用,但从来都不是自发破坏的。是某种动力学机制将系统从能量的对称状态带入到不对称状态的。对称性破缺的动力学起源⑩也可以在戈德斯通的研究中清晰地看到。
戈德斯通对海森伯关于简并的真空态呈现的对称性破缺的想法,探索的理论语境与南部非常不同。南部是在一个自相互作用费米场的不可重正化模型中,对真空的本性和无质量无自旋的束缚态不可避免的出现考察了对称性破缺解的后果,而戈德斯通则是在一个自相互作用玻色场的可重正化模型中考察一种场论具有对称性破缺解的条件。南部和戈德斯通都观察到恢复对称性的无质量玻色子在对称性破缺的场论中必然的存在。但与南部的费米子-反费米子束缚对相反,戈德斯通的玻色子产生于一个第一性的标量场;在南部的情况中手征对称性是被费米场的未知自相互作用破坏的。而在玻色场的自耦合之外,戈德斯通还发现,只有当玻色子的质量平方为负且耦合常数满足某个不等式时,他考察的场模型才有一个对称性破缺解,也就是说,场会具有一个简并的真空,包含着由超选择规则分隔开的无穷多个最低能态。
戈德斯通模型的一个创新点在于他引入了与“更根本的”费米场毫无关系的第一性的标量场。看起来戈德斯通走出的这一步是随意的或者说至多是探索对称性破缺相关问题的特设性方式,因此这被Leonard Susskind和其他一些人视作“一个严重的瑕疵”。学者们已经投入了很大的精力去摆脱这个根本的标量场,可是所有的努力都已经宣告失败。在根本的标量场这个理念被提出的半个世纪以来,它已经在场理论模型的对称性破缺的探索中成为了一个新的组织原理。
戈德斯通的研究中影响最深远的结果就是他如下的观察:每当原本的拉氏量有一个连续的对称性的时候,任何的对称性破缺解都会被一种必要但不存在的无质量玻色子所否定,这就是所谓的戈德斯通玻色子。这个观察对于所有后续对对称性破缺的探索来说都是具有革命性的第一步,并且很快就经过向一般情况的推广进而成为一个定理,即戈德斯通定理[9]。这个定理对规范理论的对称性破缺解的探索提出了巨大的挑战,因而敦促着热心于对称性破缺的人们把对它的祛除提上日程。尽管在数学上这种祛除是不可能的,在随后的发展中这个定理本身却变得几乎毫无影响。这个定理的证明中关键的一点就是洛伦兹不变性的假设。但是在规范理论的语境中,一种洛伦兹不变的公式化是包含着非物理的自由度的,比如有着负概率的类时的规范玻色子。由于这个原因,在这个语境中所有关于这一问题的有意义的讨论都必须用库伦规范(或者后来在EW理论的语境中的幺正规范Unitary Gauge),这就在没有明确洛伦兹不变性的情况下清楚地展现了这个理论中实验可测的粒子的清单。这一步的合理性被认为是脱离了原定理的假设。但事实上这也揭示了原定理的无关性,尽管这种无关性对很多人来说并不是立刻就很清晰的,即使现在也不是。但无论如何,戈德斯通原本对恢复对称性的无质量玻色子的观察仍然是有效的,而且必须得到妥善的处理。
这项工作有着足够的可能性,因为在那时已经有了另一个由施温格提出的与这个问题相关的创新体系[10]。在规范理论中有一个对称性破缺解的一个理论动机就是要利用有质量的规范玻色子去解释短程的核力。施温格是从动力学的视角来研究这个问题的,并没有明确地提及对称性破缺,因为他相信“对规范不变性的一般性要求看上去不再像是驳倒了这个核心的动力学问题”[10]。
施温格在一个2维无质量量子电动力学的简略模型中证明,当规范场与一个对称流之间有强耦合时,如果规范场的真空极化张量在类光动量处具有一个极点,它可能就不是无质量的。这里设定的场-流耦合表明,这个规范玻色子被考察的语境是一个相互作用理论而不是一个纯粹的规范理论,不是那种流中包含另一个场,并且流和规范场的相互作用在有些条件下可以促成极点出现的规范理论。尽管对称性破缺的理念并没有被施温格采用,但不管是联系于一个场(基本场或是复合场)与规范场相互作用的非零真空期望值的极点本身,还是它给予光子质量的结果,都和对称性破缺有着紧密的联系。施温格没有特意指出真空极化张量中出现一个极点的原因,他只是断言极点的产生是动力学的,与通过南部的束缚态的方式极为相似。但是它的标量特性使它可以容纳“它产生于一个基本的标量场”的解释。Englert和Brout很快就把握住了这个解释上的灵活性[2],而他们在这方面的研究成果所导致的机制正是本文的主要内容。
施温格的模型是平庸的,但他的洞见为许多追随者建立了一个宏伟的理论框架。菲利普·安德森[11]是第一个追随者,他用等离子激元这个案例来证实施温格的洞见:南部的无质量集团模式或者束缚态通过和电磁场的相互作用被转换为一个有质量的等离子激元。从这个案例出发,安德森表示“给规范场赋予质量的唯一的机制就是简并的真空这一类的理论”。他甚至说:“戈德斯通零质量问题没有那么严重,因为我们很可能能够用一个同样的杨-米尔斯零质量问题把它抵消掉。”
在思想上,安德森是第一个将施温格的机制同对称性破缺和戈德斯通玻色子联系起来的人。不过在物理上,他提出的这个联系却是非常薄弱的。他关于等离子激元的非相对论的例子,确实在对称性破缺和施温格使规范玻色子通过与另一个场相互作用而获得质量的策略之间建立了某种联系;但在他的例子中对称性破缺的物理机制来源于南部的束缚态而不是戈德斯通的基本标量场,在那时基本标量场的概念在粒子物理学中是不可行的,甚至现在也不行,正如我们在注释⑨中看到的一样,而且这一点也在TheCaseoftheCompositeHiggs:TheModelasa‘RosettaStone’inContemporaryHigh-EnergyPhysics[12]一文中由Arianna Borrelli仔细地考察过。
在具体的物理层面而不是模糊的思想层面上,使戈德斯通的标量系统适用于施温格的宏伟框架中的第一次努力是由Englert和Brout做出的[2]。在他们关于标量量子电动力学的模型(这可以被延伸为非阿贝尔对称性而不涉及重大的结构性变化)中破坏对称性的标量系统是耦合于规范场的,而在这个模型中,他们直接将规范场真空极化圈最低阶摄动计算中恢复对称性的无质量玻色子解读为施温格极点的物理基础,这可以理解为同有质量的规范玻色子的存在相容的一个数学表达。这个解读可以被看作安德森假说的实现。但在理解戈德斯通玻色子和规范系统(规范系统包含着标量系统的潜在对称性,而因此是与它耦合的)的共生性质这个层面上,这个解读应该被当作物理学中的一个真正的突破。带有对称性破缺解的标量系统和纯粹的规范系统都不能单独存在,而不经过被包含却不存在的无质量(标量或矢量)玻色子的否定;它们只有作为一个共生体的两个不可分离的矩才能存在。
他们关于共生体特性的理解中的一个缺陷就是错误地声称:“对称性是通过规范场自己发生破缺的”。实际上,对称性主要是被标量矩的自相互作用打破的,尽管这个打破的过程可以通过标量场的规范耦合传递到规范系统中去。但这个理解要求我们事先充分理解希格斯最初的工作[3],下面我们就来讨论这个问题。
三、EBH机制的概念基础
希格斯在SpontaneousSymmetryBreakdounwithoutMasslessBosons[3]一文中极富科学创造性地提出了“诱导的对称性破坏(Induced Symmetry Breakdown,缩写为ISB)”的新主张,这个主张一经提出,概念上的情况就立刻变得清晰起来。希格斯认为,当一个带有破缺对称性的标量系统汤川耦合到一个不含有额外的对称性破缺机制的旋量系统的时候,标量系统的对称性破缺会打破旋量系统的对称性,破坏的程度取决于汤川耦合常数,而因此这就允许系统具有有质量费米子的非对称态,这个质量也是与汤川耦合常数成正比的。Englert和Brout的构想很完美地适用于希格斯的主张:他们提到的规范耦合与希格斯理论中的汤川耦合起着同样的作用,也就是说,标量系统的对称性破缺都是通过这样的耦合传递到矢量系统的。所以在矢量和旋量系统中,由有质量的矢量粒子和玻色子展现出来的对称性破缺与它们自己的简并真空态并没有关系,而是由标量系统的主对称性破缺分别通过规范耦合和汤川耦合诱导而来的。
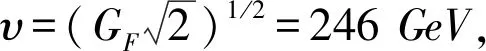
所以EBH机制可以很恰当地被简单理解为分别以耦合常数λ、g和η为特征的标量场的一类耦合:它的自耦合导致了它自身的对称性破缺解,它的规范耦合和汤川耦合导致了规范场和旋量场的对称性破缺解,表现为有质量的规范玻色子和有质量的费米子,就像上文中指出的那样。

四、实在论与工具主义的对垒
尽管我们有上一节提到的结论,EBH机制的意义却仍然受到关于它的基础的看起来比较幼稚的问题的些许烦扰:标量场的对称性破缺解在物理世界(而不仅仅在数学公式中)存在吗?普通的观点会毫不犹豫地说:它当然存在,它的无质量模式与无质量的规范玻色子相结合(“被无质量的玻色子吸收”),导致了我们想要的有质量的规范玻色子,因为由这样的玻色子所产生的实验现象早已全部毫无疑问地被确证了。至于它的有质量模式,尽管在很长一段时间里一直难以寻觅,现在它终于还是在CERN的大型强子对撞机被实验观察到了。既然它存在的所有后果都已被确证,人们可能会感觉它的存在就被确证了。并且这似乎也意味着建立在它上面的EBH机制也被确证了,就像普通的观点声称的那样。一个迂腐的人可能会认为通过确证后果来说明前提的有效性是一个逻辑谬误。然而确证后果至少已经为前提提供了证据上的支持。不过在这个案例中,相比于来自归纳逻辑不完全有效性(即局部辩护)的问题,还有来自物理的更加严重的问题困扰着我们。
前文提到的普通观点的有效性明确地或是隐含地建立在两个假设的基础上。第一,一个标量场的对称性破缺解和规范场的对称解,至少在一个较深的层次上,一个可能无法被现在、未来、甚至是思想上的实验所触及的所谓形而上学(本体论)的层次上,都存在于现实中。第二,在实验的(“物理的”)层次上,它们中的一部分总是会以一种重新定义的(重新组合的)方式作为有质量的标量和矢量玻色子出现。也就是说,无质量的标量模式和无质量的矢量模式都被当做真实的,但不是以一种相分离的方式在观察上、实验上、经验上可触及的。
可是,如果单纯地没有任何实验方法,甚至没有思想实验,来验证它们可分辨的存在,特别是验证从可分辨的戈德斯通模式能够推导出来的效果——要么直接通过戈德斯通模式的导出耦合来验证,要么间接通过分离由该模式从有质量规范玻色子作为媒介的事件产生的效果来验证,那么相信它们存在的立足点是什么呢?一个工具主义者可能会在这里否认标量场的对称性破缺解和规范场的对称解的实在性,把它们降格到燃素和以太所处的虚构地位,认为它们唯一的功能就是构建可观察的粒子(有质量的规范玻色子和希格斯玻色子)和可测量的参数(弱尺度和质量,它们的比就是相应的耦合常数),这在实证主义-工具主义的哲学看来就是物理世界仅有的实在性。也就是说,工具主义者不会认为温伯格模型比格拉肖模型多了什么东西[14],除了一个额外的希格斯玻色子之外。
(一)实在论者的回应:将标量-矢量共生体作为新的基本实体
没有经验的(包括虚拟经验,也就是通过思想实验)方式可以分别验证标量场的对称性破缺解和规范场的对称解,这为工具主义者“EBH机制的物理基础没有实在性”的论断提供了很强的支持,因此也对实在论者对EBH机制的解读提出了严肃的挑战。
不过实在论的解读仍然是可能的,只要我们放弃普通观点所采纳的假设,转而假设现实中存在的东西是对它的标量和矢量的矩具有对称性破缺解的标量-矢量共生体,而不是标量场和矢量场的一个集合。或许EBH机制的物理基础正是这个本体论第一性的共生体——它的内部动力学解释了EBH机制——而不是我们在第3节所讨论的第一性的标量场和它的一些耦合。
这个共生体作为物理上基本的实体和经验上可触及的不可分解的单独实体,在数学上可以被解析地可分离的结构(标量区和矢量区作为共生体的两个矩)来描述,但是任何数学上的分离和操作都不会有任何物理意义,因为它的矩在物理上是不可分的。也就是说,它的标量矩的对称性破缺解或者矢量矩的对称解的无质量激发态都不应被认为在现实(物理世界)中可以探测到:这些激发态只是不可分解的结构在数学上不合法分解的人造产物而已。共生体的整体论结构与其他的一些结构是非常不同的,比如电子-光子耦合系统的结构,这个结构的组分(电子和光子)在无规范极限中可以单独存在,而且它的组分不可能以不同的方式重组而产生不同结构的分量场系统的配置。一个古老的基督教格言适用于这样的整体论共生体:上帝已然结合起来的东西,人们就不要拆散它。
关于本体论第一性并且作为整体存在的、物理上不可分离的两个矩的共生体的假设并不与它的两个矩在动力学上可分辨的假设相矛盾,而实际上前者是必须由后者来补充的。也就是说,每个矩都有它自己的动力学的个体性,即它与其他系统之间不受另一个矩的耦合方式所影响的独特的耦合方式。这意味着标量矩的每一个自由度共享着这个矩独特的自耦合和与费米系统的汤川耦合,而不受矢量矩的规范耦合的影响;相似地,矢量矩有着与其他系统规范耦合的独特方式,这种方式同样不受标量矩的耦合方式的影响。
这个假设对基于共生体的EBH机制的实在论解读至关重要,因为没有这个假设的话,在一个深刻的、实验无法触及的现实层次上,标量矩的自耦合和汤川耦合(标量系统的对称性破缺解和相关的简并真空态,以及由前者诱导的费米系统的对称性破缺解和在此被构建的相关的有质量的玻色子)都不能被定义;并且在实验可触及的现实层次上,矢量矩的规范耦合(以及电弱相互作用)也都不能被定义。也就是说,没有这个假设,我们就根本没有办法去定义共生体内的两个截然不同的矩;这样一来,标量-矢量共生体这一概念本身就会坍塌,而以共生体的概念为基础的EBH机制的实在论解读也就随之不复存在了。
(二)与时空的类比:共生体的可重组矩
这样的整体论共生体有着一个广为人知的先驱。在DieGroudgleichungenFurDieElektromagnetischenVorgugeinBewegtenKorper[15]一文中闵科夫斯基宣称:“从此,单独存在的空间和单独存在的时间都面临着消退成为单纯的影子的宿命,而只有二者的一种结合才能保持一个独立的实在性。”相似地,我们可以说戈德斯通的标量系统和格拉肖的规范系统也面临着消退成为单纯的影子的宿命,而除费米系统之外,只有两个(标量和矢量)矩的一种共生体作为一种整体论的实体存在于这个世界的电弱领域内。
进一步分析这个类比可以知道,由于即使在时空是一个独立的实在的情况下,世界的空间方面和时间方面的区别仍然存在,所以类似地我们仍然可以有意义地讨论共生体中以它们的动力学个体性为特征的标量矩和矢量矩——以及它们在实验上可触及的现象(作为共生体内部自由度重组的结果):有质量的标量和矢量玻色子——只要我们理解,它们只是一个单独的物理实体的不同的矩(显现),而并没有物理上的单独的存在性。
标量矩和矢量矩与标量场和矢量场(独立的场或是在耦合的系统中结合起来的场)是不同的,因为这两个矩的共生性质允许它们在共生体中的自由度进行重组。没有这种可重组性,就不能为产生EBH机制的物理设定来定义共生体的内部动力学:由标量矩的非线性动力学(四次自耦合)产生的对称性破缺解将不能通过使规范玻色子有质量来诱导在矢量(规范)矩中的对称性破缺,因为这只能通过重组共生体中的自由度来做到。
(三)共生体的实在论不同于场的实在论
如果共生体在电弱世界中是一个第一性的实体,那么观测到希格斯玻色子(或W玻色子和Z玻色子)就不能被当做标量场(或规范场)的激发态的确证,就像旧实在论的本体论会主张的那样。与此相对的观点是,这种观测只能被当做共生体的标量(或矢量)矩的激发态的确证。这两种实在论立场的区别有着重大的科学意义。旧观点把最近对希格斯玻色子的观测当做标量场的实在性的确证,这在物理上有着一整套的后果,因为这会吸引人们用这个新的观测结果去解决基础物理学中的未解之谜,例如暴胀子(inflaton)和暗能量。
然而,共生体的观点就会把对希格斯玻色子的观测当做对共生体的标量矩的确证。也就是说,我们把有质量的玻色子当做共生体标量矩的量子激发态,这个激发态在它与物理世界电弱领域的其他量子激发态相互作用时可以被观察所记录,但它在物理上与共生体的其它激发态是紧密联系在一起的,包括那些规范玻色子。所以无论希格斯玻色子的后果指向哪里,共生体存在的一整套后果,包括但不限于W玻色子和Z玻色子的影响,也应该同样得到认真的考虑。“上帝已然结合起来的东西,人们就不要拆散它。”这会严重地制约对这些后果的探索,但它也会为这些探索提供巨大的预测力。
(四)两个谜题
使得矩可重新定义(作为相关自由度的重新结合)的自由度可重组性(来自共生体中不可分割的矩)是共生体的一个特有的性质。这对于为产生EBH机制的物理设定而在共生体内定义内部动力学来说是至关重要的(正如我们在4.2节的结尾所讨论的那样),因此对EBH机制的实在论基础来说也是至关重要的。然而当我们带着应有的谨慎去审视这个主张时,一些令人烦恼的特性就会浮现,而且共生体这个概念本身(进而包括EBH机制的实在论解读)也会遭受严重的威胁。
温伯格在他提出场的重新定义(通过来自标量场和矢量场的自由度的重新结合,正如规范玻色子的重新定义中发生的过程一样)这个关键概念的经典论文AModelofLeptons[13]中指出,这种重新定义意味着微扰论的重新排序。这两者(重新定义和重新排序)如何联系起来的细节可能是解决这里研究的微妙概念问题(来自共生体两个矩的自由度的重新结合)的一个有效技术手段。温伯格当然只假定了基本的标量和矢量场,而不是第一性的共生体。但是我们下面要考察的关于重新结合的概念问题在这两种语境下都是一样的。温伯格没有详细说清那些技术细节,但在两种语境下我们似乎都有理由假定,为重新定义那些场(或者说矩,按我们的说法)而要被重新结合以及在微扰论中要被重新排序的东西的个体性应当在这些过程的前后得到保持;不然的话,如果我们不能明确提出相关的物理过程或物理机制去解释它们的个体性怎样变化,无法控制的概念混乱就会接踵而至。
对于自由度的个体性而言,它的一个重要的方面就是动力学的个体性(这对定义矩来说是至关重要的,正如我们在4.1节讨论的那样),即它与其他系统耦合的独特方式。因此,一个标量自由度有着和它自己(自耦合)以及和费米子(汤川耦合)耦合的特征方式。一个自由度的动力学个体性应该在重组过程中得到保持的合理假设意味着——用更加物理的语言来说就是——一个矩的自由度同其他(包括它自己)物理系统的耦合(例如标量场的自耦合或汤川耦合)的本质必须保持原样,无论这些自由度在何种重构过程(共生体中的自由度重组)下转移到什么组织当中。
通过重组或重新定义,温伯格注意到:“戈德斯通玻色子(在温伯格那里就是标量场的无质量模式,在讨论共生体的语境下就是标量矩的无质量模式)不具有物理的耦合。”他所说的“物理的耦合”意思当然是实验可触及的耦合,而不是它在实验不可触及的层次上与其他物理自由度的所有动力学相互作用。标量场(或矩)的无质量模式在场(或矩)的重新定义的过程中并不出现;它们只是被重组到矢量场(或矩)当中,成为它们的纵向组成部分。因此他们的动力学能力(在它们与其他物理自由度的耦合中显现出来)并不消失,只是以不同的形式得到重现而已。事实上,标量场(或矩)的无质量模式与其他物理自由度的动力学相互作用可以很容易地被理解为通过规范玻色子与其他自由度的动力学相互作用得以实现,表现为它们的纵向组成部分。于是似乎没有什么东西通过重新定义而神秘地消失。
但这里确实有个谜,只不过是另一个类型的谜:关于标量场(或矩)的无质量模式的耦合特性的转变问题。在它们同标量场(或矩)的另一个模式、希格斯模式和费米子的相互作用中,它们原本的自耦合和汤川耦合通过重组被转变为规范耦合,这使它们成为有质量的玻色子的纵向组成部分。
物理学家还没有着手处理甚至还没有注意到这个问题。考虑这个问题的最接近的途径——尽管不是直接去解决它——是由温伯格在他的经典论文发表的将近20年之后才提出来的[16]。在他的著作《量子场论(第二卷:现代应用)》的第21.1节,温伯格证明在无规范极限中,对于一般的物理过程“规范玻色子交换矩阵元的过程(描述的是以同粒子流进行规范耦合的规范玻色子为媒介的物理过程,这在他的书中表示为方程(21.1.22))和戈德斯通玻色子交换矩阵元的过程(描述的是以带有同粒子流的标量玻色子耦合的戈德斯通玻色子为媒介的不同的物理过程,这在他的书中表示为方程(21.1.24))是同样的。”来自不同耦合(一个是标量耦合,另一个是矢量-规范耦合)的相同数学结果可能已经暗示着二者之间的密切联系,但这并不是通过对同一个自由度的重新定位从一种耦合转向另一种耦合的充分的解释。从温伯格的数学操作中无法看清这种转变的物理机制究竟是什么。
如果我们想要把EBH机制当作实在的机制来看待,而不是仅仅把它当作获得格拉肖模型所需经验参数的非实在的工具,那么这个谜就必须被解开。然而现在这仍未得到解决。
与此相关的、或者说更加深刻的问题是:来自标量-矢量共生体的两个矩的那些自由度借以重组,进而导致相关的场(或矩)得以重新定义的物理媒介或者过程是什么?在时空这个共生体的类比中,它的空间和时间方面的重组是由两个参考系之间的相对速度来驱动的,所以这个重组是灵活而多变的,取决于相关的可变的速度,并且这可以导致空间和时间方面的多种不同的配置。那么我们的标量-矢量共生体(或者就此而言的温伯格的体系)的重组也存在类似的灵活性和多样性吗?如果是这样,那么支撑这样的灵活性的物理基础是什么呢?迄今为止这样的基础从未被探索过,并且除了来自原本的拉氏量的那些自由度固定地“重组”为有质量的规范玻色子和希格斯玻色子之外,实际上在相关文献中也没有任何灵活性和多样性的痕迹显现出来。如果这种固定性不能被消解,那么这个共生体就只能作为一种心理上帮助理解的手段,而且基于共生体的EBH机制也会被迫成为获得可观察粒子和可测量参数的特设性手段,而因此不能再被当作实在的东西。
五、结论:不确定性依然存在
如果标量场的对称性破缺解和规范场的对称解的不可测量迫使我们放弃建立在标量-矢量场系统这个基础上的EBH机制的希望,转而构想一个本体论上第一性的整体论标量-矢量共生体作为EBH机制的可能的基础物理实体;如果共生体的每个矩的动力学个体性——它对于定义这个矩的特征耦合(或者甚至是定义这个矩本身)是至关重要的,以及共生体的可重组性——它使得定义共生体内部动力学进而为EBH机制提供物理设定成为可能,都是这个共生体的特征性质;那么解决4.4节所讨论的耦合转变问题和矩重组的固定性问题就是为EBH机制建立一个实在论解释的必要条件。
在耦合转变问题和矩重组的固定性问题得到解决之前,EBH机制的不确定状态——究竟是亚原子范围内基于物理上真实的共生体的物理实在,还是非实在的在心理上帮助理解的特设性手段——没有因为有质量玻色子被观测到而发生任何改变。

为了给“EBH机制对我们理解质量的来源有所贡献”这个论断提供正当的理由,首先必须证明这个机制本身是真实的。但这个问题仍然有待解决。基于这个原因,EBH机制只能被当作一项未完成的工作。
致谢
本文第2节、第3节和4.1-4.3节的早期版本曾发表在由Ettore Majorana基金会和Ettore Majorana科学文化中心资助的,于2013年6月24日-7月3日在意大利埃里切举办的第51届国际亚原子物理学会(关于大型强子对撞机下一步策略的思考);非常感谢彼得·希格斯、Alan Walker、Frank Close以及其他与会专家提出的问题和评论。同时我由衷地感谢Stephen Adler、James Bjorken、Heinrich Leutwyler、John Stachel和Sam Schweber与我讨论,以及他们给予我的评论、建议和帮助。(本文经作者授权译自Cao T Y. The Englert-Brout-Higgs Mechanism — An Unfinished Project[J].International Journal of Modern Physics A, 2016, 31(35): pp1-20.)
[注释]
① 欧洲核子研究中心新闻办公室:“新的实验结果显示在欧洲核子研究中心发现的粒子是一个希格斯玻色子。”2013年3月14日。
② “2013年诺贝尔物理学奖”Nobelprize.org. Nobel Media AB 2013. Web. http://www.nobelprize.org/nobel prizes/physics/laureates/2013/.
③ 更多关于这个问题的讨论见4.3节。
④ 更多关于这个问题的讨论见第3节。
⑤ 在最近的文献中物理学哲学家和历史学家对EBH机制(或者按照以前的称呼叫希格斯机制)意义的理解非常的混乱:有时让人困惑,有时干脆就是错的。从为了通过研究“规范‘破缺’”来避免“戈德斯通定理的后果”而设计的东西[17],或者由“通过规范不变地转化希格斯拉氏量得到的自由度的单纯重排”推导出来的东西[18],一直到“对这个词的恰当理解是物理系统由对称的相位向不对称的(或破缺的)相位的转变”[19]和“作为自发地破缺的局域对称性的希格斯机制”[20],种种观点莫衷一是。本文的目的并不是为了批评其他的理解,而是为了研究这一机制的本体论基础。所以我仅在接下来的两节阐述我自己的理解,相信读者能够清楚地看到我与其他观点的不同。
⑥ 在这一节和下一节,我试图提供对EBH机制起源的概念发展的各个步骤给出简略但不失准确的描述,并澄清它的基础,其中我也试图对有着相关贡献的物理学家的功绩给出一个公正的评价。至于这一领域更详细的历史研究,请见参考文献[21]和[22]:前者主要聚焦于早期的历史而对这一机制本身的研究来说是很弱的;后者对这个机制本身讨论得非常充分但是它关于戈德斯通定理所扮演的角色的框架概念,进而它对相关工作的判断和对功绩的评价,都是令人怀疑的。本文不会对后者进行明确的批判,但机敏的读者会很容易发现错误地理解戈德斯通定理的角色将会导致的贫瘠的后果,主要是对Guralnik、Hagen和Kibble的贡献不恰当的评价[23]。
⑦ 除非有额外的明确说明,本文的语境严格地限制在粒子物理的范围内。
⑧ 有一位学者要求我为这句话提供一个正当的理由,他问道:“为什么对于海森伯的方法这个层级会成为一个问题?”如果人们注意到“统一场论”这个关键概念,那么其实答案就在这个论断当中,是不言自明的。不过或许说得详细一些对不熟悉这一问题的读者会有所帮助。在海森伯的著作《基本粒子统一场论导引》[24]的第1、3、7、8章中,人们可以清楚地看到海森伯对对称性和对称性破缺的理解深受派斯关于对称性逐级减少的相互作用的层级的观点的影响[25]。在根本上海森伯认为对称性会被相互作用所破坏,而且甚至相互作用的类型都可以用遭到了破坏的对称性的种类来定义(电磁相互作用是以同位旋不变性的违背为特征的;弱相互作用违背了奇夸克数和同位荷的不变性;强相互作用部分地违背了SU3不变性,等等)。所以,在海森伯看来,对称性只能用相互作用来定义。对此最直接的推论就是他的基本场在不同的相互作用中必须显示出不同的对称性破坏。海森伯关于对称性(同位旋等等)的详细想法很快就过时了,但他关于对称性被相互作用破坏的基本想法的核心是正确的。而且,他的想法在历史上也扮演了很重要的角色,这是被朗道关于方程的解具有比方程本身更低的对称性的评论所激发的,从此这成了对称性破缺(它有个约定俗成的误名:自发的对称性破缺)这一观念的经典表述,并且很快在简并真空态的想法中得到新生。作为对称性破缺解的基础的简并真空态的观点(这正如南部和戈德斯通所证明的,是由特殊的理论条件下的特殊相互作用导致的:比如标量场特殊的自耦合)成了随后发展的基础,几乎每一篇重要的论文都引用了海森伯的观点的事实恰恰证明了这一点。
⑨ L. Landau[26]:引用自 L. M. Brown and H. Rechenberg, Preprint MPI-PAE/Pth 42/88(July 1988): 30.
⑩ 一位学者评论道:“(文中)根本没有问到什么可以作为动力学来源,也没问到哪一类动力学可能在对称性破缺的过程中起到作用的问题。”我对此深感不解,因为“哪一类动力学可能在对称性破缺的过程中起到作用”的明确例子是直接给出来的:就是库珀对的形成和非线性费米子相互作用。了解南部工作的读者就一定知道正是这些特殊的动力学机制导致了不对称解,因而它们称得上是对称性破缺的动力学来源。

