基于遗传算法的农业机械调配研究
刘 丽,刘 野,王新利
(黑龙江八一农垦大学 工程学院,黑龙江 大庆 163319)
0 引言
农业机械化程度是衡量现代农业发展水平的重要标志。近年来,现代科技对农业的引领作用加速,我国农机装备水平和农业机械化水平均明显提升。与发达国家相比,我国农业械机化总体水平仍然偏低,地区间发展不平衡、部分地区农机闲置问题非常突出。2016年,黑龙江省农业机械化水平达95%,黑龙江垦区农业机械化率已近100%,且农业装备先进,但由于气候条件限制,这里每年11月至来年的4月近半年的时间大型进口农业机械处于闲置状态。由于农业生产具有较强的时效性和连贯性,对于大范围的农业生产作业,需要对农机资源进行合理配置和有效调度,以按时完成农业生产任务,提高农机利用率,避免农作物损失和农机资源浪费,最终提高农户、机手和农机组织的收益[1]。近年来,黑龙江垦区充分利用农机资源实行跨区作业,大大提高了农机利用率,但如何调配农机以缩短作业时间并降低作业成本,发挥现代大型农机对提高农业生产效率的作用,推进现代农业发展,越来越成为重要的研究课题。
从本质上讲,农业机械调配是一种排列组合的问题,在问题确定时,必定会存在问题的最优解。然而,实际生产中的问题规模往往都比较大,排列组合的可能性呈指数化增长,在人类现有的计算能力下,只能精确求解很小规模的问题,远远不能满足实际的生产需求。退而求其次,学术界提出了启发式算法,这类算法基于直观或经验构造,在可接受的计算资源消耗下,给出待解决组合优化问题实例的一个可行解。虽然该可行解与最优解的偏离程度难以预计,却往往可以在实际的问题中证明可行解的有效性。
作为现代启发式算法的代表之一,遗传算法(Genetic Algorithm,简称GA)是基于适者生存的一种高度并行、随机和自适应的优化算法,通过模拟“染色体”的进化,最终得到最适应环境的个体,即问题的满意解。
1 遗传算法概述
遗传算法[2]是由美国Michigan大学的Holland教授于1975年首先提出的,源于达尔文的进化论、孟德尔的群体遗传学说和魏茨曼的物种选择学说,是一种基于自然选择和基因遗传学原理的随机并行搜索算法和寻求全局最优解而不需要任何初始化信息的高效优化方法[3]。遗传算法将目标问题看作进化环境,将目标问题的解集当作环境中的生物个体,通过适当的编码组合用解来表达个体,解答优劣度代表着个体对生存环境的适应程度,适应度越高,个体存活率越高。算法借此将自然界中的优胜劣汰引入到具体的问题中,采取适当的策略来模拟生物进化中的竞争、繁殖、变异和选择,以引导问题的解逐步逼近最优解。传统优化算法通常以梯度信息接近最优点,容易陷入局部最优而停止搜索;遗传算法则通过全局寻优的方式,提高了找到最优解的可能性。本质上,遗传算法是一种计算机模拟方法,具有适用面广、多点搜索、鲁棒性好、自适应强及并行性高的特点,是一种有着自适应能力的搜索优化方法,在函数优化、图像处理、系统辨识、自动控制、经济预测和工程优化等领域得到了广泛的应用[4]。
2 建立农业机械调配优化问题模型
2.1 农业机械调配优化问题的描述
在确定数目及位置的农机调配站中,派出确定数目的某项单一功能农业机械,完成指定作业区域内的单一目标作业。农机站适合指定作业需求的机型仅有一种;每块农田的待作业面积确定且已知,每辆农机可以依次对多块农田实施作业,且对每块农田都通过一次作业即可完成;农机隶属于特定的调配站,作业完成后必须回到出发站。解答问题需要规划所有农机的作业路线,使得农机在整个作业过程中满足以下优化目标:每块农田都得以被实施作业;整个作业的农机运行路线最短;整个作业过程的时间最短。简而言之,农机调度即是要为所有参与作业的农机选择适当的作业路径,从而生成从各农机站到各农田作业点之间的调度方案,以达到使用最少的农机、最短的作业路径及最短的作业时间来为所有农田实施作业的目标。
2.2 模型假设
1)农机调配站的位置、各农田的位置和面积及农机单日作业能力均确定且已知;
2)一块农田仅由一台农机来实施作业;
3)单台农机的作业能力恰好可以满足单块农田要求;
4)有多个农机调配站,各农机调配站中针对特定农机作业需求只配有一种车型;
5)在一个调度方案中,每辆农机仅仅被分配一次作业路线,该农机从其隶属的农机调配站出发,按指定顺序对路径上的农田依次实施作业之后,返回到其出发的农机调配站;
6)在一个调度方案中,每辆农机至少可以分配到一块农田实施作业任务,即保证所有农机的有效利用;
7)不考虑天气,农村道路阻塞等特殊情况。
2.3 建立数学建模
针对农业机械的作业问题(见图1),按照如下步骤建立数学模型。
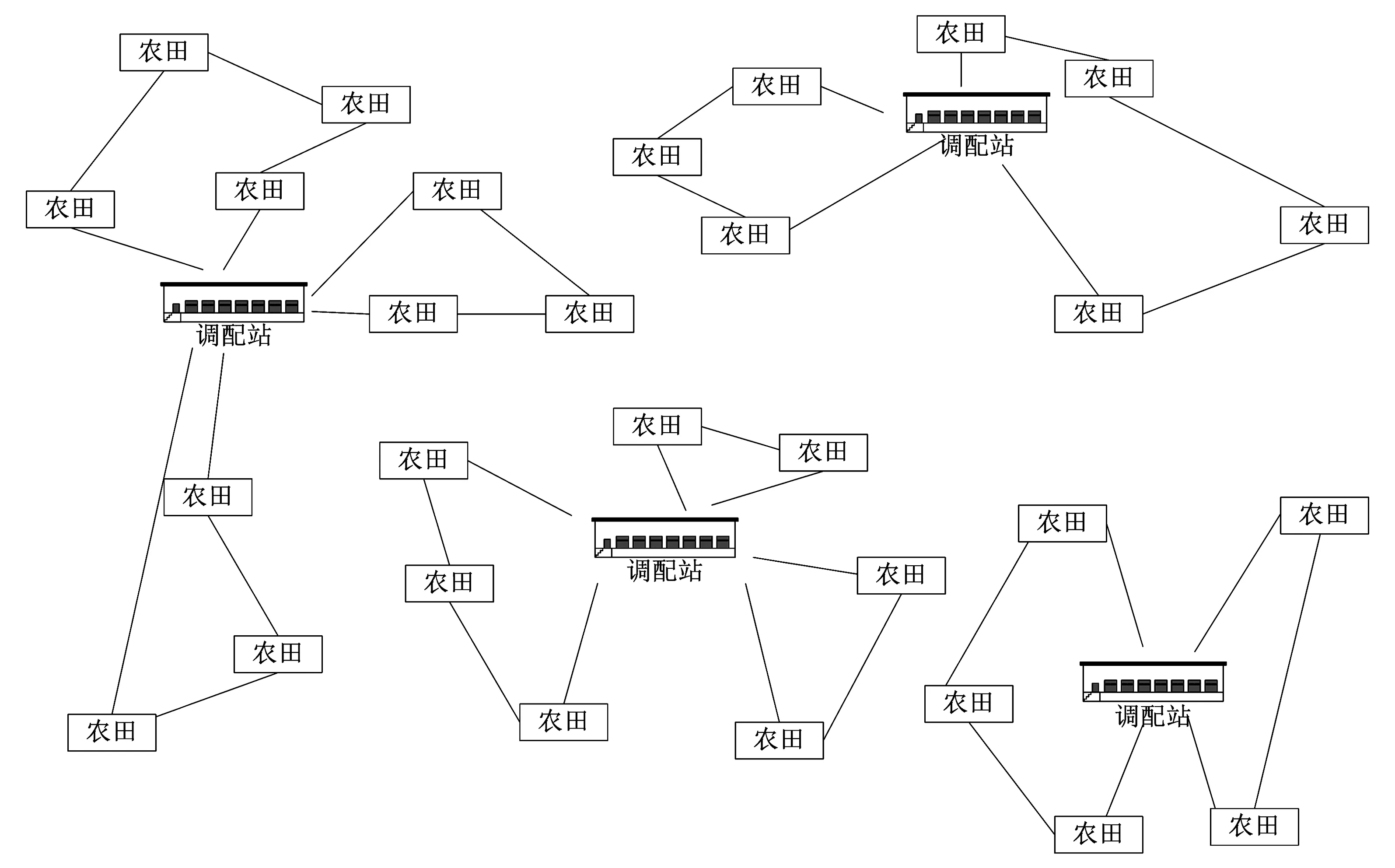
图1 农业机械调配优化路径Fig.1 The mathematical model of path optimization of wheat harvest
1)问题的要素。农机调配站:DP1,DP2,…,DPn,共计n座。可使用的农机:Veh1,Veh2,…,Vehm,共计m辆。
每台农机与调配站的隶属关系:Sub1,Sub2,…, Subm(任一农机必属于某调配站,即Subi∈ DP)。
农田:Frm1,Frm2,…,Frmq,共计q块。为建模及计算方便,农田的划分按农机单日作业量划分,即某块农田Frmi在模型中可由某台机械Vehj单日作业完成。
调配站DPi与农田Frmj之间的路途长度Disij。
农田Frmi与农田Frmj之间的路途长度Dsij。
农机Vehi的作业序列Frma,Frmb,…,Frmp,共计p个(作业序列中的元素为农田,p≤q)。
农田Frmi在作业序列中的顺序[Vehj,Ordk],其中Vehj意为农田Frmi由车辆Vehj作业,Ordk意为农田Frmi在车辆Vehj路径上的序号(任一序列必属于该车辆的作业序列,即Ordk≤p)
2)问题的目标1为所有车辆路径总和最小,由下式表示,即
其中,DS为DS(Sj)(Sj+1),即农机作业序列中相连的两块农田之间的距离;Dis1为Dis(Ci)(S1),即农机所属调配站与农机作业序列中第一块农田之间的距离;Dis2为Dis(Ci)(Sp),即农机所属调配站与农机作业序列中最后一块农田之间的距离。
3)问题的目标2为完成整个作业所用的时间最少,由下式表示,即
min(Ordk)
其中,Ordk即为任一农田在农机作业路径中的序号,所有农田的Ord值最大的一个即为作业全部完成的时间。
4)问题的约束条件1为所有农田都被农机作业,且只由一台农机作业,即
上式表示农田的作业序列中,Vehj为车辆集合V中的任一元素,且该农田在车辆Vehj的作业顺序合法。
5)问题的约束条件2为农机某个作业顺序上,只允许对一块农田作业。
3 农业机械调度遗传算法流程
遗传算法流程如图2所示。
本文所使用遗传算法的计算流程如下:
1)随机产生一组初始个体,形成起始种群;
2)对种群内的每个个体执行适应度判断,保留适应度高的个体,形成新的种群;
3)判断整个算法是否达到了终止条件,如是结束算法,否则进入下一个步骤;
4)对种群执行交叉操作,产生子种群;
5)对子种群进行变异操作,并跳入步骤2)。
4 调度遗传算法设计
使用遗传算法首先要选择合适的染色体编码方式。在问题的建模中,本文使用[Vehj,Ordk]来表示农田Frmi在整个作业序列中由农机Vehj的第Ordk个顺序进行作业。按照这个方式,将所有的农田的作业序列依照农田的顺序依次列出,即形成了一种可能的整体作业方案,如图3所示。
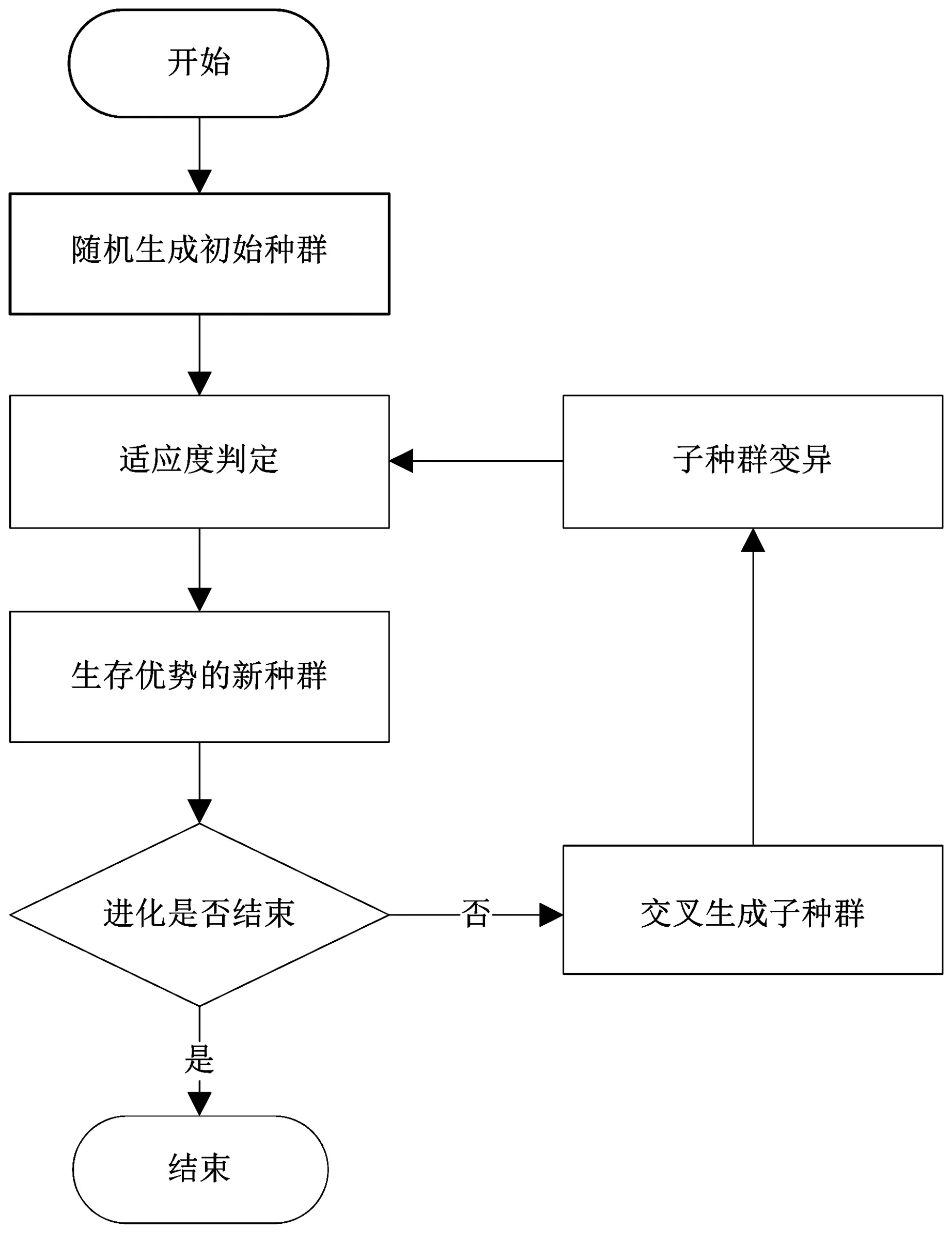
图2 遗传算法流程Fig.2 The genetic algorithm flow
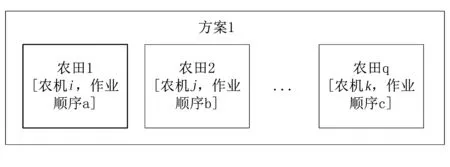
图3 农机作业方案示意Fig.3 The deployment program sketch
图3中,每块农田的作业为一个染色体,所有农田的作业串接成整个方案,形成一个个体。
在构建整个方案的时候,需要满足问题建模时的两个约束条件。
满足约束条件1的方式为:依次为所有农田随机抽取某一台农机作业。
满足约束条件2的方式为:每当抽取到某台农机时,将该农机的作业顺序加1。
1)形成起始种群。为每块农田Frmi随机抽取一台农机Vehj,并将Frmi附加到Vehj现有的作业序列之后。记录Frmi[Vehj,Ordk]为一个染色体。为所有农田抽取农机,形成一个方案,即个体;同时,记录这个个体每台农机的作业顺序。重复这个过程Par1次(Par1值可由问题的规模决定,此处设定初始值为10 000),即形成了个体数量为Par1的起始种群。
2)适应度判断。适应度(Fit)直白地表达了个体的好坏。在问题建模时有两个目标:总路径最短(Fitdis)及作业时间最短(Fittim)。将两个目标按照Par2及1-Par2的比例加权作为适应度来判断个体的好坏,即
Fit=Par2·Fitdis+(1-Par2)·Fittim
Par2的值初始假定为50%,即认为总路径最短和作业时间最短的重要性相当。可以调节Par2的值来加强某一目标的权重,如天气状况不良,抢收时的作业方案计算,就应当将作业时间最短这个目标的权重加强(如Par2=10%)。
计算总路径最短的适应度Fitdis,首先要计算每个个体各自的总路径TtlDs,计算方式为累加每台农机的行驶总路程,即
因为路径短的个体适应度应该更高,将每个个体的总路径TtlDs取倒数,然后按照个体与总体的比例计算路径适应度,即
计算作业时间最短的适应度Fittim,首先要计算每个个体各自的作业时间,计算方式为选取作业序列最长的农机的最后一个序列号为该个体的作业时间,用Ordmax表示。
因为作业时间段的个体适应度应更高,将每个个体的作业时间Ordmax取倒数,然后按照个体与总体的比例计算作业时间适应度,即
将整个群体中的每个个体的适应度都计算出来后,按照适应度由高到低排序,保留前10%的个体作为新的种群,种群规模变为了0.1Par1。
3)算法终止判断。算法以固定的迭代次数Par3作为终止条件,迭代次数达到Par3则终止计算,将适应度最高的个体作为解决方案输出。
4)交叉形成子种群。由2)中形成的0.1Par1规模的种群为父种群,按照轮盘赌的方式执行交叉策略,生成子种群,子种群的规模恢复为Par1大小,如图4所示。具体的策略如下:首先从父种群中随机选择两个个体,方式为在区间(0, 1]上随机两次,得到两个随机数;父种群是按照适应度从高到低依次排列的,且所有个体的适应度和为1,两个随机数落到哪个个体的区间,则这两个个体成为双亲。
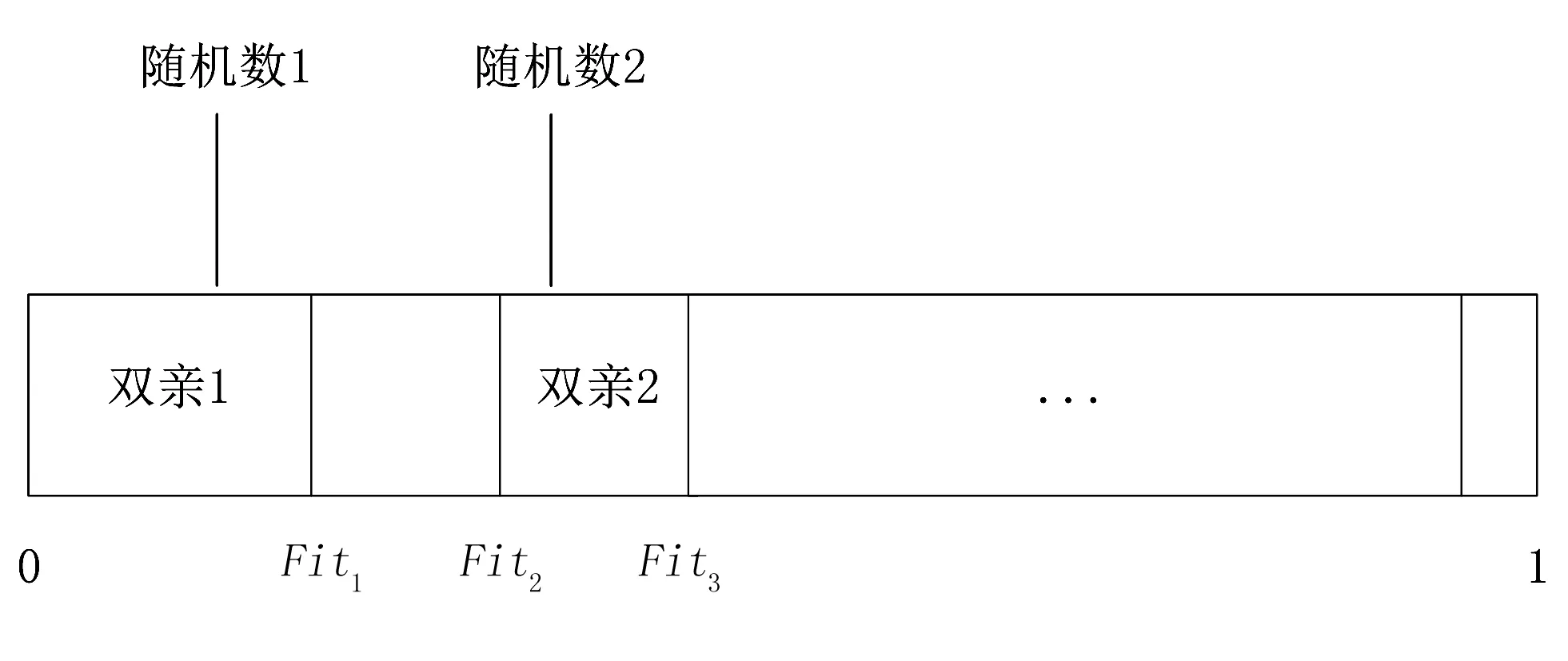
图4 双亲选择示意图Fig.4 The parents choice sketch
选中双亲以后,由双亲交换多个染色体生成两个子代,如图5所示。策略为:随机选择多个染色体Frmrdm,进行互换。
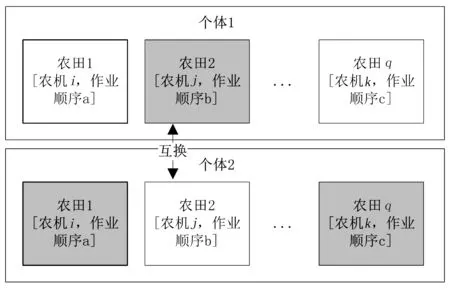
图5 染色体交换示意图Fig.5 The chromosome exchange sketch
图5中,双亲交换了染色体2,形成了2个新的子代,交叉完成后,需要对每个子代的新的染色体执行合法化。将原来的染色体[Vehold,Ordold]删除,将农机Vehold的第Ordold作业序列删除,并将后续作业序列前提;然后添加新的交换来的染色体[Vehnew,Ordnew],将农机Vehnew的第Ordnew作业序列之后插入农田Frmrdm,并将后续作业顺序后延。在合法化的过程中,非Frmrdm的染色体也会随之发生更新。
重复选择双亲生成子代的过程0.5Par1次,子代种群达到Par1规模。
5)子种群的变异。以一个较低的概率Par4(初始设定为0.1%)随机选择子种群中的个体,对选中的个体随机挑选多个染色体Frmrdm,随机更改该染色体的农机,作业顺序则保持不变。个体变异以后也需要执行合法化。方式与4)中相同,不再赘述。
5 农业机械调度遗传算法的应用与分析
使用MatLab编程本文设计的算法,并以随机生成的数据(4个站点,40台农机,400块农田)为例进行计算,如图6所示。

图6 遗传算法算例Fig.6 The genetic algorithm example
初始种群Par1设定为2 000;两个目标的比例加权Par2设定为50%;迭代次数Par3设定为10 000次;变异比例Par4设定为0.1%。
计算完成后,可看到各台机械被分配到的农田数量均匀,作业路径合理,路径交叉路线较少。证明算法的设计是合理有效的,结果如图7所示。
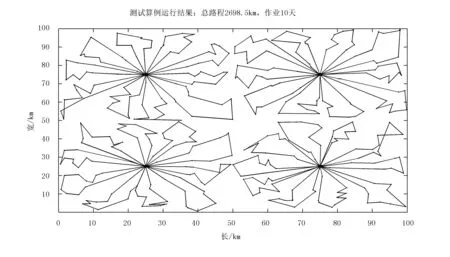
图7 算法结果Fig.7 The genetic algorithm result
作为对比,假设一种由人工指定作业的方式:所有车辆负责等面积的作业区域,作业路径按维度依次排列,这种方式与现实世界中的人工调配比较相似。最后的作业结果如图8所示。
对比使用遗传算法的结算,路程由2 698.5km增加到3 592.2km,作业天数由10天增加到12天。遗传算法的运算结果明显优于简单的按区域划分分配作业车辆的方式。
遗传算法本质上是一种规则约束下的全局搜索,随着问题的复杂化,解空间的大小对比算法计算量趋向于无穷大。所以,算法难以保证最终解与最优解的接近程度。遗传算法解的演进方式为:先探索,再验证,接受或否定本次探索,算法特性决定了它的搜索方向是随机跳动的。这样做的益处在于保证了搜索的全局性,但对特定解的局部优化则不是算法的优先考虑项。反映到实际的运算结果中,往往发现可以对结果进行局部微调优化,这种微调既可以人工进行,也可以另设计算法处理。图9为对遗传算法运行结果进行人工微调后的示例。
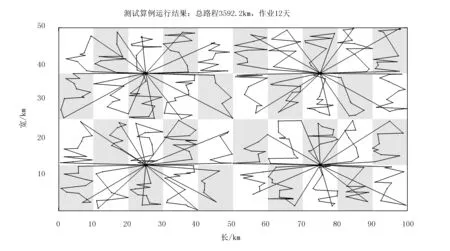
图8 人工调配结果Fig.8 The manual deployment result
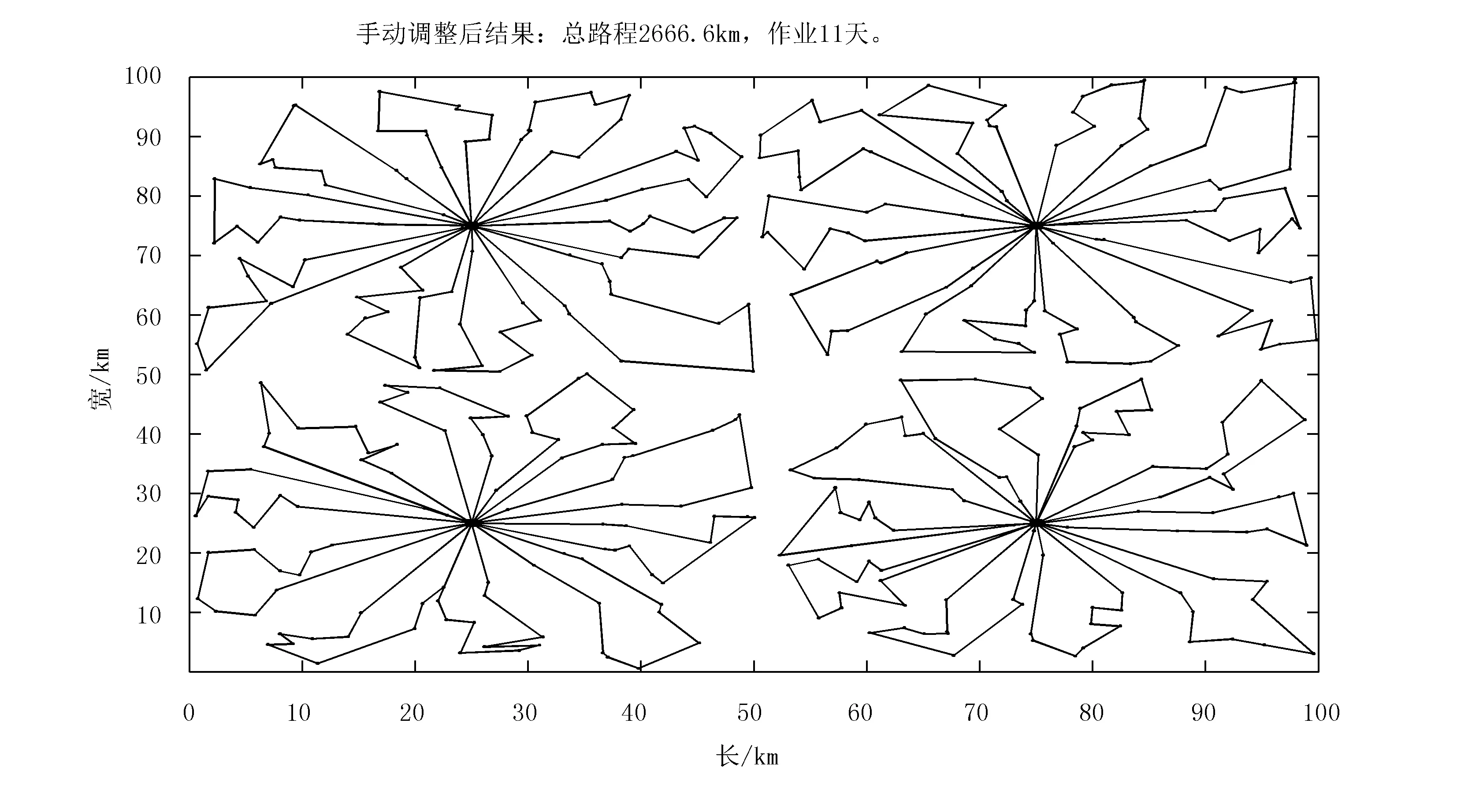
图9 人工微调结果Fig.9 The manual trimming result
由图9可以看出:手动微调以后,总路程稍微下降至2 666.6km,作业天数增加到11天。人工微调的作用比较有限,而如果设计算法进行局部微调的话,则可能会有更明显的优化效果,从而形成遗传算法搜索全局、微调算法局部优化的结构。因本文重点不在于此,故不展开研究。
为测试遗传算法计算结果的稳定性,重复执行算法,计算20次,各次结果分布如图10所示。
由图10可见:各次结果离散性较小,算法求解效果稳定,具有较高的实用性。
6 结论
对农机调配问题进行建模,使用遗传算法进行编程及算例运行,证明遗传算法适用于解答较大规模的农机调配问题。本文所构建的遗传算法使用比较简单,运行结果稳定,输出的调配方案整体优于人工调配方案,可明显缩短农机调配的作业里程及工期,具有较高的实用性。同时,也应看到因为智能算法固有的特性,算法运行结果并不能保证为问题最优解,对结果进行特定方向的人工再调整在实践中仍有其必要性。
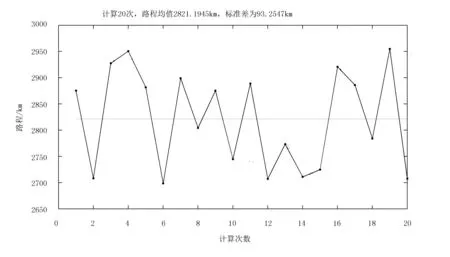
图10 结果稳定性Fig.10 The results stability

