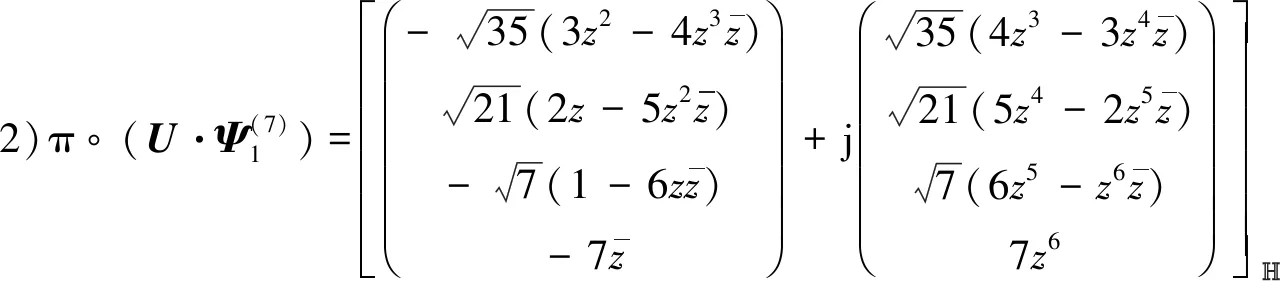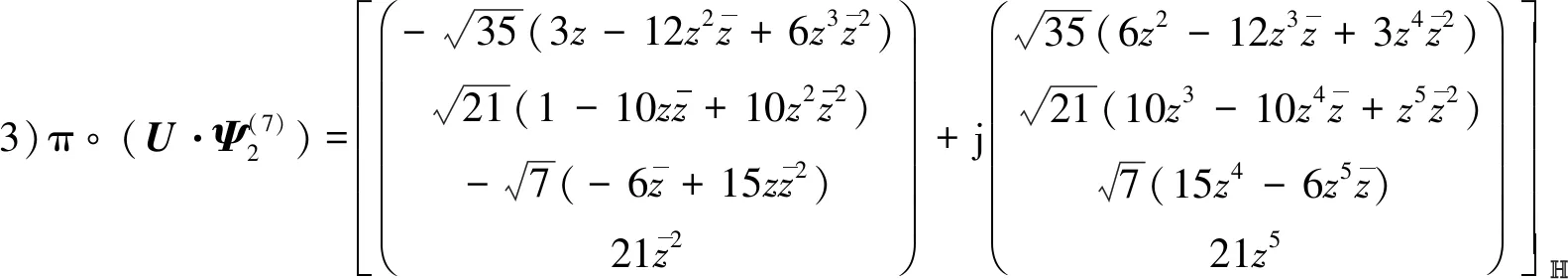HP3中共形极小曲面的几何*

高紫娟，焦晓祥

(中国科学院大学数学科学学院, 北京 100049)

对极小曲面的研究一直是微分几何研究领域中的一个重要课题,特别是关于极小曲面的几何性质以及分类问题的研究。当外围空间是空间形式的时候,一些重要的分类结果已经先后被提出。更为一般的情况是外围空间是对称空间的时候,对称空间中的极小曲面研究也有不错的进展,但依旧有许多值得关注的问题。所以,本文主要关注外围空间是四元素射影空间的情形,这对于四元素射影空间中极小曲面的几何及分类的研究是具有重要意义的。

在近几十年中,国内外对极小曲面的研究都取得了许多重要成果。

1982年, Bryant[1]通过扭映射π:CP3→HP1证明CP3中水平全纯曲面的投影为HP1中的极小曲面, 并且构造出CP3中紧致的非分歧的全纯水平曲面。1986年Aithal[2]构造HP2中所有的调和二维球面。 Bolton等[3]也在1988年给出CPn中的Veronese序列即常曲率极小二维球面。1991年, Bahy-El-Dien和Wood[4]构造HPn中的所有的调和二维球面。 2014年,He和Jiao[5]给出HP2中线性满、全非分歧的常曲率共形极小球面的分类。同年,He和Jiao[6]给出HPn中第二基本形式平行的共形极小球面的分类。

近几十年中,关于复射影空间中极小曲面的几何研究, 许多学者已经给出很多重要的结论。 而由扭映射π:CP3→HP1可知四元素射影空间与复射影空间的水平分量有一个自然等同,所以我们希望通过复射影空间研究四元素射影空间。

1 预备知识

首先介绍四元数、扭映射以及相关的一些知识。

四元数H是以1,i,j,k为基的一个四维实向量空间,即H={a+bi+cj+dk|a,b,c,d∈R},其中1,i,j,k满足:

i2=j2=k2=-1,ij=k=-ji,

jk=i=-kj,ki=j=-ik.

由此可见H为一个不可交换环。

因而, 对于h1=a1+b1i+c1j+d1k,h2=a2+b2i+c2j+d2k∈H有

h1h2=(a1a2-b1b2-c1c2-d1d2)+

(a1b2+a2b1+c1d2-c2d1)i+

(a1c2+a2c1+d1b2-d2b1)j+

(a1d2+a2d1+b1c2-b2c1)k.

与复数C类似,四元数上也有个自然的共轭作用*:

若h=a+bi+cj+dk,则h*=a-bi-cj-dk.

更为经常的,我们是把H看成以1,j为基的复数域C上的二维右模,则∀h∈H,可写成h=u+jv,u,v∈C。对于

且知上述两种定义等价。

一般来说, 用Hn表示n个四元数组成的列向量,HPn表示Hn+1中所有通过原点的直线组成的集合,则[h1]H和[h2]H∈HPn,[h1]H=[h2]H当且仅当存在h∈H,使得h1=h2h。

若令Sp(n)={H∈GL(n;H)|H*T·H=In},其中In表示n阶单位矩阵,可在HPn定义一个作用使得HPn有齐性表示

HPn=Sp(n+1)/(Sp(1)×Sp(n)).

根据文献[7]可知有如下的一个交换图：

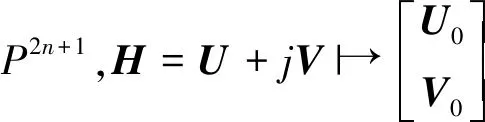
定义1.2扭映射π:CP2n+1→HPn给出CP2n+1的水平切空间与HPn的切空间一个自然等同，所以定义CP2n+1在点[u]的水平部分T[u]为π([u])处纤维的正交补, 其中CP2n+1上的度量为Fubini-Study度量.若Ω:N→CP2n+1称为水平的,Ω的切映射的像落在T[u]中。

T[u]↔{v∈u⊥|σu(v)=0,

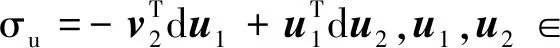
(1)

2 HP3中的共形极小曲面

2.1 HP3中的共形极小曲面

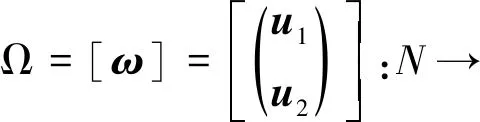
根据Bolton等[3]给出的结论,有如下定义：

例1 通过上述可算得CP7的Veronese序列如下：

对应的Gaussian曲率分别为4/7,4/19,4/27,4/31,4/31,4/27,4/19,4/7。

接下来给出两个引理：

引理2.1[7]对于水平极小曲面Ω=[ω]:N→CP2n+1，则π∘Ω:N→HPn为HPn中的共形极小曲面,其中

π:CP2n+1→HPn为扭映射。

引理2.2[3]设Φ:S2→CPn为线性满的常曲率共形极小浸入,那么在差一个全纯等距意义下,Φ与CPn中的 Vernoese序列可以看作等同。

这样根据上述两个引理，可以得到以下命题。

接下来利用Veronese序列介绍文献[7]给出的构造HPn中常曲率极小二维球面的构造方法。

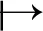
定理2.1设Φ=[ω]=[(ω1,…,ω2n+2)T]:S2→CP2n+1为浸入,若存在U∈U(2n+2)使得U·Φ水平当且仅当

(2)

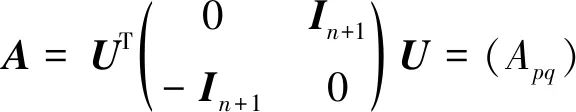
同理，将第2个等式展开,(2)式得证。

2.2 HP3中的共形极小二维球面

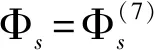
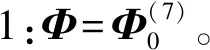
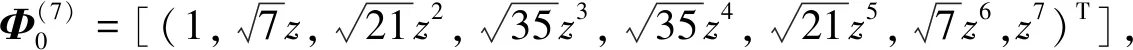
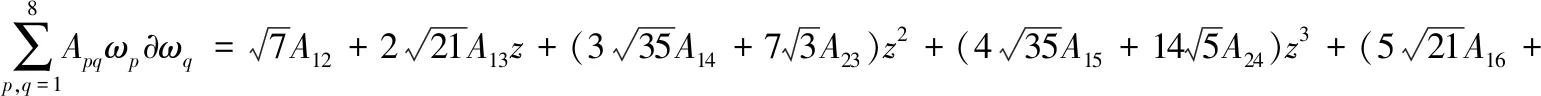
由于A为一个反对称矩阵,所以可算得

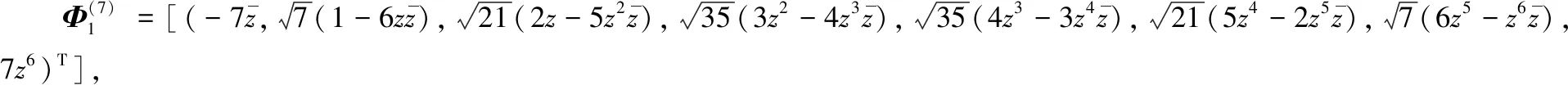
由于A为一个反对称矩阵,所以可算得

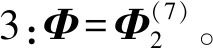
由于A为一个反对称矩阵,所以可算得

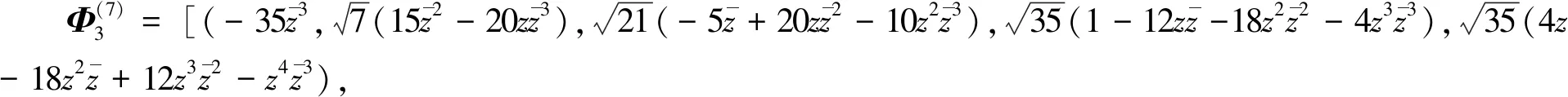
由于A为一个反对称矩阵,所以可算得

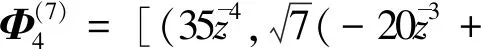
由于A为一个反对称矩阵,所以可算得

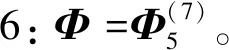
式得

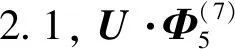
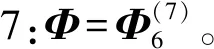
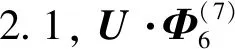
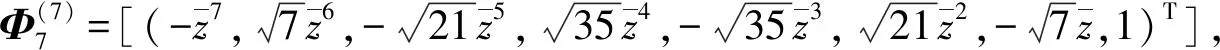
定理2.2设Φ:S2→CP7为CP7中Veronese序列中的一个元素,若存在U∈U(8)使得U·Φ为水平当且仅当U满足

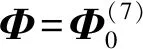
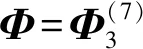
A=0.

接下来,将通过给出上述的解来构造HPn中极小二维球面。

式(1)对应的解

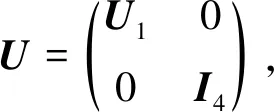
取A26=A37=A17=A28=0,A18=A27=A36=1,所以

为式(1)对应的特解。

此时可算得

式(2)对应的解

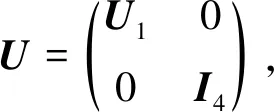
取A17=A28=0,A18=1,A27=-1,所以

为式(2)对应的特解。

此时可算得

式(3)对应的解

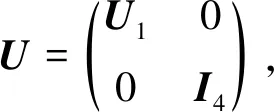
为式(3)对应的特解。

此时可算得

式(4)对应的解

由于A=0非退化,所以此方程无解。

例2 设z为球面上一个全纯坐标,则下述为6个HP3中常曲率共形极小二维球面：