基于SVPWM的变频器死区补偿研究

叶为奇，郑明辉，魏海峰，曾 峰，徐 蔚

(1.江苏科技大学，镇江 212003;2.常熟瑞特电气股份有限公司，常熟 215500)

0 引 言

由于变频器中的功率元件IGBT本身存在导通延时和关断延时(大于导通延时)，为了改变这种情况，在控制脉冲前后加入死区时间。尽管死区时间所占脉冲周期很短，一般只有几微秒，却能够影响变频器电压波形和电机电流波形，不仅提高了其中的谐波含量，而且降低了整个变频系统的效率和性能[1]。在驱动三相异步电机等电机系统中，输出波形含有大量谐波，尤其是幅值较高的低次谐波，本文通过参数对比方法，可以使得输出波形具有电压波形质量高、电流纹波小、直流电压利用率高等优点，通过变频系统最终输出的噪声和振动来加以验证。

目前，关于死区补偿的研究已经有了较大的进展。死区补偿可以从两个方面入手，一方面是通过在硬件电路上增加外部补偿电路进行补偿；另一方面是通过软件算法进行补偿。软件补偿是通过软件程序进行设计，需要高品质的处理芯片，可分为时间补偿和电压补偿[2]。文献[3]通过时间和电压两种补偿方式对正弦和SVPWM逆变器进行改进。文献[4]通过迭代控制策略用旋转变换方式进行补偿。文献[5-6]提出通过在线补偿三相桥臂，对死区时间进行实时同步补偿。文献[7]对满足不同调制程度的补偿方式进行了研究。文献[8]提出了通过扰动观察器对死区时间进行旋转坐标系变换。本文在电流大于零和小于零时只对相应作用触发脉冲进行死区设置，计算相应设定电压空间矢量分量，并验证补偿策略的可行性。仿真对比了输出波形中的不同奇次的谐波含量，实验验证采用死区补偿策略后，电机运行中的振动与噪声都得到了不同程度的下降，对系统的运行起到稳定作用。

1 死区效应分析

在变频器控制IGBT对电机负载进行三相交流输出的过程中，由于功率元件本身存在导通与关断延时，并且在死区时间内整个桥臂上下两部分是不导通的，实际输出电压由续流二极管决定。当所在桥臂上管导通时承受导通压降(I>0)，规定流向负载为正;当所在桥臂下管导通时承受导通压降(I<0)，规定流向负载为负。

图1为三相变频电气图，控制三个桥臂上的功率元件的导通时间来决定输出电压矢量。图2为电流流向示意图，流向电机负载为正电流(i>0)；流出电机负载为负电流(i<0)。

图1 三相变频电气图

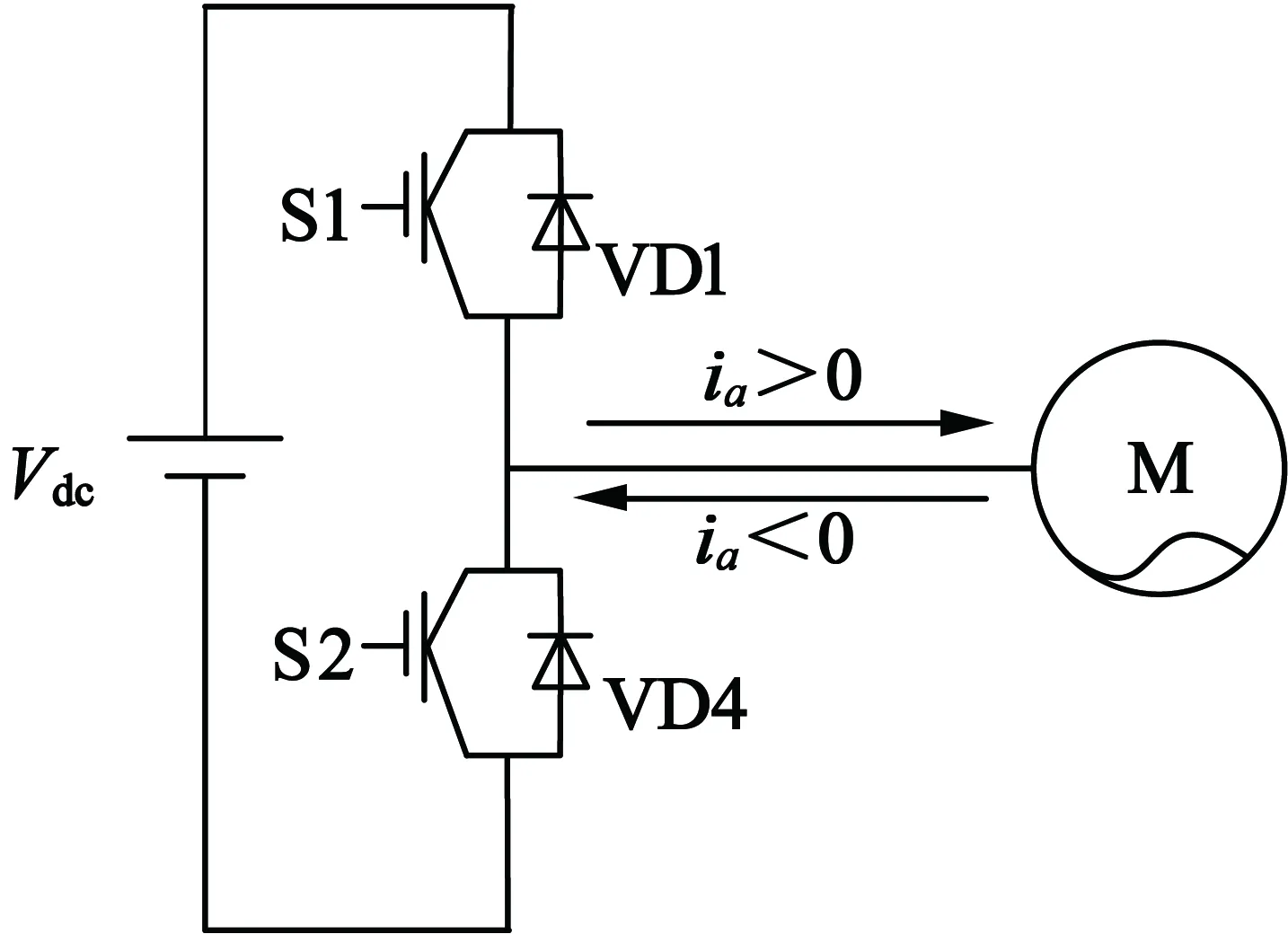
图2 电流流向示意图

图3为A相桥臂波形图。图3(a)为理想脉冲波形图，图3(b)为实际脉冲波形图，由于存在导通和关断的延时，因此脉冲波形有一定的延迟。当IGBT在断开的过程中时，负载端电压是根据续流二极管上的电流流向来决定的，当ia>0时，由于死区时间作用在上升沿，并且脉冲发生是两边对称的，实际输出脉冲宽度比理想的脉冲宽度窄，缩短的时间为(Td+Ton-Toff)/2，如图3(c)所示；当ia<0时，由于死区时间发生在下降沿部

图3 A相桥臂波形图

分，并且脉冲发生存在对称性，输出实际脉冲宽度比理想的脉冲宽度宽，增加的时间为(Td+Ton-Toff)/2，如图3(d)所示。平均畸变电压ΔV可以表示：

(1)

式中：Ts为脉冲发送间隔时间；ton为功率元件的开通延迟时间；toff为功率元件的关断延迟时间。

根据三相电流的极性，三相平均畸变电压分别表示如下：

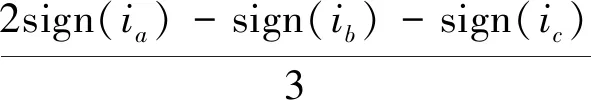
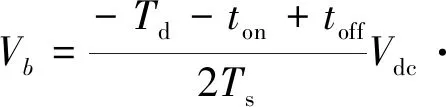
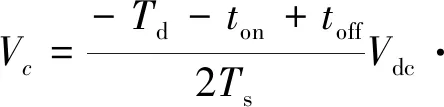
2 死区补偿方案

死区补偿的方案是建立在SVPWM技术基础之上的，先对SVPWM技术进行说明。SVPWM技术控制脉冲的作用时间，使输出电压矢量所形成的圆形旋转磁场符合电机的运转特性，再划分不同的区域(Ⅰ～Ⅵ)，通过坐标变化，将输出电压矢量转变为对应的脉冲作用时间。为了降低功率元件的损耗，相邻桥臂之间的切换，按照100-110-010-011-001-101-100的顺序，进行脉冲调制，实际扇区分布图如图4所示。

图4 空间矢量扇区分布

输出电压矢量Uout在不同时刻所在的扇区也在变化，Ua和Ub分别表示所在扇区的坐标分量，通过矢量运算可以表示为U1和U2的组合。根据U1和U2的作用时间分别表示为T1和T2，作用时间T1和T2可以通过Uout所在扇区的夹角θ来表示，以下列出表达式：

(6)

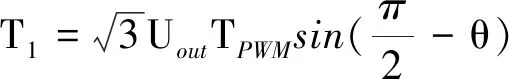
(10)

式中：TPWM为一个PWM周期；Td为死区时间；TE=TPWM-Td。

图5 实际电压矢量分解图

在实现死区补偿电压矢量所在扇区的分解与合成过程中，按照SVPWM技术在第Ⅵ扇区(0～π/3)进行分析论证。图6为第Ⅵ扇区死区时间补偿前后信号图，图6中的阴影区域为死区时间。

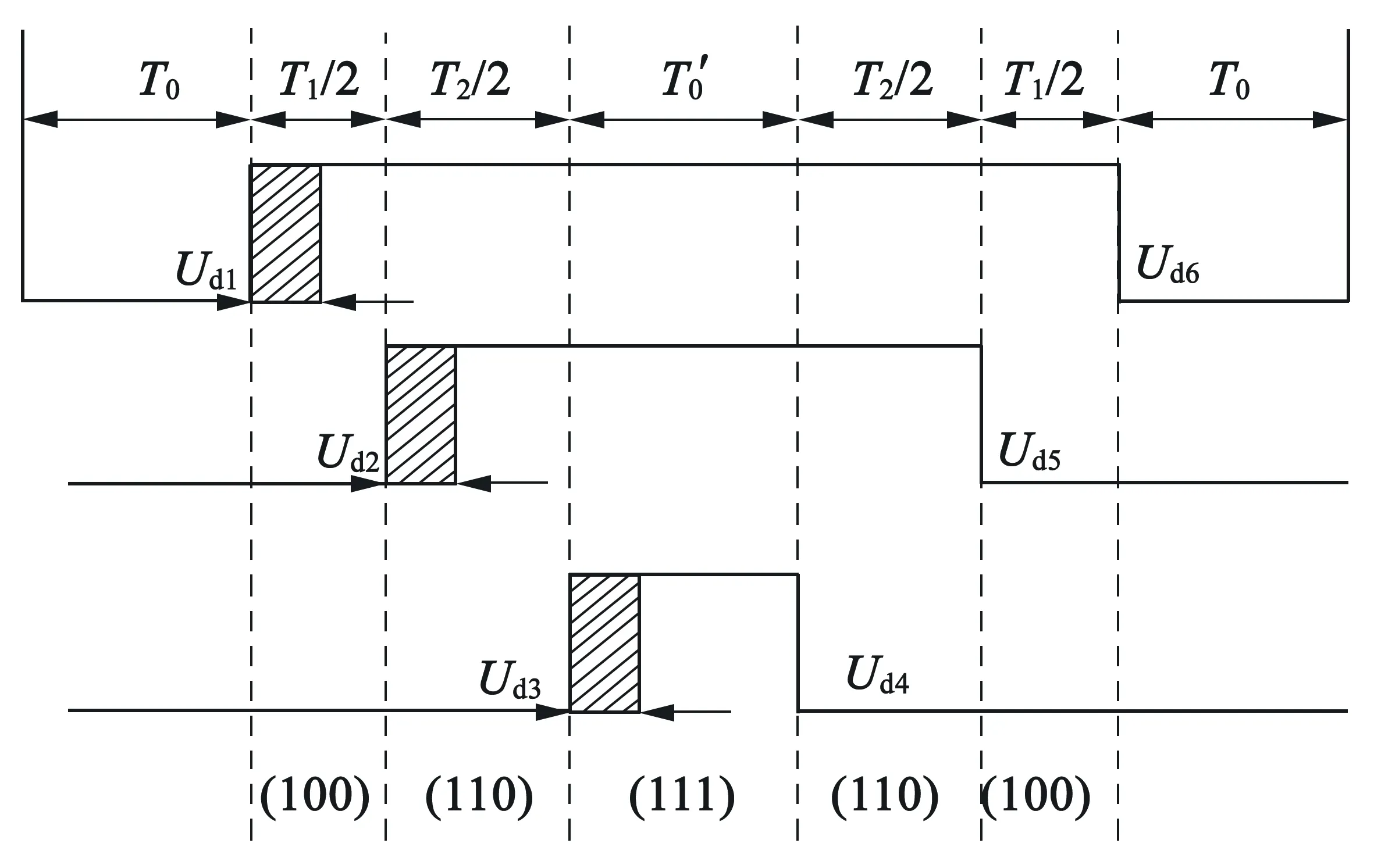
图6 第Ⅵ扇区触发信号图

死区矢量的计算遵循以下几点原则：

(2) 为了减小IGBT开关器件的开关次数带来的损耗，当电流大于零时(i>0)，此时对应的死区时间无作用；当电流小于零(i<0)时，此时对应的死区时间无作用。

如果当前时刻ia>0，ib<0，ic>0，Ud1，Ud2，Ud3处于脉冲序列的上升沿，其中Ud1，Ud3为无效矢量；Ud4，Ud5，Ud6处于脉冲序列的下降沿，其中Ud5为无效矢量。可知，Ud2为(100)，Ud4为(100)，Ud6为(111)。其中，Ud6为零矢量，则在这个周期中：

U=Ud2+Ud4+Ud6(11)

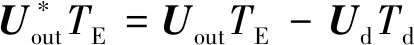
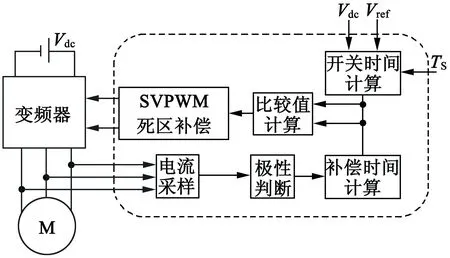
图7 死区补偿原理框图

3 实验仿真

在MATLAB中搭建了整个系统的模型，测量相应的电流电压波形，如图8、图9所示，通过功率分析仪对波形进行相应的谐波含量分析。通过对比可以看出，输出谐波畸变率降低了，输出波形更加圆滑，从仿真角度表明该方法的可行性。

以一台10 kW三相异步电机为实验对象，对实际电机的输出相电流波形以及振动数据进行测量和对比。图10为测试现场图片。图11，图12为实际电机运行中输出端的电流测试波形。

图13为无死区补偿情况的实际电机运行中测得各机脚的振动结果，图14为死区补偿后的电机运行中各机脚的振动结果，结果表明在低频段有明显的降低效果。

图8 无死区补偿的相电流波形及THD

图9 死区补偿后的相电流波形及THD

图10 测试现场

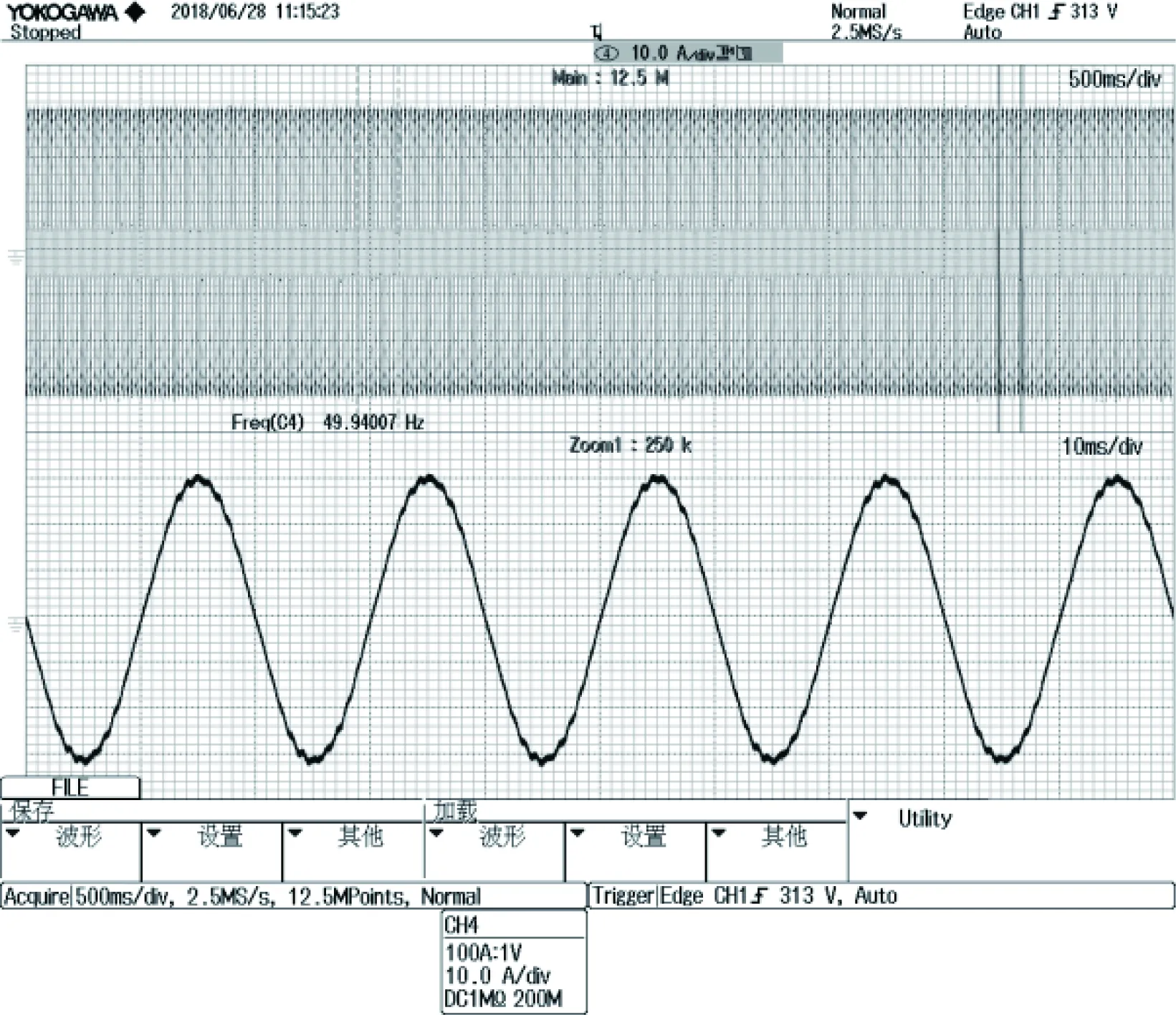
图11 实际输出电流波形

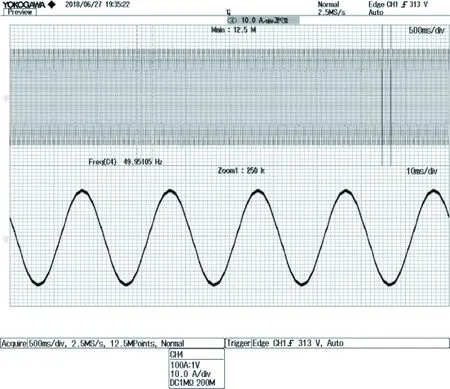
图12 实际输出电流补偿波形

图13 无死区补偿时电机机脚振动

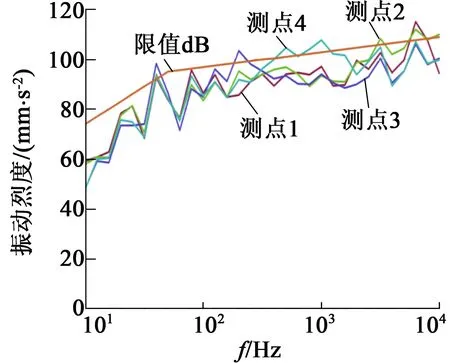
图14 死区补偿后电机机脚振动

图15为无死区补偿情况的实际电机运行中测得噪声的数据，图16为死区补偿后的电机运行中噪声的数据，结果表明在低频段有明显降低噪声的作用。

图15 无死区补偿电机噪声

图16 死区补偿后电机噪声

4 结 语

本文在传统死区补偿的基础上，研究了一种死区补偿矢量合成方法，通过死区补偿矢量和实际合成矢量相转换并建立对应的表格。

以一台10 kW三相异步电机为实验对象，从理论、仿真以及实验三个方面进行研究，并且从最终得到的振动和噪声数据中验证该补偿方法的有效性。