高频脉振电压注入法的转子位置估计误差补偿
陈小玲,唐 鹏,戴跃洪
(电子科技大学,成都 611731)
0 引 言
由于永磁同步电机具有体积小、损耗小、功率密度大、动态性能好、质量轻等优点,在社会的各行各业被广泛应用。传统的永磁同步电机在内部安装有位置传感器。但是,在某些特殊环境中位置传感器的使用反而会使位置检测误差变大,比如,高湿度、超高温、超低温、强腐蚀性、强振动、空气污染严重等严苛环境,进而严重影响整个系统的运行。所以,研究无位置传感器永磁同步电机的控制方法具有重大意义[1]。
目前,常用的无位置传感器永磁同步电机控制方法,根据其速度范围的不同,可以大致分为以下两种:基于基波数学模型的永磁同电机无传感器控制[2]和基于高频注入的永磁同步电机无传感器控制[3-8]。目前基于基波的控制方法一般有模型参考自适应法[9-12]、扩展卡尔曼滤波器算法[13]、滑模观测器法[14-16]、龙伯格观测器法[17]、自抗扰控制算法[18-19]等。但是,当电机处于低速或者静止状态时,电机的反电动势是检测不出来的,所以这种方法适用于中高速段,而在低速段则得不到理想的波形。基于高频信号注入的基本思想是把一个高频的电压信号叠加到电机的固定轴系上,使相应的电流中携带转子的位置信息;然后,通过滤波器提取出相应的信号;最后,经过位置估计器,估计出相应的转子位置。此方法不依赖电机的基波,能在极低速甚至静止状态中估计出转子的位置信息。目前,高频注入法主要包括旋转高频注入法和脉振高频注入法。与旋转高频注入法相比,脉振高频注入法不仅适用于凸极率较大的电机,也适用于表贴式电机[8]。
然而,传统的脉振高频电压注入法在估计转子位置时,忽略了电子电阻以及交叉耦合项的影响,随着转速的升高以及定子电阻的变化,转子位置估计误差会越来越大[20]。本文在传统脉振高频注入法的基础上考虑了定子电阻以及交叉耦合项的影响,通过理论分析,得出了电子电阻及交叉耦合项的影响,不仅存在于转子位置估计式的幅值中,也存在于相位中,而转子位置的信息主要存在于相位中。所以,随着转速的变化,交叉耦合项以及定子电阻能对转子位置估算产生较大的影响。在此结论的基础上,本文提出了相应的补偿措施,并仿真验证了此方法的有效性。
1 理想条件时高频信号激励下的数学模型
利用内置式永磁同步电机明显的凸极,脉振高频注入法在d-q坐标系的d轴持续注入高频正弦电压信号,通过整个系统的处理检测出转子的位置。
内置式永磁同步电机的电压方程:
(1)
式中:ud,uq,id,iq分别是d,q坐标系下的电压和电流分量;Ld,Lq,Rs分别是d,q轴的电感和电阻;ωe为电角速度;ψf为永磁体磁链;p为微分算子。
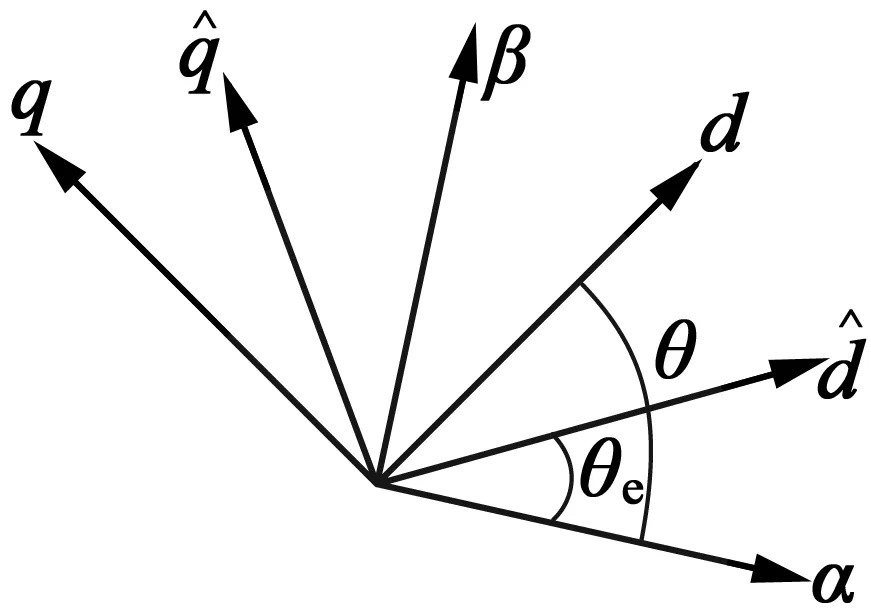
图1 真实坐标与辨识坐标之间的关系
如图1所示,令θe为转子的估计位置角;θ为实际角。那么位置估计误差:
Δθe=θ-θe(2)
根据图1,进行坐标变换,又因为jωhLd/q≫Rs,所以电阻可以忽略:
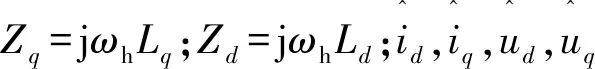
(4)
将式(4)代入式(3)得:
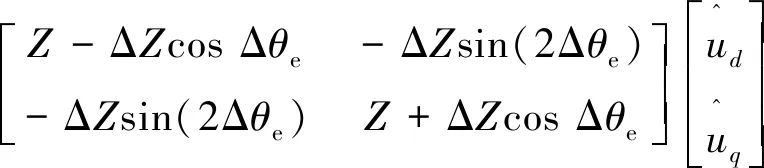
(6)
将式(6)代入式(5)得到高频响应电流表达式:
(7)
式中:ωh为注入高频信号的频率;uin为注入信号的幅值。
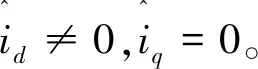

图2位置信息提取
经过提取后,输入PI调节器的表达式如下:
(8)
此关系式忽略了定子电流以及交叉耦合的影响。
2 非理想条件时转子位置误差分析
本文主要讨论定子电阻以及交叉耦合项对转子位子估计的影响。
这里,重写永磁同步电机的电压方程:
(9)
同时考虑定子电阻以及交叉耦合项:
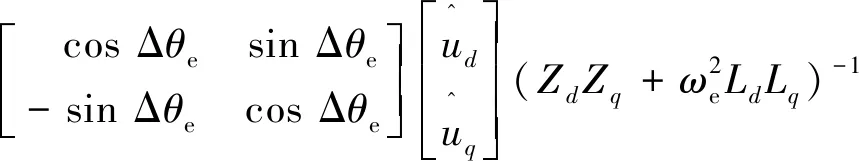
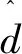
(11)
式中:M1=sin(2Δθe)(Zq-Zd),M2=Ld+Lq+cos(2Δθe)(Ld-Lq)。将分母有理化,得如下关系式:
(12)
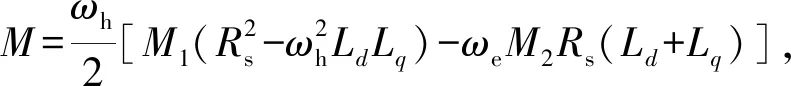
由式(11)可以看出,当同时考虑定子电阻以及交叉耦合时,不仅改变了信号的幅值,还改变了信号的相位。而转子位置误差信号主要存在相位中,其对转子位置信号是有影响的。
位置信号的提取过程同图2,那么输入到PI调节器的信号:
(13)
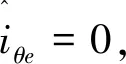
(14)
从式(14)可以看出,转速、定子电阻越大,估计位置角的误差越大,并且,若是两项电感的比值接近1,估计位置角的误差也越大。所以,本文对由定子电阻以及交叉耦合项产生的误差进行补偿。根据有关M的表达式,当估计位置误差足够小时可得:
M′=ωh[Δθe(Lq-Ld)M3-M4ωeLd](15)
那么补偿的关系式:
(16)
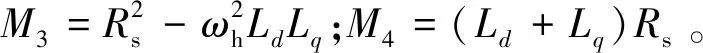
带补偿的位置提取过程如图3所示。

图3 带位置补偿的位置跟踪器
3 仿真验证
在MATLAB/Simulink下进行仿真,参数设置:注入的高频电压幅值为40 V;频率为1 kHz;定子电阻为0.15 Ω;q轴电感为0.520 mH;d轴电感为0.220 mH;磁链为0.017 43 Wb;极对数为4。空载运行时,对补偿前和补偿后的转子位置以及位置误差信号进行对比。
当给定转速为20 r/min时,其结果如图4和图5所示。对比图4、图5可以看出,当电机运行在极低速时,对转子位置估算误差的补偿仍然有效。

(a) 转子位置

(b) 位置误差
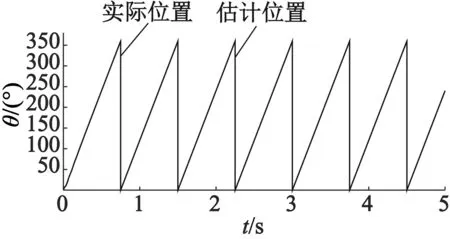
(a) 转子位置
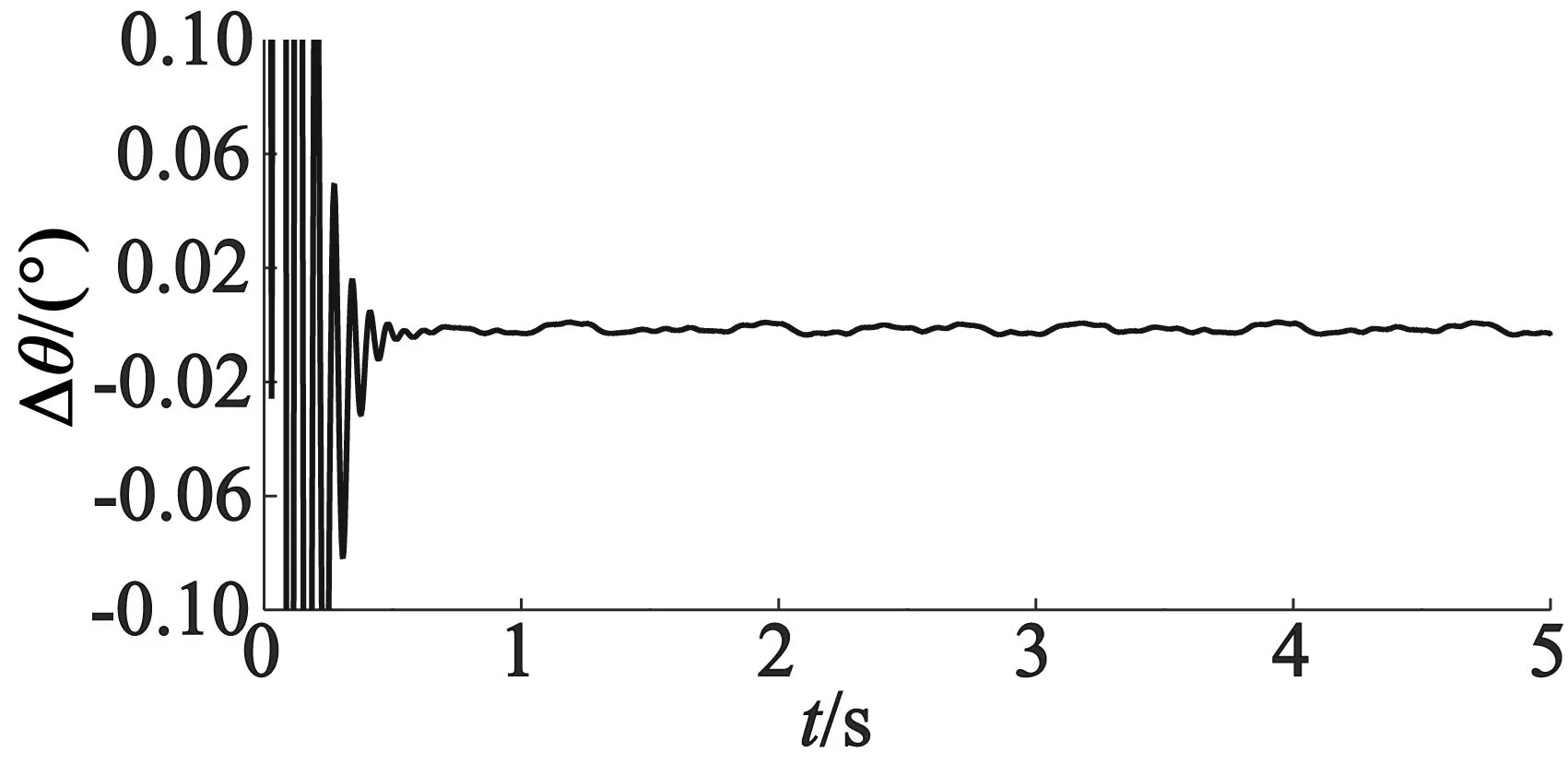
(b) 位置误差
当给定转速为400 r/min时,其结果如图6和图7所示,补偿后转子位置误差明显减小。再对比图4

(a) 转子位置

(b) 位置误差
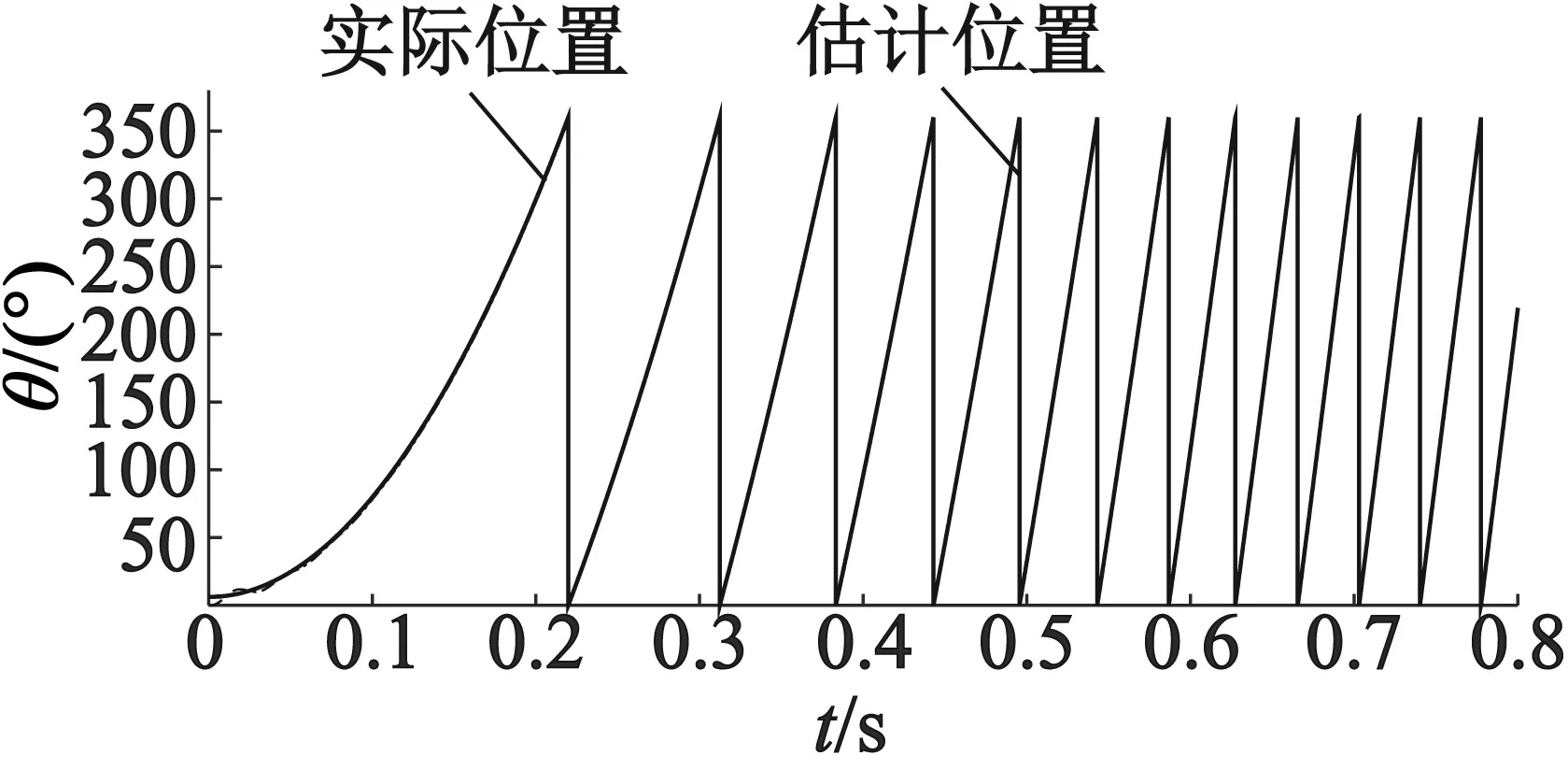
(a) 转子位置
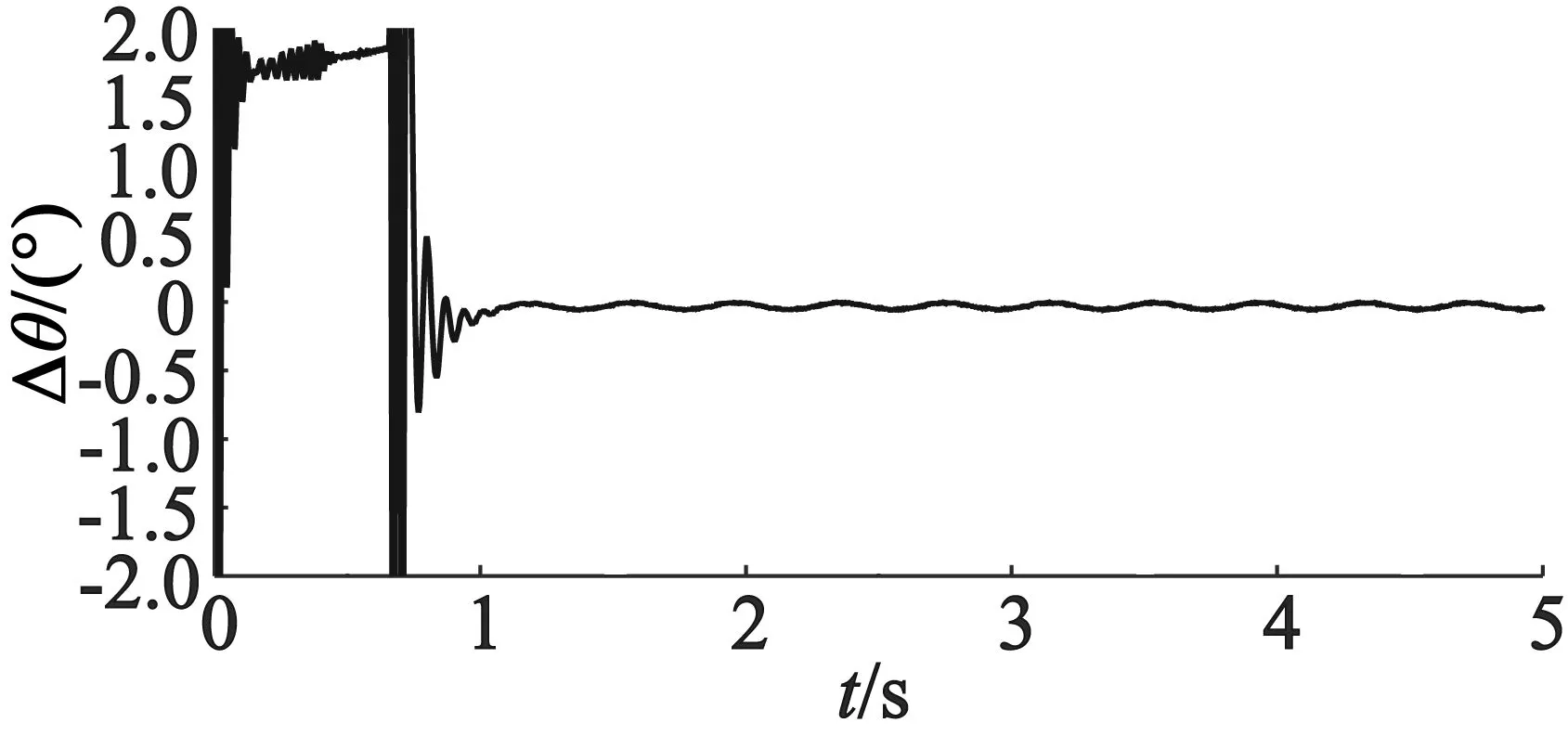
(b) 位置误差
和图6可以看出,随着转速的上升,转子位置估算误差变大,此结果与理论推导出来的结果一致。
进一步增大转速到800 r/min时,其结果如图8和图9所示,转子的位置估算误差进一步增大,经过补偿后,误差有明显的减小。
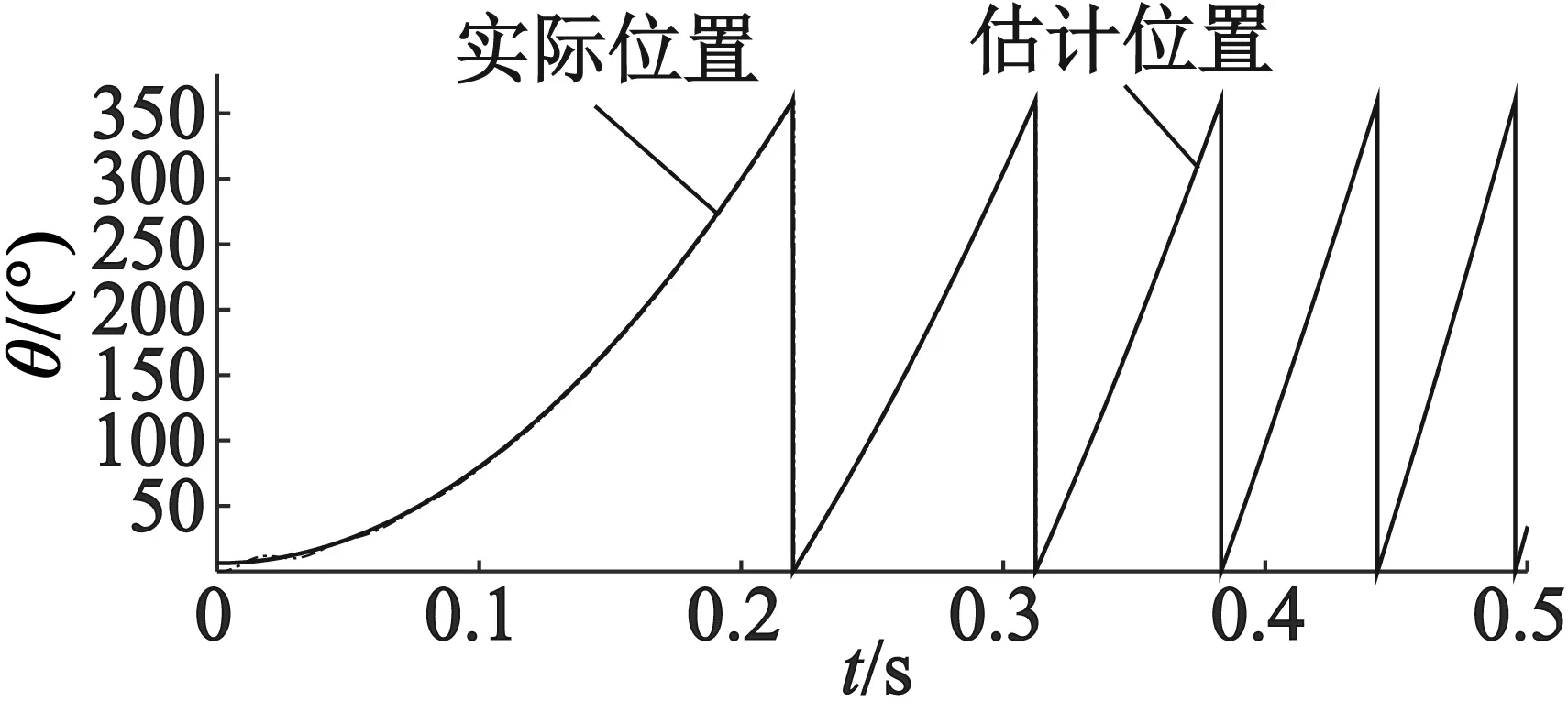
(a) 转子位置

(b) 位置误差

(a) 转子位置
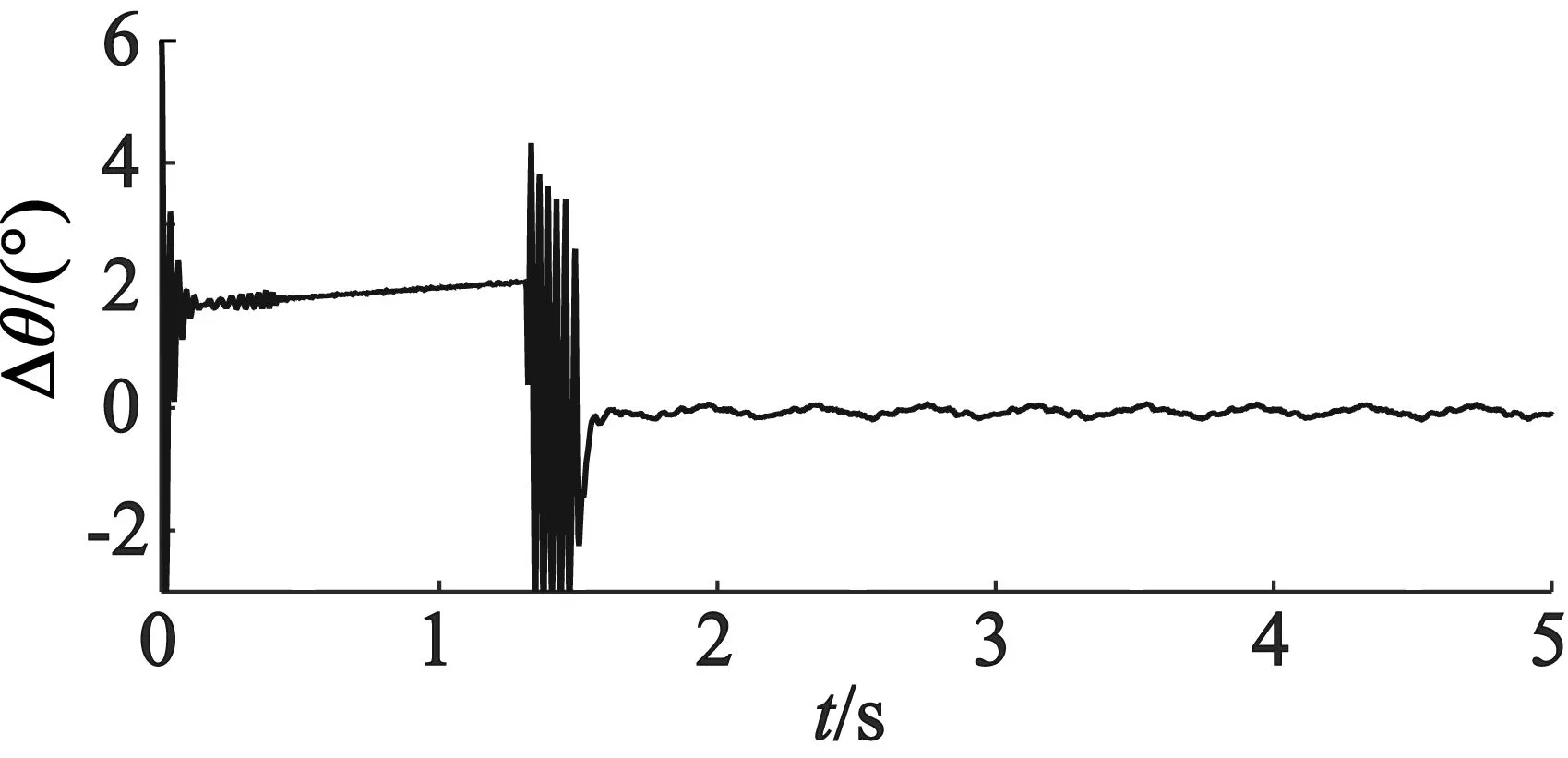
(b) 位置误差
4 结 语
本文通过分析定子电阻和交叉耦合项对转子位置估计的影响,设计了高频脉振电压注入法的转子位置补偿策略,有效地降低了由定子电阻和交叉耦合项导致的转子位置的估计误差。该策略易于理解,实现简单。仿真结果表明了该补偿策略能在中低速条件下有效降低转子位置的估计误差。

