基于ELM实现的IPMSM转矩观测器

厉亚强，张文涛，李涉川

(桂林电子科技大学， 桂林 541004)

0 引 言

内置式永磁同步电机(以下简称IPMSM)由于其功率因数高、起动转矩大、起动时间较短、过载能力强等优点，在机械臂、机器人、电动汽车等领域得到广泛应用[1]。目前，随着电机控制技术、高精度传感器技术以及新型电机控制理论的快速发展，IPMSM控制系统的研究以及应用越来越受到当今电机控制领域研究人员的重视。

IPMSM由于其参数的非线性、波动性和不确定性等原因，准确控制电机转矩具有一定的难度。由于电机工作状态下直接测量真实转矩的成本较高，并且转矩的直接测量受到仪器精度和仪器响应速度的影响比较大，因此通常通过算法来实现对电机转矩的观测[2]。文献[3]提出了一种新型趋近律的永磁同步电机超扭曲滑模直接转矩控制方法，该方法将转矩和磁链作为被控对象，通过引入饱和函数代替传统滞环比较器的方式，使转矩脉动减小了50%；文献[4]提出了一种基于最大转矩电流比的转矩预测控制系统，并对该系统性能进行了相关分析；文献[5]介绍了将观测转矩的前馈补偿融合到控制器中，从而形成了二自由度的控制器，该控制器在响应速度和鲁棒性方面有较好的性能；文献[6]中的控制方案指出了IPMSM在负载转矩波动时，通过引入前馈补偿可以有效地减少转速波动，从而提升控制系统的动态性能。传统的控制方法都存在时效性不高、转矩波动抑制能力差等问题，然而这些问题可由神经网络解决。

近年来，人工智能的核心技术神经网络以其高速的实时处理速度和强大的计算能力获得了广大电机控制学者的青睐，由于不需要准确的电机非线性参数，这使得准确观测电机转矩变得更加容易[7]。文献[8]将RBF(径向基函数)神经网络应用于永磁同步电机PID参数调整中；文献[9]采用了反向传播神经网络(以下简称BP神经网络)对无刷电机进行控制仿真设计；文献[10]采用深度学习方法对永磁同步电机做性能分析。但是深度学习模型如CNN，RNN，LSTM等虽然较普通神经网络有更强的非线性拟合能力，但是其训练优化比较困难，而且在目前的MATLAB版本中无法直接生成可用的Simulink模块，不能实际应用，故本文设计选用能直接实用的神经网络。

基于极限学习机(以下简称ELM)神经网络结构简单、训练快、非线性拟合能力强等优点，本文研究了用ELM神经网络设计的转矩观测器代替数学模型来观测电机转矩，并将所观测的转矩作为前馈补偿，准确控制电机输出转矩的IPMSM转矩控制方法。同时，用实验验证了该结论的正确性。实验结果表明，基于ELM神经网络的电机转矩观测器可以准确观测电机转矩并能较好地抑制转矩波动。

1 控制技术与神经网络

1.1 Clarke变换

Clarke变换是将三相静止坐标系转换为二相静止坐标系的变换，又称3s/2s变换[11]，如图1所示，A,B,C绕组为对称三相绕组，匝数均为NA；α，β轴绕组为正交二相绕组，匝数均为Nα；α轴绕组方向与A相绕组轴线一致。

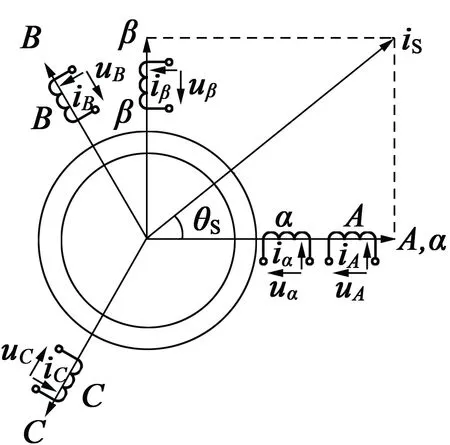
图1 三相静止轴系与二相静止轴系

各绕组通入电流后，只计其基波磁动势，正向电流产生的磁动势方向与绕组轴线一致[11]。磁动势等效是不同轴系之间变换的物理基础和基本原则。因为只有这样，才不会影响电机内机电能量转换。

若三相电流的基波合成磁动势与二相电流产生的基波合成磁动势相等，则有[12]：

(1)

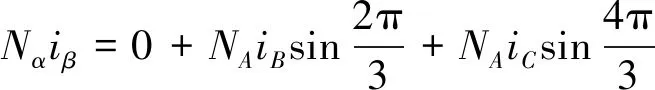
设NA=kNα，则式(1)、式(2)可变换：

(3)

又由于本文使用的IPMSM三相绕组无中性线，即[12]：

i0=k′(iA+iB+iC)=0(5)

(6)

由式(5)可得：

iA+iB+iC=0(7)

代入式(6)得：

(8)

1.2 Park变换

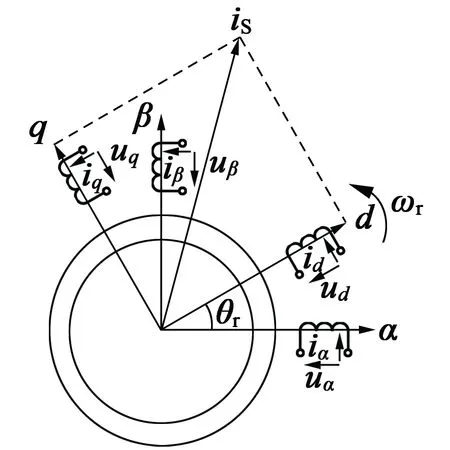
图2 二相静止轴系与二相旋转轴系

Park变换是指两相静止坐标系到二相旋转坐标系的变换，又称2s/2r变换[14]。如图2所示，设静止坐标系与旋转坐标系的相绕组匝数相同，以α轴为空间参数轴，d,q轴系以点角速ωr逆时针方向旋转，空间相位角为θr(电角度)，根据磁动势等效原则，则有[14]：

id=iαcosθr+iβsinθr(9)

iq=-iαsinθr+iβcosθr(10)

可得：

(11)

式(11)即为Park变换表达式，同时能够满足功率不变约束[15]。

1.3 矢量控制的原理

通过Clarke-Park坐标变换，将定子三相电流(iA,iB,iC)变换到两相d,q旋转坐标系下，转换为与转子磁链同向的d轴电流和与d轴电流相位相差90°的q轴电流分量，从而可以用直流电机转矩控制方式来模拟三相交流电机的转矩控制[16]。

1.4 BP神经网络

BP神经网络是一种信号前向传递、误差反向传递的网络。该网络将信号从当前层向下一层传递并直至输出，如果输出未达到设定误差要求，则将输出值与期望值的误差反向传播，并根据预测误差来调整各个神经元的权值和阈值，最终使神经网络的预测输出和期望输出满足设定的误差要求。误差反向传播优化方法一般采用梯度下降法。本文仿真用BP神经网络作为对比实验，其基本框架如图3所示。

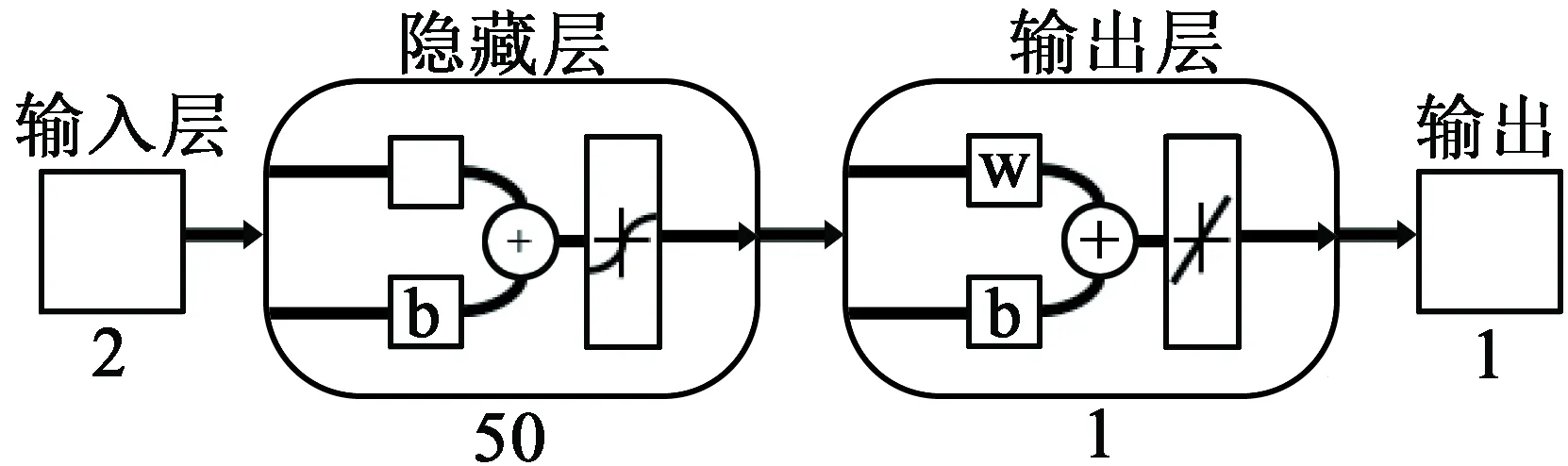
图3 BP神经网络结构

1.5 ELM

ELM神经网络结构如图4所示。

图4 ELM神经网络结构

ELM神经网络不需要提前设置各层神经元之间的连接权值及阈值，仅仅需要人工设置隐藏层神经元节点的个数，并选取一个无限可微的函数作为全部隐藏层神经元的激活函数，便可得到全局最优解。

2 基于ELM神经网络的转矩观测器

2.1 设计思路

本文通过Simulink仿真来模拟电机的运转，并将ELM神经网络封装为一个Simulink模块参与到电机仿真控制中，最后进行简单实验验证。

为了简化电机控制，通过坐标变换将三相电机的三相电压或者三相电流转换到d,q坐标系(即将a,b,c三相电压或者电流变换成d,q轴电压或电流)。在d,q坐标系中，IPMSM的数学模型[17]：

(12)

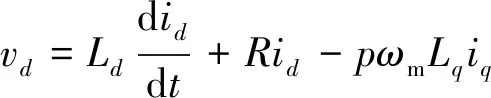
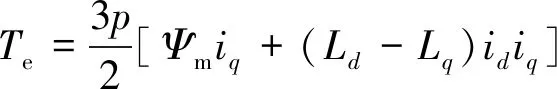
式中：vd，vq为d轴和q轴电压；id，iq为d轴和q轴电流；Ld，Lq为d轴电感和q轴电感；Ψm为永磁体磁链；R为定子绕组电阻；ωm为电机转速；p为电机磁极对数；Te为电机的输出转矩[17]。根据式(12)、式(13)可知，电机d，q轴的电压由d，q轴的电流决定。又根据式(14)可知，电机的输出转矩也由d，q轴电流决定。因此，控制电机等同于控制电机的d，q轴电流。同时根据式(14)可知，id，iq可以有多种组合，产生同样的Te。因此，存在一个id，iq组合的优化值，使得电机效率最高。这可以通过MTPA查表来实现相关的优化效果。

基于上述数学模型，转矩观测器的框图如图5所示。

图5 电机控制框图

2.2 实现方法

图5由ELM神经网络模块，PI转矩控制器模块，PI电流控制器模块，MTPA模块，SVPWM逆变器，IPMSM和解耦装置组成。其中，ELM神经网络模块由MATLAB中训练好的ELM神经网络加一条gensim(net, -1)命令导出。

电机转矩观测器的实现方法：ELM神经网络模块的输入是测量获得d，q轴电流id和iq。将来自ELM神经网络模块拟合的Te与Tref(转矩指令)一起输入到PI转矩控制器，PI转矩控制器根据输入的Tref指令和ELM神经网络模块的输出Te调整iqref，通过MTPA模块查表，找到对应的iqref和idref并输出。 PI电流控制器接收iqref和idref，并在解耦装置的作用下输出vdref和vqref，之后将vdref和vqref转换成三相电压输入SVPWM转换器。PI电流控制器通过调整vdref和vqref，直到电机中的实际电流等于d，q轴电流命令(idref=id,iqref=iq)；同时，PI转矩控制器调整iqref，直到电机的实际预测输出Te等于当前转矩命令Tref(Te=Tref)，此时电机的输出转矩等于转矩命令Tref，最终控制电机运行。

3 仿真结果与分析

在测试ELM神经网络转矩观测器效果时，用BP神经网络转矩观测器作为对比实验，在电机仿真物理参数完全相同的情况下比较两者的效果。电机模型仿真参数设置如表1所示。

表1 仿真参数

电机仿真模型的转速从50r/min到1500r/min递增，空间相位角β值为0～π/2，训练时电流增幅为1 A，测试时电流增幅为0.5 A，即用多种转速和更精确的电流值来验证ELM和BP神经网络的拟合性能。从传统PI仿真模型生成的数据中随机抽取170条数据作为测试集，两模型测试效果如图6所示。

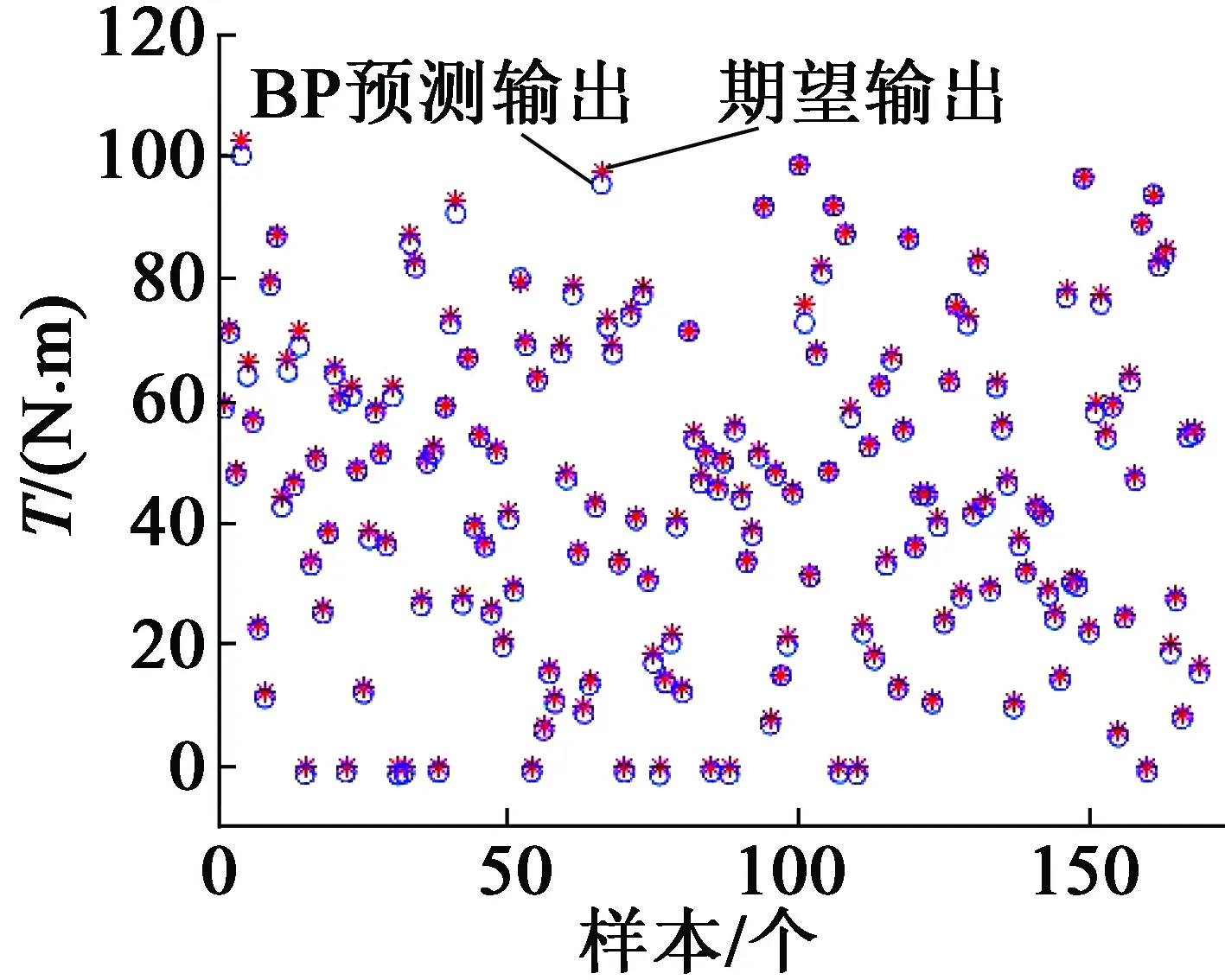
(a) BP神经网络

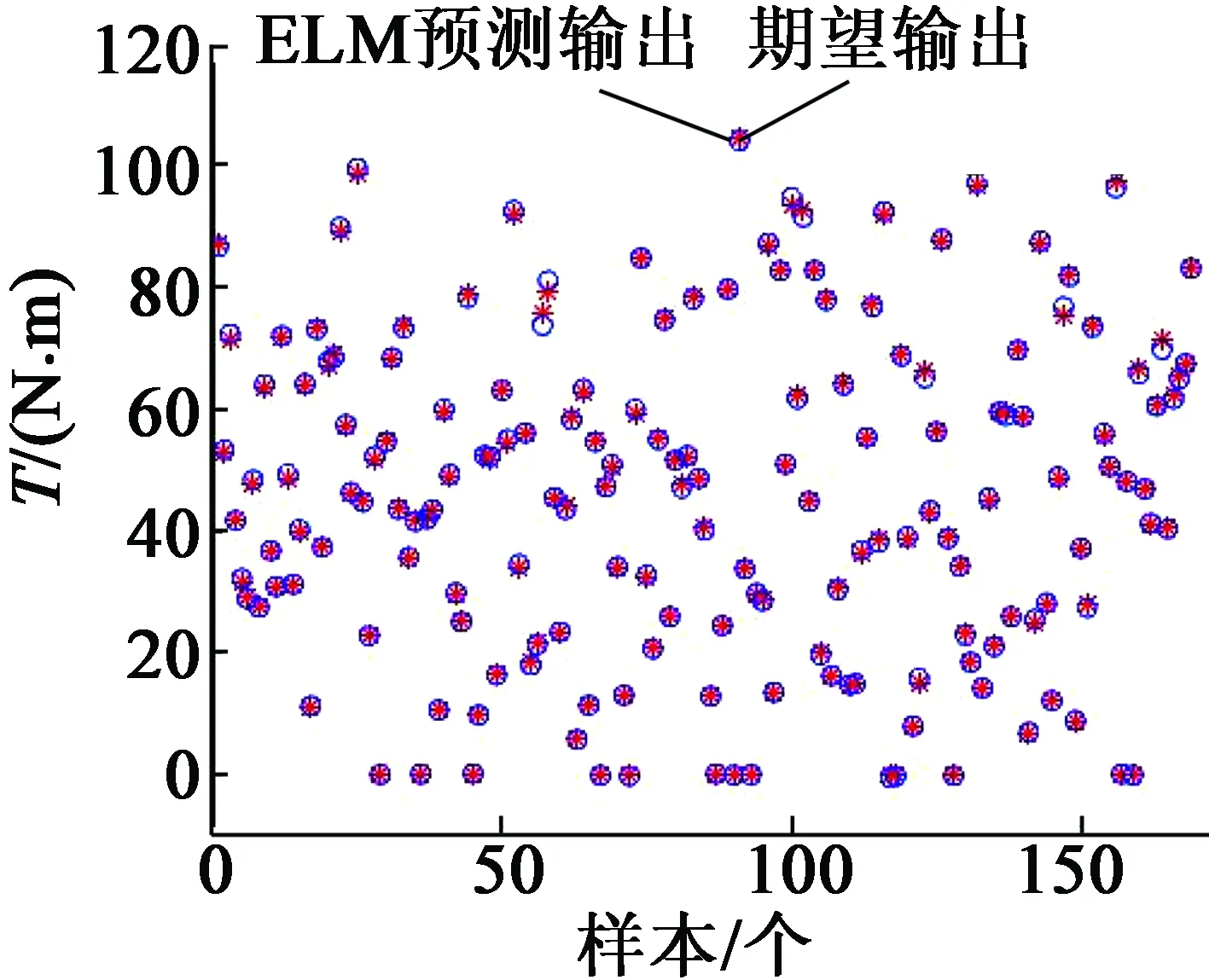
(b) ELM神经网络

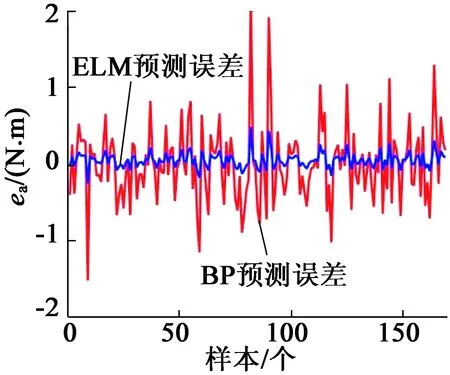
(c) 误差比较

经计算，BP和ELM模型的精确率分别为95.35%和97.4%。其中，BP神经网络参数：学习率为0.001，激活函数为sigmoid，损失函数为MSE、神经元节点个数150个，训练步数200步；ELM神经网络参数：激活函数为sigmoid，神经元节点数150个。

对比发现，ELM神经网络在同等参数设置条件下效果明显优于BP神经网络。虽然ELM测试结果精确率略高于BP，但其训练时间远低于BP，故本文采用ELM神经网络去实现转矩观测。

如表2所示，通过试凑法来调整ELM网络隐藏层节点发现，隐藏层节点数并非越多越好。从测试的精确率可看出，当隐藏层神经元个数逐渐增加时，预测精确率呈先增后减的趋势，当节点为169时，精确率最高，远高于BP的91.35%，故本文采用了169个隐藏层节点的ELM神经网络。

表2 ELM神经网络预测精确率

ELM神经网络观测器的仿真表现如图7所示。其中，图7(a)是在电机转矩突变的情况下，电机实际转矩和ELM神经网络拟合的转矩输出对比图，由此可看出，该观测器具有较好动态性能。图7(b)是电机以恒定的转矩值和转速值起动并平稳运行时，电机的静态转矩输出和ELM神经网络转矩观测器的输出几乎完全吻合，在起动0.02 s左右达到稳定值，并且平稳保持，这说明该观测器具有较好的静态表现。图7(c)是在转矩命令从零开始随时间稳定增长，到60 s时电机实际转矩和ELM神经网络转矩观测器输出值的曲线图。从图7(c)可以看出，观测器输出值可以较好地跟随电机实际转矩的变化，具有较好的全局稳定性。

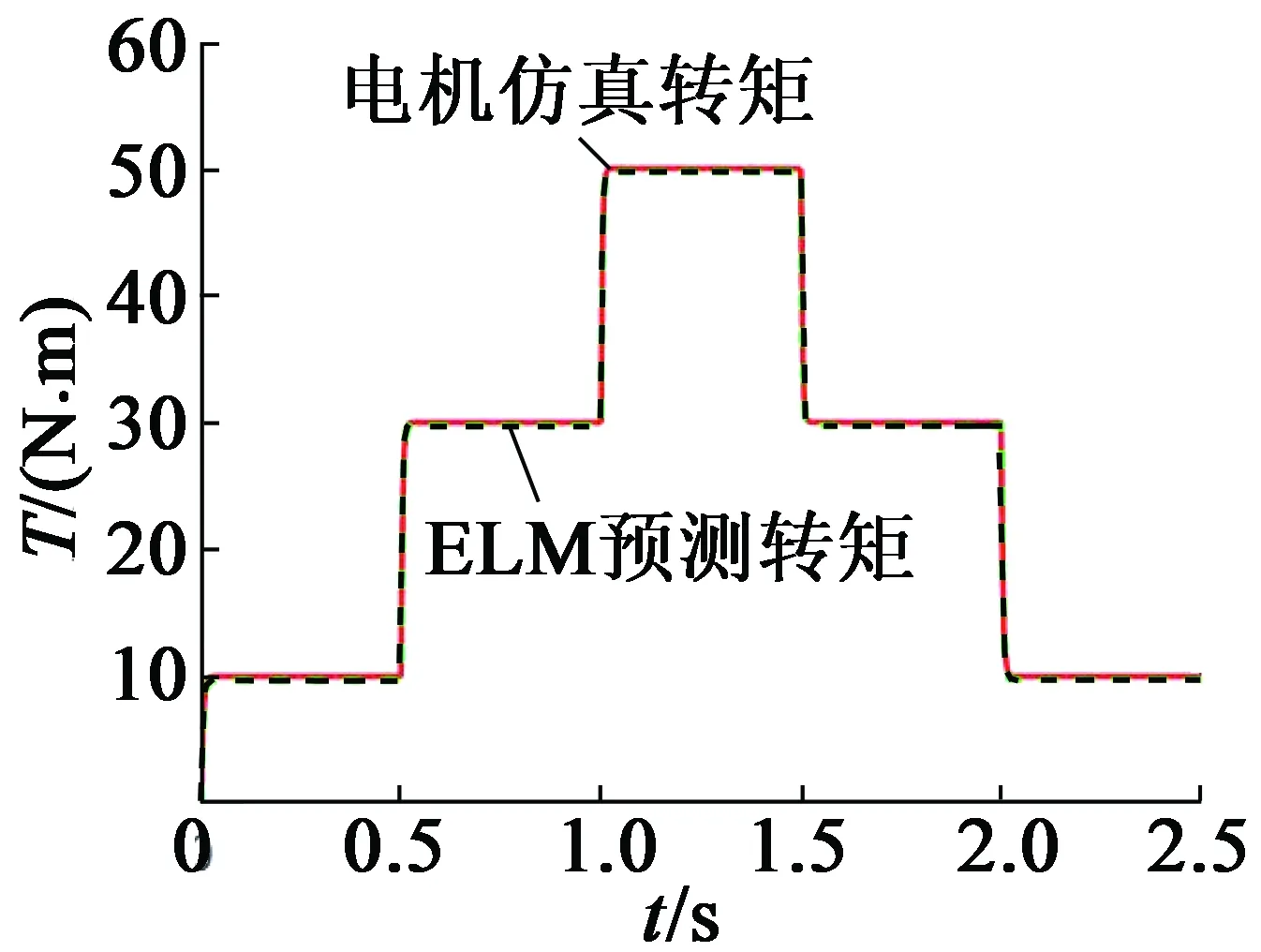
(a) 观测器动态转矩输出结果

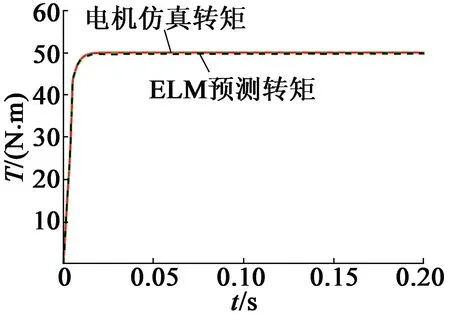
(b) 观测器定值转矩输出

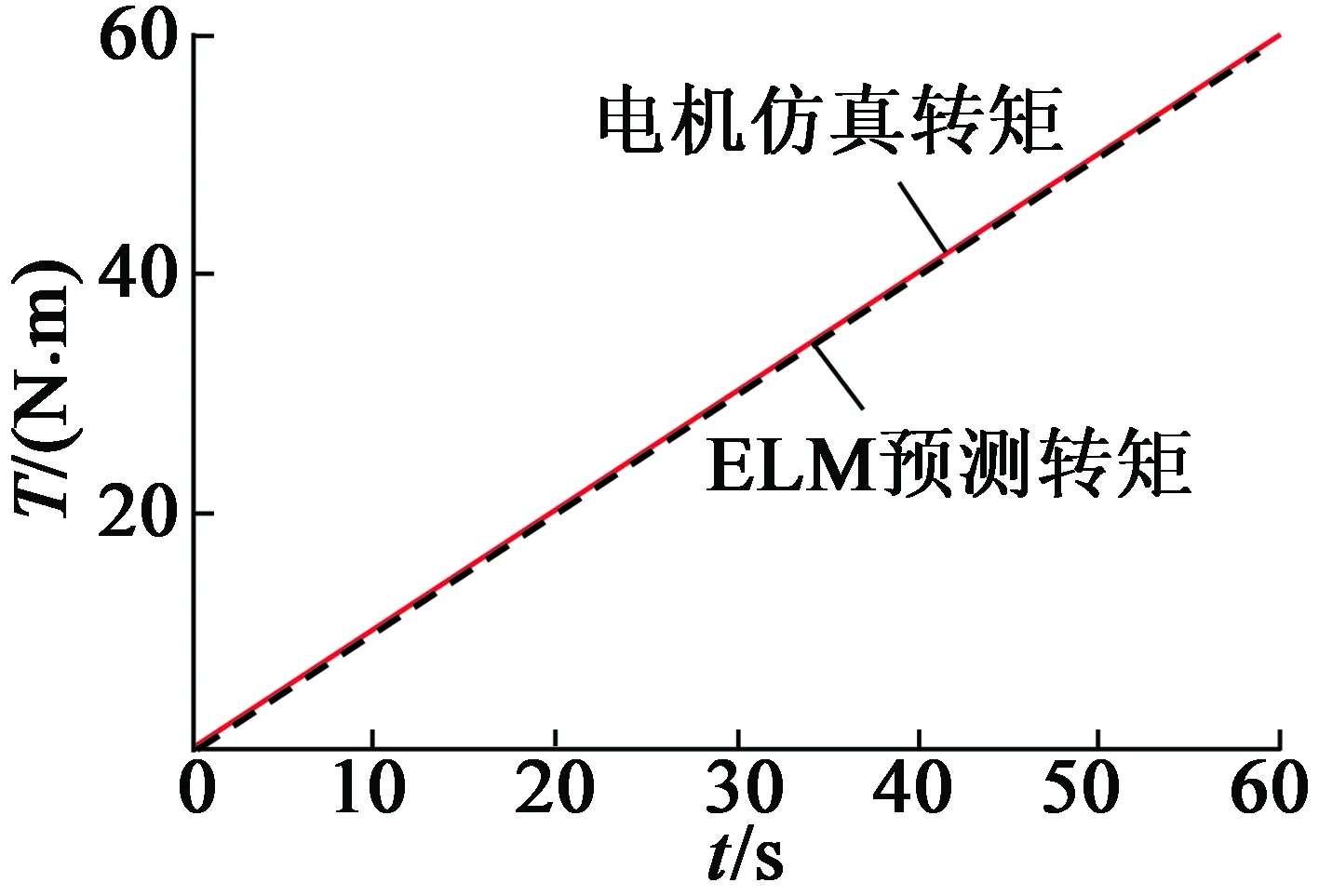
(c) 观测器渐变转矩输出

4 实验结果与分析

如图8所示，实验平台由电源、转矩转速观测器、驱动控制板、控制箱、DSpace、伺服控制器、电机平台和一台电脑组成。其中电机平台由ZH07扭矩传感器、130ST-M10015LFB永磁同步电机和一个底座组成。

图8 实验平台实物图

130ST-M10015LFB永磁同步电机参数如表3所示。

表3 永磁同步电机参数

为了验证ELM转矩观测器的实验性能，在实验时设定两组实验：带预先训练好的ELM神经网络模块的模型(图5)和只用PI模块的模型。电机起动初始时刻负载转矩Tref=0，在t=2 s时加上10 N·m负载转矩，将此过程中产生的数据保存下来，并通过MATLAB画出1.9～2.1 s的物理曲线图，该实验结果对比图如图9所示。

从图9(a)和图9(c)中可以看出，在电机起动的扰动允许范围内，ELM模型有效地降低了转矩脉动，经计算，转矩脉动大约降低90%，具有较好的转矩波动拟合能力。并且从图9(b)和图9(d)中可以看出，ELM模型较传统的PI模型有更精准的动态拟合能力和较好的抗扰动能力。

(a) PI模型的电机转矩

(b) PI模型的三相电流

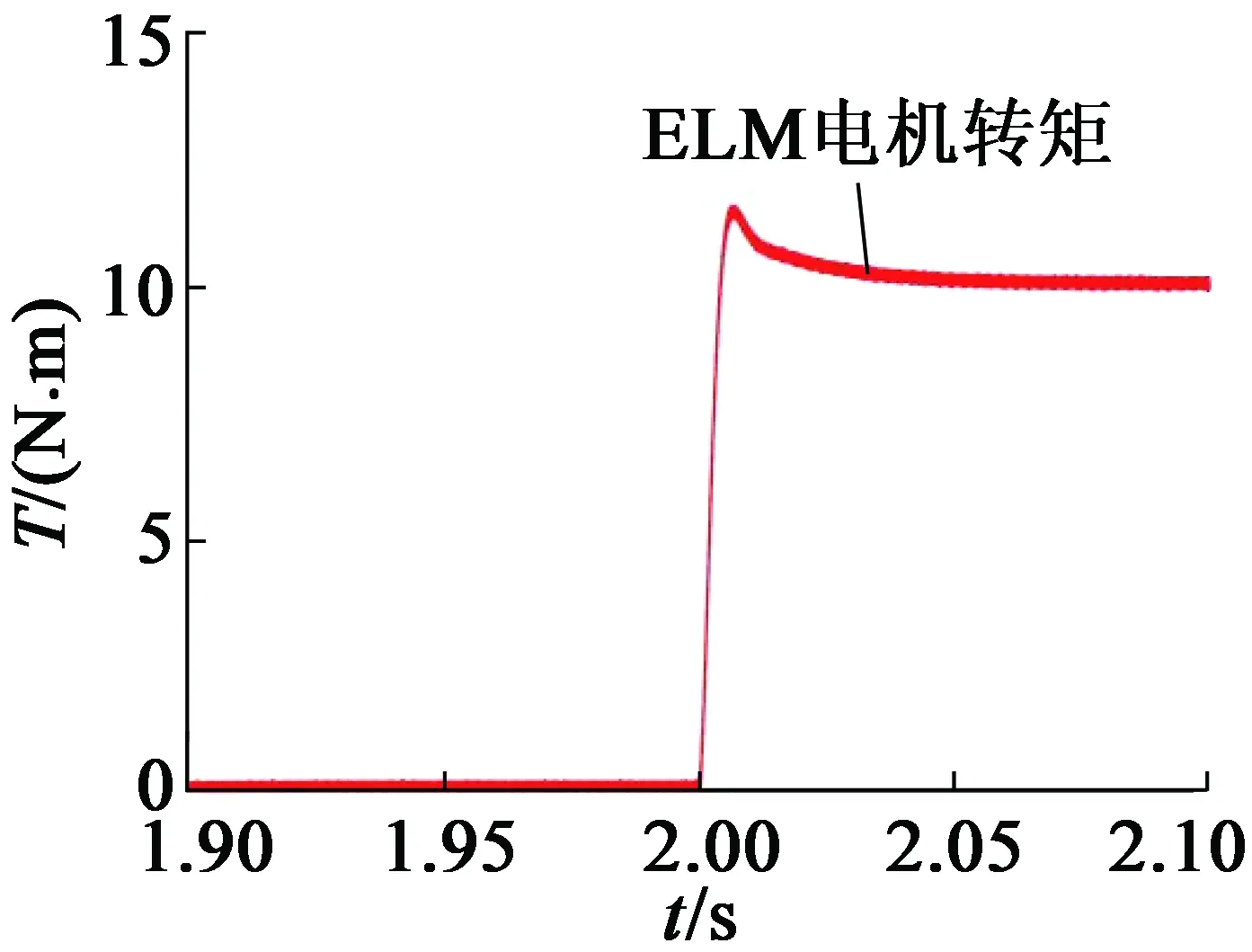
(c) ELM模型的电机转矩

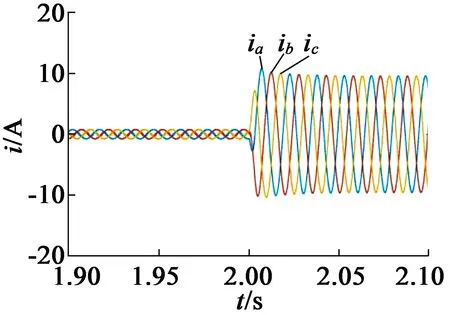
(d) ELM模型的三相电流

5 结 语

使用高精度、快响应的转矩观测器来精确观测IPMSM的转矩对于电机控制非常重要。由于电机参数是时变的，传统的基于数学模型的方法计算误差较大，影响系统性能。在本文中，电机转矩直接由ELM神经网络预测，通过训练神经网络，它可以精确预测电机的转矩。ELM神经网络结构简单、精度高，而且较传统BP神经网络速度能更快、更好地实现电机转矩的动态观测。仿真和实验结果表明，该系统具有良好的转矩观测能力和转矩波动抑制能力。