基于双线性插值的印刷图像旋转算法实现

李承轩，舒忠

（荆楚理工学院，荆门448000）

0 引言

印刷图像旋转操作，主要用于印刷页面的排版设计。在当前的排版软件中，图像旋转算法多为采用三次卷积算法对旋转后的图像进行插值补偿。而对于印刷图像后续进行RIP输出操作，由于使用了计算量较大的算法，会导致输出时速度降低。

在数字图像处理中，对图像进行旋转操作，图像占用的空间位置必定会变大[1]。这是导致印刷图像在RIP输出时运行速度降低的主要原因。图像旋转基本运算过程包括：矩阵旋转→前向映射→反向映射（包括图像插值运算）三个主要步骤[2]。图像旋转需要对其过程进行描述，并不只对旋转结果进行运算，图像旋转的过程中，图像占用空间的面积随时都在发生变化，运算过程对此都进行了统计，这是图像旋转运算时需要大量空间的主要原因。同样，图像的平移算法也需要对图像平移过程中图像占用空间的面积进行统计，如果排版页面不能提供足够的运算占用空间，也是无法将图像移动到需要地位置，特别是整个排版区域的边缘位置。

图像旋转的数学运算实现是以图像的中点为原点，围绕原点对图像进行一定角度的旋转[3-5]。其变换的MATLAB实现流程为：读取图像→构建图像矩阵且对矩阵进行初始化（初始值设为0，表示为黑色）→设置该图像的旋转角度（如：α=-15*3.1415926/180.0，表示为逆时针旋转15°）→定义旋转变换矩阵（H=[cos（α）-sin（α）0;sin（α）cos（α）0;0 0 1]）→使用矩阵乘法计算旋转坐标的位置（双循环计算旋转图像的每一个像素位置）→给旋转后的每个像素进行赋值。

三次卷积插值是依据三次多项式S（x）计算最佳插值函数 sin（x）/x，其像素（x,y）的灰度值由其周围 16 个像素点的灰度值加权后获取[3]。三次卷积插值的MATLAB实现流程为：读图→转双精度浮点数据类型→构建图像矩阵并对矩阵进行初始化→设置旋转（或放大）参数→循环历遍所有空间像素点为灰度插值运算结果赋灰度值做准备→计算u、v值（指需要赋灰度值像素点与相邻像素点的横向和纵向距离）并确定起始像素点（指16个相邻像素中的第1个）的位置→循环计算相邻像素点（共16个）的插值系数→计算16个相邻像素点乘以插值系数后的灰度值和，并赋值于该像素点→使用同样的计算方法完成图像所有像素点的赋值→显示结果。

根据印刷图像处理的特点，在实际应用中，图像旋转后的插值补偿，根本没有必要使用三次卷积插值运算，使用双线性插值运算所产生的图像像素灰度值误差进行补偿，完全能够满足印刷图像输出的需要。本文在后面的内容中，将对其原因进行分析。

1 改进的图像旋转双线性插值算法实现

1. 1 算法思想

本文设计的改进算法主要思想是：在变换域中完成图像的旋转与插值运算。

使用变换域（频域）完成图像旋转与插值运算，可以减轻图像处理过程中的复杂度和计算量。傅里叶变换是最基础的频域变换，其他多数频域变换都是由傅里叶变换演化而来，例如：余弦变换和小波变换等。离散余弦变换，取的是傅里叶变换变换的余弦运算部分（复数的实部），而小波变换则是利用了短时傅立叶变换的原理，通过分窗实现频域变换[3]。通过对几个频域变换方法的比较，充分考虑运算效率和运算结果等因素，选择余弦变换为最佳频域变换方式。

图像旋转属于基本的图像几何变换，通常在空域中完成。本文设计采用一体化解决方案，选择在频域完成对图像的旋转与插值运算。

对图像旋转后的插值运算采用双线性插值方式。本文研究主要是解决印刷图像的处理，印刷图像是通过4色油墨实现对图像的复制，与图像原稿相比，其印刷结果永远追求的是接近原稿，很难实现超越原稿。从成像方式上看，数字图像由可见光组成，产生的颜色千变万化，而大多印刷只使用4色油墨去还原数字图像的色彩，本身就有一定的难度。因此，图像处理的过程，只要在质量控制的要求范围内，可以对处理要求进行适当的调整。在进行图像旋转时，使用双线性插值方式进行灰度值补偿，可以满足图像对印刷的要求。

1. 2 算法实现

本文设计提出的算法实现步骤：

（1）图像预处理：读取图像；转双精度浮点数据类型，以便于计算机实现在[0,1]以内的计算；将图像转换为矩阵表示等。如果原始图像还需要进行其他增强处理，可以在空域内完成相应的变换。

（2）空域转频域：将空域表示的图像转换为离散余弦频域表示，使用前文设计的离散余弦正变换函数完成。

（3）图像旋转：完成设置图像的旋转角度、定义旋转变换矩阵、使用矩阵乘法计算旋转坐标位置、旋转后的每个像素赋值等操作。

（4）图像插值：循环历遍所有空间像素点、计算u、v值（需要运算的像素点与相相邻像素点之间的横向和纵向距离）并确定起始像素点（指4个相邻像素中的第1个）的位置、使用计算公式完成灰度值计算并对所有像素点赋灰度值等操作。

（5）余弦逆变换：使用MATLAB提供的idct2（）函数完成图像从频域向空域的转换。

（6）显示运算结果：使用MATLAB中的imshow（）函数显示进行变换后的结果。

其中：

对于双线性插值计算，将选取4个邻域像素点进行赋值的计算模板。双线性插值的MATLAB实现流程为：读图→构建图像矩阵并对矩阵进行初始化→设置旋转（或放大）参数→循环历遍所有空间像素点为灰度插值运算结果赋灰度值做准备→计算u、v值（需要运算的像素点与相相邻像素点之间的横向和纵向距离）并确定起始像素点（指4个相邻像素中的第1个）的位置→使用计算公式完成灰度值计算并对所有像素点赋灰度值→显示结果。

另外，对图像进行旋转有两种方式：一种是以坐标系为基准的图像旋转，另一种是按图像中点为基准的旋转。本文采用以图像中点为基准进行旋转，在进行旋转前，先将标准的平面坐标（平面坐标1，原点为图像左上角像素点）转换为图像中点平面坐标（平面坐标2，原点为图像中心像素点），然后进行图像旋转和插值计算，完成计算后再返回标准平面坐标中表示该图像。

算法的核心MATLAB代码如下：

……

T1=size（M,N,RGB）;%将图像转换为M×N的矩阵表示，图像模式为RGB。

M1=round（m*abs（cos（JD））+n*abs（sin（JD）））;%计算图像旋转后的行数，JD为旋转角度，round为四舍五入取整后的计算结果的MATLAB函数，abs为取绝对值后的计算结果的MATLAB函数。

N1=round（m*abs（sin（JD））+n*abs（cos（JD）））;%计算图像旋转后的列数，round为四舍五入取整后的计算结果的MATLAB函数，abs为取绝对值后的计算结果的MATLAB函数。

T2=zeros[M1,N1,RGB];%定义旋转插值后的输出图像矩阵，并且矩阵中所有像素值为初始值0。

ZB1=[1 0 0;0-1 0;-0.5*N1 0.5*M1 1];%定义平面坐标1向平面坐标2转换的运算系数矩阵ZB1。

ZB2=[1 0 0;0-1 0;0.5*c 0.5*r 1];%定义平面坐标2向平面坐标1转换的运算系数矩阵ZB2。

K1=[cos（JD）-sin（JD）0;sin（JD）cosd（JD）0;0 0 1];%定义图像旋转的变换矩阵K1。

K2（i,j,:）=（1-u）*（1-v）*T1（i,j,:）+u*（1-v）*T1（i,j+1,:）+（1-u）*v*T1（i+1,j,:）+u*v*T1（i+1,j+1,:）;%进行插值运算，定义图像插值运算的变换矩阵K2。其中，在图像转换为双精度浮点数据类型后，i、j分别为像素点横向坐标和像素点纵向坐标的整数部分，u、v分别为像素点横向坐标和像素点纵向坐标的小数部分。注意：在需要将图像转换为双精度浮点数据类型进行处理时，在频域完成相应的处理不仅可以大大降低处理的复杂度，还可以提高运算速度。

T2=[i j 1]*ZB1*K1*K2*ZB2;%此为主体变换公式，对原始图像依次进行平面坐标1向平面坐标2转换、旋转变换、插值运算和平面坐标2向平面坐标1转换（注意是依次），将运算结果图像的矩阵定义T2。

可以在K2和T2的计算过程中，使用离散余弦变换。

……

2 仿真实验与结果分析

2. 1 实验方法及目标

通过对方正飞腾（选用的一种国产排版软件，用于比较分析）中的旋转插值算法进行仿真，与本文设计的仿真算法进行比较，验证本文设计的算法与方正飞腾旋转插值算法结果相近，但本文设计的算法运算量小。对实验结果的评价以客观评价为主，采用峰值信噪比作为比较参数[6]。由于本实验验证的是低层次算法挑战高层次算法的结果，因此，实验结果方面，只求接近，不求超越，但在算法运算复杂度和运算量方面，要求占有绝对优势。

2. 2 实验过程

通过对实验图像进行测试，使用本本文提出的图像旋转方法得到的变换后的图像如图1所示，图像旋转角度分别为-30°和-90°。使用方正飞腾的图像旋转方法（其图像旋转是在二维离散傅里叶频域采用三次卷积插值实现）的变换后的图像如图2所示，图像旋转角度也分别为-30°和-90°。

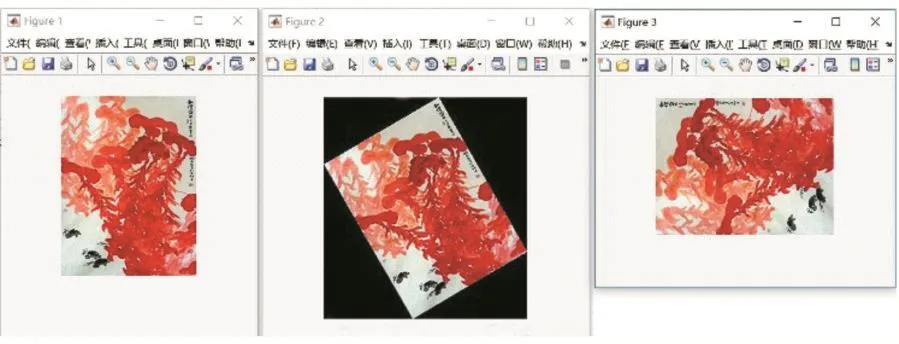
图1 本文设计的图像旋转插值算法测试结果

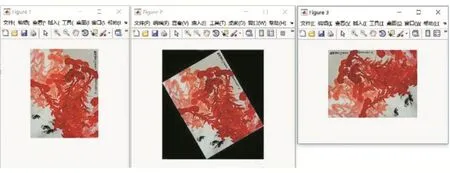
图2 方正飞腾的图像旋转插值算法仿真测试结果

2. 3 客观评价结果

两幅图像峰值信噪比计算的MATLAB实现流程为：读取图像→图像转为双精度浮点数据类型表示→分离R、G、B三色通道，每个通道都视为单个灰度图像→计算两幅图像各通道的灰度均值差→所有通道图像转换为矩阵表示→计算两幅图像R、G、B三色通道的峰值信噪比→取两幅图像的R、G、B三色通道峰值信噪比的平均值为两幅图像进行比较的峰值信噪比。

对两种方法分别进行-30°和-90°测试的结果如图3、图 4所示。

图3 使用两种方法旋转-30°进行测试的结果

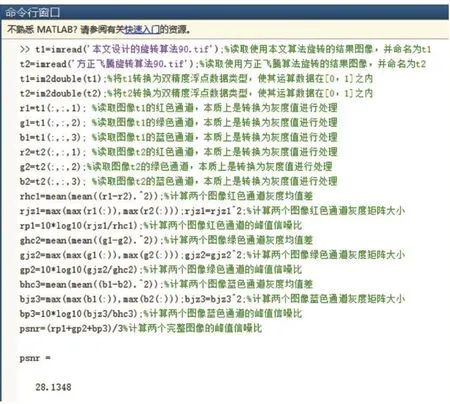
图4 使用两种方法旋转-90°进行测试的结果

2. 4 实验分析

实验中使用的两种旋转插值算法的主要区别在于：方正飞腾的图像旋转插值算法使用的频域转换平台为二维离散傅里叶变换，使用的插值方式为三次卷积插值；本文设计的图像旋转插值算法使用的频域转换平台为二维离散余弦变换，使用的插值方式为双线性插值。

二维离散傅里叶变换[7]的关键在于对复数进行计算，图像通过在复数平面内进行表示，对复数的实部与虚部进行运算，其基本函数为：ck[i]=cos（2πki/N），sk[i]=sin（2πki/N），ck[j]=cos（2πkj/N），sk[j]=sin（2πkj/N），通过欧拉等式进行变换后的复数的形式：

cos（x）=1/2ej（-x）+1/2ejx（复数实部）

sin（x）=j（1/2ej（-x）-1/2ejx）（复数虚部）

cos（y）=1/2ej（-y）+1/2ejy（复数实部）

sin（y）=j（1/2ej（-y）-1/2ejy）（复数虚部）

在以上基本上，最终形成二维离散傅里叶变换。

而二维离散余弦变换[8]则只需要进行二维离散傅里叶变换中的复数实部运算，因此，二维离散余弦变换的运算量是二维离散傅里叶变换一半，因此，本文提出的图像旋转插值方法，在计算复杂度和计算量上具有较强的优势。

根据前文论述，双线性插值选择了运算像素点周围的4个像素点作为参考值，进行补偿运算，而三次卷积插值则选择了运算像素点周围的16个像素点作为参考值，并使用卷积补偿运算。因此，本文提出的图像旋转双线性插值方法，同样在计算复杂度和计算量上具有较强的优势。

本次实验收集的数据主要是将两个图像的峰值信噪比作为客观比较的分析参数，两幅图像的峰值信噪比越高，说明两者的相似度越大，且标准衡量值在30dB左右。通常情况下，峰值信噪比主要用于一幅图像处理前后的对比，用于评价图像的相似度。在对一幅图像的处理前后进行比较时，相似度不高，才能说明图像处理的结果越明显，是图像处理的理想取值。但是，本实验是为了比较两种图像旋转后的结果是否相近，因此，其峰值信噪比理想取值是越高越好。通过与标准衡量值在30dB相比，采用方正排版软件的旋转插值和本文设计的旋转插值算法，在旋转-30°和-90°时，其结果都接近标准衡量值，且旋转-30°的结果要好于旋转-90°的结果。因此，研究结果与目标要求基本一致。此项实验结果获取的客观数据说明本文设计的旋转插值算法有效。

3 结语

本文设计的印刷排版图像旋转改进仿真算法，主要解决了印刷图像在制版输出时的速度缓慢问题，解决问题的关键来自两个方面：一是使用离散余弦变换替换广泛使用的离散傅里叶变换作为变换平台；二是使用双线性插值算法替换三次卷积插值。另外，在图像旋转时，使用以图像中点为基准进行旋转。以上这些改进手段的使用，大大降低了运算量。通过选用国内常用的方正飞腾排版软件与本文提出的算法进行仿真实验表明，本文提出的算法在大大减少了运行时间的同时，图像旋转效果与方正飞腾排版软件处理结果相近。