多源航迹融合中的数据有效性分析
魏浩然
(四川大学国家空管自动化系统技术重点实验室,成都 610065)
0 引言
数据有效性分析是数据挖掘中的一个重要方面,用来发现“小的模式”,即数据集中显著不同于其他数据的对象,在很多领域都有其应用,如气象预报、金融领域、网络入侵检测、药物研究,等等。对数据集进行有效性分析,能够找出那些异常的噪声数据,降低原始数据中的勘误影响,提高数据质量,从而提高计算精度。文献[1]将数据有效性分析应用到计算语言清晰度的实验中,并且对比了三种有效性检验方法的检验效果。文献[2]采用C4.5算法定义各个传感器所采集数据对目标传感器的支持度以决定目标传感器数据的有效性,结果表明,该算法能准确判断目标传感器数据的有效性和故障传感器在时域中发生的位置。文献[3]给出了仿真模型确认中的若干种数据有效性分析方法,用来保证仿真数据的正确性和可信度。文献[4]提出一种基于自适应阈值的轨迹异常点检测算法,有效检测出全部异常点,大幅度提高轨迹数据的质量。文献[5]系统地对目前国内外异常点检测算法进行了较为全面的阐述,并就这些算法在数据流挖掘中的可用性进行了研究与探讨。
针对多源航迹融合过程中的数据特性,本文考虑将数据有效性分析环节加入其中,通过基于距离的方法,检测并处理融合数据集中的异常数据,以提高融合结果的准确性。
1 多源航迹融合
多源航迹融合摒弃了单一传感器局限且不稳定的缺点,通过对同一目标的多个观测值进行归纳、综合,实现对目标更精确的识别,其处理过程[6]通常包含以下几个重要步骤:
(1)时空配准:从时间角度说,由于各传感器扫描周期不同,即便周期相同传感器位置不同各自所扫描到的目标时间也都不同,所以要将各个传感器报告的位置数据外推到同一时间点。从空间角度来说,每个传感器可能报告大地坐标、极坐标、直角坐标,坐标中心也有可能不同,融合之前需要将这些位置数据换算到同一公共坐标系下。
(2)数据关联:其目的是为了寻找量测值之间的联系,通过数据关联我们可以将来自不同传感器的同一目标的位置信息进行匹配,保证后续融合处理的合理性与正确性。
(3)融合估计:将融合关联表中的各个位置信息纳入计算,通过某种算法得出最终的状态估计值,常见的航迹融合算法有加权平均融合法、自适应加权平均融合法等。
通过上述流程可以将来不同雷达探测到的来自同一目标数据的进行综合,从而得到该目标更确的状态。
融合估计的要点是要求参与估计的信息尽量准确,任何一个误差大的观测值都会对目标飞行状态的估计产生影响。一方面,由于环境的复杂性和信号的不稳定性,传感器本身报告的目标位置信息可能存在较大的误差,另一方面,经过目标跟踪模块形成的航迹往往是一条锯齿形的,特别是没有经过滤波、平滑处理[7]的航迹,“锯齿现象”更加突出。若将跟踪航迹中的这种异常数据输入给多源航迹融合模块进行融合估计,势必会对融合结果产生不利影响。如图1所示。

图1 某时刻航迹关联情况
点迹A和点迹B虽然在关联门限内,但由于是航迹“锯齿突出”点,会与其他的点迹数据相距较远。经典的加权平均融合法计算公式如下:
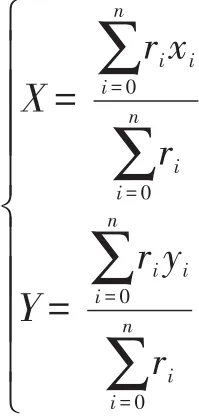
其中(xi,yi)代表第i个量测,ri为其权值。若航迹A、B权值很大的话,那融合估计结果受到的影响更大,所以消除这种异常位置数据十分有必要。
2 数据有效性分析
2. 1 标准差检验
对于上述问题,我们需要一种有效的方法去检测数据集中可能存在的异常值。在统计学中,数据有效性检测最常用的方法就是标准差检验法[8],用不一致性来测试识别异常。
假设在本周期有n个点迹数据加入到融合列表中。(Xi,Yi)为第i个点的位置信息,其中i=1,2,…,n。先计算这 n个点的中心位置。
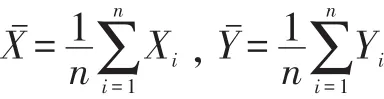

然后再计算这n个点到中心点的距离的标准差S。我们将离中心点三倍标准差距离的范围确定为有效数据范围,落在范围之外的位置数据为异常数据。标准差检验法简单、常用,但有效性检测的精度不高,效果一般,并且必须保证数据集符合某种特定分布才行,具有局限性。
2. 2 基于距离的算法
基于距离的方法是最先由Knorr和Ng[9]提出,其对异常点数据判定规则为:数据集T中的一个对象O称为异常点,如果它满足下列性质:数据集T中至少p*100%的对象与O的距离大于D。其实现算法流程如下:

该算法的重点是需要不断调整参数D和p,寻找一个合适的值,使其符合实际场景。若r偏大,会检测不出异常点;若r偏小,则可能把大部分数据都检测为异常点。参数的可调整性使得基于距离的检测方法能应用于不同场景。
2. 3 异常数据处理
检测出异常点后,我们需要考虑如何处理这些异常数据,一般有邻值替代法,均值替代法或者直接剔除法[10]等。直接剔除法最为简单(后续实验中若不另外强调,默认采用直接剔除法),但是没有考虑到某些特殊场景,可能确实存在目标紧急情况下偏离轨迹的情况,异常点数据一定程度上也代表着真实数据可能偏向某一方的特性,所以理论上邻值替代法会更加适合,即选择一个离它距离最近的点进行替换。一方面,替代点与异常点距离最接近,替代前后引起的误差最小,另一方面,替代数据与异常数据具有相似性质,都是样本域的边界点。因此,采用邻近点数据替代异常数据是一种较好的处理方法。
3 实验结果及分析
用δ2代表报告位置与真实位置的距离方差,则δ2衡量了数据源的稳定性,δ2越大的航迹越容易出现锯齿点,δ2越小的航迹越贴近于真实轨迹。本实验模拟了12部雷达在同一时间段下对同一目标进行跟踪,总共持续 30个周期,δ2分别为(24.6,1.9,3.2,3.1,2.5,3.4,6.2,3.1,2.7,5.0,2.2,25.1)。
实验假设这12条模拟航迹都位于同一目标的关联航迹列表中,原始的方法只需把同一个周期内的12个点迹进行融合即可,改进过的方法则需要在融合之前对这些点迹数据进行异常点检测、处理。
我们在同一场景下进行了15次实验,比较原始处理方法、标准差检验法、基于距离的检验方法(在r=8,p=60%的情况下)三种处理方式下的最终融合效果。检测到异常点后将其直接剔除。15次实验的结果如图2所示。

图2 三种方法的融合结果误差比较
折线图中的每一个点代表着某一次实验下30个周期内融合结果与真值距离误差的平方和。从图2中可以看出,在大多数情况下,加入了数据有效性分析环节的融合算法计算出的结果与真值的误差更小,并且,基于距离的方法检验效果要强于标准差检验法。
为了验证哪一种异常点处理方式更合适,我们在基于距离的异常点检测方法下,对异常点分别进行了均值替代、直接剔除和邻值替代三种处理,15次实验对比结果如图3所示。分析可知,80%的情况下,采用邻近点替代异常点后,融合计算出的结果与真实位置的误差最小,而均值替代的误差介于直接剔除法和邻值替代法之间,直接剔除法的总体误差最大。
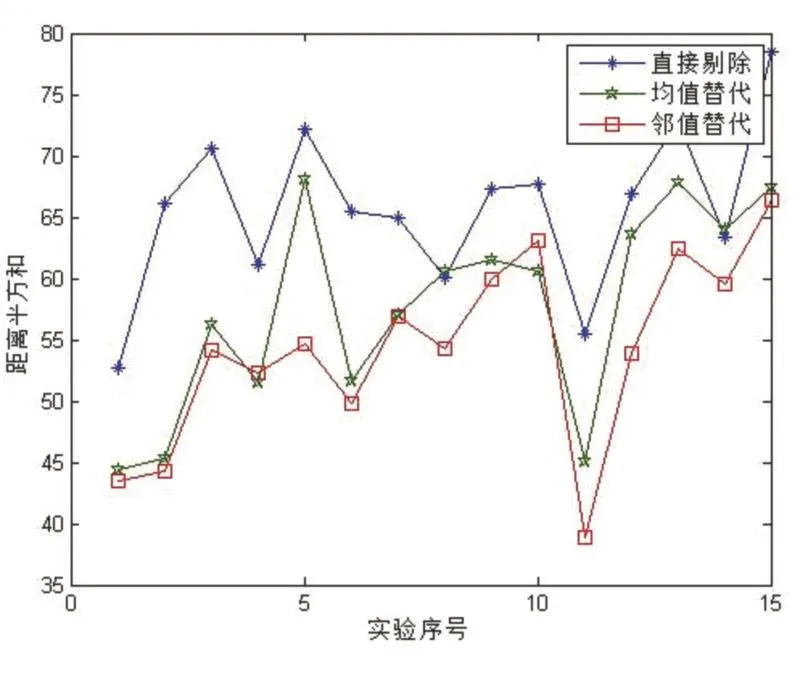
图3 三种异常点处理方法误差比较
4 结语
本文从提高融合结果精度的角度出发,提出了一种加入异常点检测、处理的改进融合算法,并对数据有效性检验方法、异常点的处理方法作出了对比和分析,实验结果表明,对于多源航迹融合,加入了异常点检测、处理环节的改进融合算法比传统融合算法的融合计算结果更加接近于真实值,并且基于距离的检测法要比一般的标准差检验法检测效果要好。在异常点处理方面,建议采用邻值替代法。

