基于共享自然近邻的自适应谱聚类算法

史佳昕，朱庆生

（重庆大学计算机学院，重庆 400044）

0 引言

聚类分析作为一种重要的无监督学习方法，是人们探索和认知事物之间内在联系的重要方式。聚类是将数据对象分为多个不同的子簇，使得同一簇中的对象之间具有较高的相似性，而不同簇中的对象差别较大[1]。传统的聚类算法如K-means算法和EM算法等，对凸球形的数据分布样本空间聚类效果好，但是对于形状为非凸形的样本容易陷入局部最优，聚类效果欠佳。谱聚类算法给聚类提供了一个新的思路[2]，是近年来提出的一类新型热门算法，与传统的聚类算法不同的是，它是基于图论理论，主要通过求解图的最优划分问题从而得到最优的结果，能够在任意形状的样本数据聚类并且收敛于全局最优解[3]。谱聚类在图像分割、文本挖掘、模式识别等领域被广泛应用[2]。

文献[4]提出一种基于自适应模糊均值和改进Ncut的谱聚类算法，但是有较高的计算复杂度。Ra[5]提出一种用加权PageRank选取具有代表性的点进行谱聚类，提高了其可扩展性。文献[6]提到用K-means的密度估计法来构成相似矩阵，提高了密度估计的准确性，缺点是参数过多。Li等[7]提出约束谱聚类的Nystrom方法，但是约束性参数会影响聚类结果。

在上述研究的基础上，借鉴共享近邻的思想，文中提出了一种基于共享自然近邻的自适应谱聚类算法。该算法利用自然邻产生的自然特征值与共享近邻结合，对相似度矩阵重新定义，使得对参数不再敏感，最后通过不同的实验验证了算法的有效性和准确性。

1 相关理论

1. 1 谱聚类算法基本原理

谱聚类将研究对象视为顶点，为顶点之间的边赋予权重，权重用对象间的相似度来表示。使用图分割解决聚类问题：寻找最优图分割的方法，使得分割之后连接簇与簇之间边的权重尽量小，簇内边之间的权重尽可能大。目前，常见的谱聚类算法有Ncut算法[8]和NJW[7]算法等。本文基于NJW算法阐述谱聚类的基本思想。设定原始数据集D={x1,x2,…,xn}∈Rd中的每一个样本点看作无向图中的顶点，记为V，根据样本点间的相似度将顶点之间的边E赋权值得到相似度矩阵W，由此构造了一个基于样本间相似度的无向加权图G=（V，E，W）。谱聚类算法可以归纳以下四个基本步骤：

（1）根据待聚类的数据集D生成图的相似度矩阵W，其中每个元素Wij可以用高斯核函数来表示，即：

其中：d(xi-xj)表示数据点xi和xj之间的距离，σ为尺度参数。不同的尺度参数可能会导致不同聚类结果，需人为设定，且聚类效果对参数很敏感，对于多重尺度数据集很难得到满意的聚类结果。

（2）计算拉普拉斯矩阵，并进行归一化，其中D为度矩阵；

（3）对L进行特征分解，得到前K个特征向量，并构建特征向量空间；

（4）利用经典的聚类方法如K-means对特征向量进行聚类。

1. 2 自然邻

自然邻是近几年才提出的一种新型的近邻概念[9]，区别于k-最近邻居和ϵ-最近邻居在于它不需要人为的设置参数，而是在不断的扩大邻域搜索范围的过程中自适应得出。该方法受到社会关系的启发，针对数据对象而言，假设数据对象y把x当作邻居，同时x也把y当作邻居，那么x和y互为自然邻居。如果数据集中每个点都有一个自然邻居，则可以达到一个稳定的状态。

定义1：（自然稳定状态）搜索数据集中每个数据对象 p∈D的k-最近邻居，k依次取1,2,3,…,N。若k增长至SUPK时，数据集D中的任意点都至少存在一个逆近邻，或者当数据集中逆近邻数为0的数据点不变时，称为自然稳定状态。

根据以上定义，自然邻搜索算法的过程具体如下：

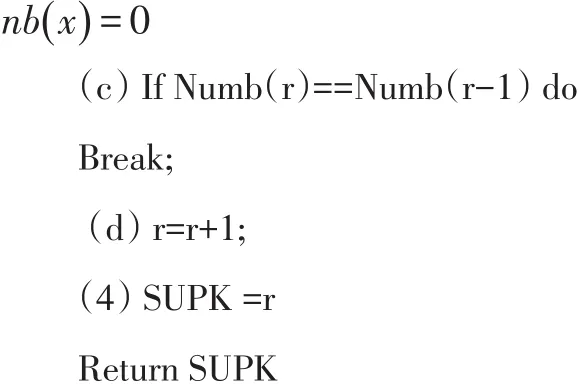
2 基于共享自然近邻的自适应谱聚类算法

2. 1 改进相似度度量

本文借鉴了Liu提出的共享近邻的概念[10]来重新定义了两点间的相似度。通过上述自然邻搜索算法得出的自然特征值，来确定数据集中每个点的邻域范围。

定义2：（数据点之间的共享近邻SNN）对于数据集D中的任意点i和点j，点i的SUPK近邻集合为3NL（i），点 j的 SUPK 近邻集合为 3NL（j）。数据集 D中的任意点i和j的共享近邻是两个点邻域的交集，表示为：

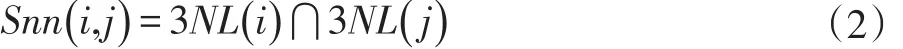
定义3：（基于共享近邻的相似度S）对于数据集中D中的任意点i和j，其共享近邻相似度定义为：

其中dist是点i和j之间的距离，相似度仅在点i和j出现在彼此的SUPK近邻时计算，否则，点i和j的相似性为0。

上述公式我们可以进行变换从而清楚地看到共享近邻相似度的含义。

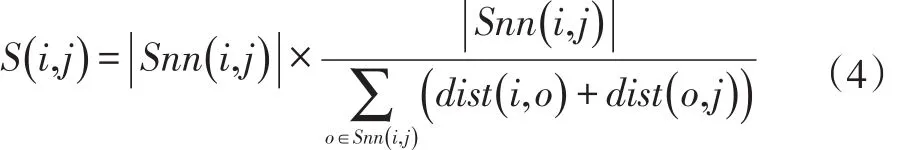
左边的一部分代表点i和j的共享邻域数，右边是点i和j到所有共享邻域距离均值的倒数，在一定程度上代表了这两个点周围的密度。通过同时得到共享邻域和两个点的密度，共享近邻相似度可以更好地适应各种变换的数据集。

经典的谱聚类算法中主要是高斯核函数来作为相似度函数从而形成相似度矩阵，使其更加接近原始的相似度矩阵。理想状态下，同一类中的点很相似，相似度接近1；反之两点不相似，相似度接近0。对比经典的高斯核函数计算相似度和本文提到的改进相似度，原始的高斯核函数，尺度参数的选择可能会导致不同聚类结果，需人为设定；针对所有数据点来计算相似度使用了统一的参数，会在螺旋数据集上无法识别相互缠绕的簇。而本文改进的相似度可以通过两点是否存在共享近邻来动态判断两点之间的相似度关系弥补了上述单一尺度参数的缺点，同时在共享近邻的基础上，还考虑到两点到共享近邻的距离，来反映两点周围的密度使得其包含真实的聚类信息，有利于可以发现真实的簇分布，得到正确的聚类结果。

2. 2 算法过程

根据以上定义，基于共享自然近邻的自适应谱聚类的过程具体如下:

输入：数据集D,聚类数C

输出：每个数据对象P的类标记

1.对数据进行自然邻搜索算法，得到SUPK值和每个点的邻域范围

2.根据共享近邻，构建相似度矩阵S

3.构建拉普拉斯矩阵,其中D为对角矩阵

4.计算前C个特征值所对应的特征向量

5.通过特征向量构成矩阵，用K-means进行聚类

6.将原始数据点分配到各自所在的类中，得到对应类标记

3 实验分析

3. 1 人工数据集

首先通过4个人工数据集进行实验来验证算法的有效性和可行性，其中Dataset1（Aggregation）表示一个包含7类的N=788的球状数据集；Dataset2（Moon）表示包含2类的N=1000的弧形数据集；Dataset3（Spiral）表示一个包含3类的N=312的螺旋形数据集；Dataset4（Db2）表示一个包含4类的N=315的条状数据集。下面给出具体的数据点分布图1。

为了验证该算法的有效性，分别在人工数据集和真实数据集上，对标准谱聚类算法（NJW）、自调节谱聚类算法（STSC）[11]、共享近邻的谱聚类算法（SNN-SC）[12]和本文算法（简记为SNaN-SC）进行了对比实验。

图1 不同算法的聚类结果

各算法在4个数据集上的聚类效果如图1，其中图1中第一列（a）是算法NJW的聚类效果，第二列（b）是算法STSC的聚类效果，第三列（c）是算法SNN-SC的聚类效果图，第四列（d）是算法3NS-SC的聚类效果。NJW算法需要人工设定σ值，按照文献给出的方法，设定σ的值为数据点之间欧氏距离变化范围dist=max(D)-min(D)的10%～20%，这 里 我 们 取σ=0.1dist来进行实验。STSC算法参数k为[2，50]中最优值，参考文献中建议的经验值p=7附近来进行实验[12]。SNN-SC算法中需要设定两个参数，p也取7，参数kd选取的范围值为5-25。

对比分析可知，本文提出的SNaN-SC算法在四个人工数据集上均能正确聚类；在Dataset1、Dataset2和Datase4数据集上，本算法聚类效果明显，而其他三个算法均出现不同程度的错误聚类；在DataSet3数据集上，NJW算法无法正确聚类，剩余三个算法聚类效果较好，但是在STSC算法结果上存在几个误差。NJW算法的相似矩阵完全是基于距离的，所以聚类结果在流行数据集上效果明显下降；STSC算法的相似矩阵考虑了密度和距离的关系，在数据集Dataset3上效果明显，在Dataset4上只能将一个范围内的数据分开，虽然考虑了数据点邻域的关系，但在弧形数据集上效果不好；同样针对流行数据集，流行间隙大且密度较高，SNNSC算法聚类效果理想，但也会受到参数的影响。而本文提出的算法将共享近邻来计算相似矩阵，而且只计算共享范围内的数据点，获得了更加符合实际情况的邻域信息，而且减弱了远范围点对聚类的影响。聚类结果充分可以体现本文算法的优越性。

3. 2 UCI真实数据集

此外本文还选取了3个UCI数据集进行实验，以验证算法的有效性。表3展示了真实数据集的特征。不同的评价标准会突出聚类算法的不同特性，本实验选取RI指标[13]和NMI指标[14]作为评价标准。

四种算法在RI评价标准下的对比实验结果如表4所示。RI的值越高，说明聚类效果越好。分析实验结果，发现：SNN-SC在Iris和Glass数据集上的RI指标相比NJW算法和STSC算法，取得了较好的聚类结果。而本文算法3NS-SC算法在三个数据集上取得很好的结果，得益于新的相似度量考虑自然领域和数据集点之间的局部信息对相似度的影响，有利于挖掘数据点间内在关系。

四种算法在NMI评价标准下的对比实验结果如表5所示。由于针对真实数据集很难找到合适的参数，而且其余三个算法的性能依赖于对参数的设定。本文算法SNaN-SC在四个数据集上较其他算法的NMI值都高。评价标准的侧重点不同或是数据集自身的特点导致Glass数据集上用RI进行评价时，SNN-SC性能最好，但是NMI评价时，该算法性能并不比我们的算法好。因此，从两种评价结果来看，相较于其他算法相比，SNaN-SC算法在真实数据集上具有更好的性能。

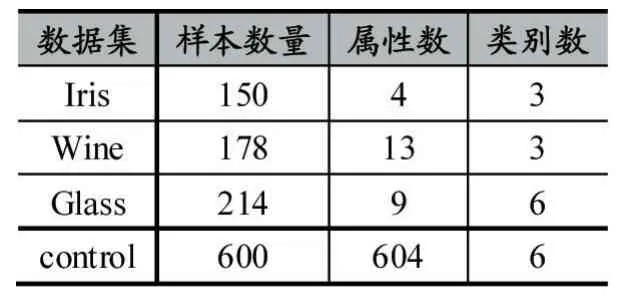
表3 UCI真实数据集

表4 算法在真实数据集上的RI对比

表5 算法在真实数据集上的NMI对比

4 结语

本文通过引入自然邻概念自动确定邻域个数，利用数据之间的共享近邻和距离信息重新定义了相似度计算，提出了基于共享自然邻的自适应谱聚类算法。该相似度能够有效描述数据之间的实际分布和内在联系。通过人工数据集和真实数据集的实验对比分析，表明该方法比其他算法具有很强的自适应能力，且聚类准确率较高。下一步的研究重心将放在运行效率的提高上。