基于FTA方法的浮式风机基础-塔柱系统定量风险分析

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300350)

0 引 言

海上风电场由复杂的大型风力发电机组成，需有高可靠性、可用性、可维护性和安全性。海上盐雾浓度高、湿度大，有碍机械和电气设备运行。风浪流的联合作用也为风机运行带来诸多潜在风险。海上风电大规模开发时间尚短、运行数据不足，不利于全面掌握其风险因素。已有研究表明，对于海上风电场，在一个项目的寿命中其操作和维护成本可占其电力成本的20%～30%[1]。采用合适的状态监测(Condition Monitoring，CM)技术，可检测许多故障，并在操作条件下对其进行控制[2]。海上风机发生的高概率事故主要出现在电气系统、传感器、叶片和变桨系统，损失严重的高停机事故主要发生在齿轮箱、主轴和轴承、塔柱、基础和偏航系统[3]。

PÉREZ等[4]通过对已有文献数据的汇总和比较得出叶片和齿轮箱问题往往导致较长的停机时间，且大型风机比小型风机更易出现故障。BAI等[5]利用故障树分析方法(Fault Tree Analysis，FTA)和失效模式与影响分析方法(Failure Mode and Effect Analysis，FMEA)相结合的分析方法对海上浮式风机吊装和运输风险问题进行分析和研究，并给出推荐的操作和管理措施。MARUGN等[6]采用临界方法的FTA分析，考虑天气因素，建立海上浮式风机各系统的故障树，并给出相应的维修管理方法。JIN等[7]系统地归纳和总结现有风机故障评价方法，并对各方法的应用进行分析，为工程应用和研究发展做出指导。万文涛[8]分析海上风机在运输和安装中的风险，研究表明考虑气候、潮汐、浪涌、地质等因素的制约，海上风电的运输安装风险和安装成本均高于陆地风电。郝二通等[9]研究基础与船舶的碰撞风险，运用LS-DYNA 软件数值模拟5 000 t船舶以2 m/s 的速度撞击单桩基础海上风机。

总体来看，目前对海上浮式风电系统的风险研究侧重于风险识别过程，在分析中更多地采用定性分析方法，部分定量研究主要针对零件或单一风险事件展开。同时，FTA的底事件概率确定对SCADA工程数据和专家打分的依赖性较强。鉴于此，本文采用数值计算与概率统计相结合的方法确定海上浮式风机基础-塔柱系统失效的概率，拓宽底事件概率数据来源，增强准确性，同时改进原有FTA方法，进行时域失效概率研究，并根据计算结果给出维修及风险控制建议。

1 基础-塔柱系统风险识别与故障树建立

引起基础-塔柱系统最终失效的因素相对较多，关系也较复杂，本文最终采用FTA方法进行基础塔柱系统的失效概率计算工作。FTA又称事故树方法，是安全系统工程中最重要的分析方法之一。FTA利用事件符号、逻辑门符号和转移符号等描述系统中各事件之间的逻辑关系，从而达到系统可靠性分析的目的。

1.1 塔柱-基础系统风险识别

基础-塔柱系统整体上可分为两部分，即基础-塔柱部分和偏航系统部分，其主要故障类型可分为机械结构损伤和材料疲劳损伤两方面。其中：浮式基础结构易发生缺损、裂纹等表面结构损伤；环境腐蚀将贯穿于结构寿命的全过程；结构故障主要为疲劳破坏；偏航系统主要故障形式为齿轮磨损、断裂和减速装置过热导致的效果不佳。基础塔柱系统的主要失效原因为风载荷与波浪力产生的交变应力及其作用下结构的一系列响应，特别是在结构内部连接出现问题的情况下，容易出现异常振动，增加系统运行风险[10]；偏航系统故障的原因主要包括建造安装和维护检查两方面，建造的精度不足会增加齿轮传动的磨损，而在运行中的润滑不佳又增强部件振动，缩短偏航系统整体寿命，影响风机系统运行[11]。

1.2 塔柱-基础系统故障树建立

在充分了解半潜型海上浮式风机故障类型与失效原因的基础上，参考相关研究给出的FTA模型[12]，建立海上浮式风机基础-塔柱系统的FTA模型，如图1所示，并针对结构过载损伤和连接疲劳进行详细的失效概率计算，结合OREDA数据库和已有研究对其他风险事件做出概率估算。

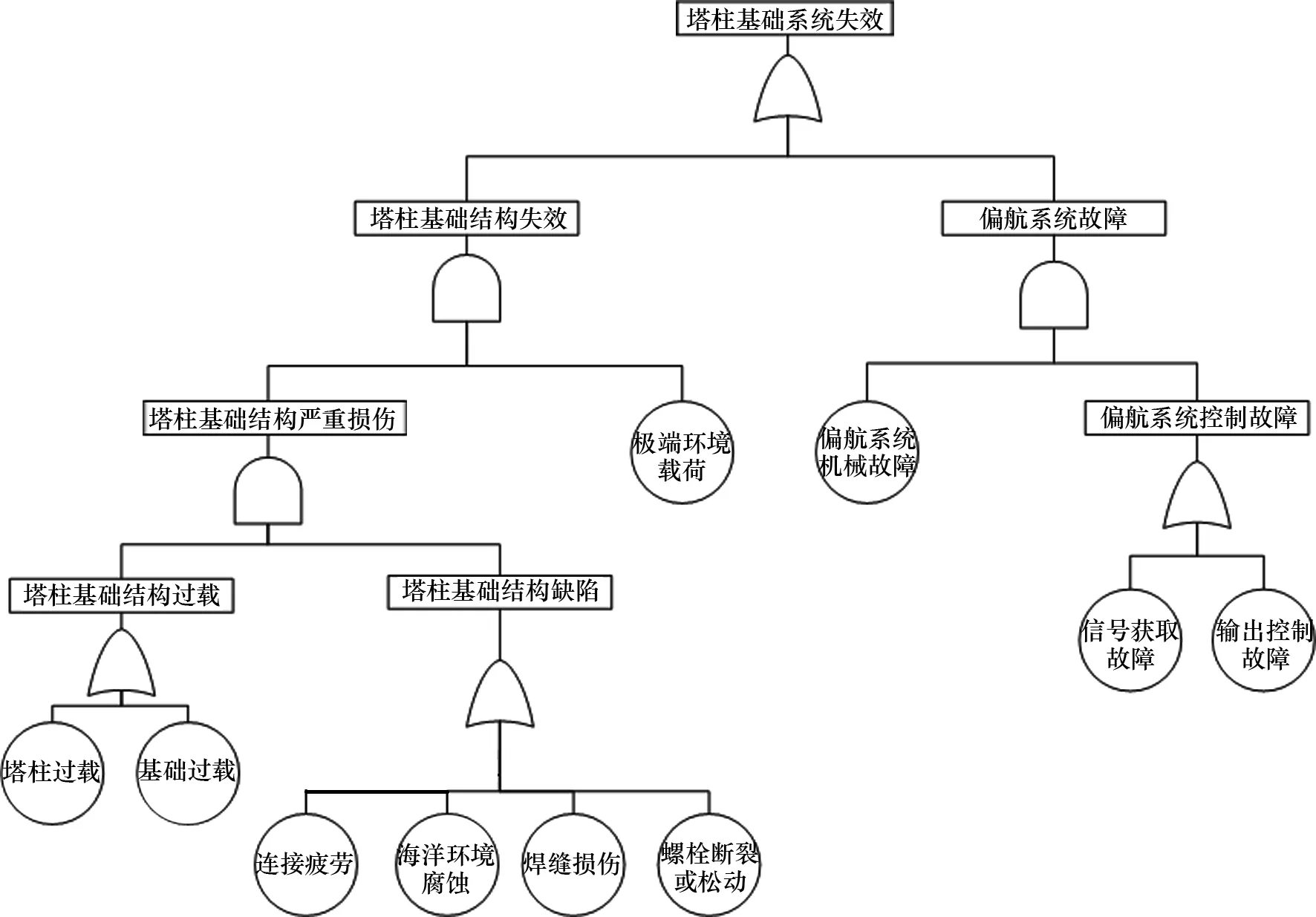
图1 基础-塔柱系统故障树模型

2 基础-塔柱系统失效概率计算

考虑到海上浮式风机基础-塔柱系统的风险类型和在分析方法上的区别，本文将塔柱基础系统的风险事件分为结构风险事件和非结构风险事件。

2.1 结构风险事件失效概率计算

在结构风险计算上采用有限元数值分析方法。弥补目前浮式风机风险分析缺乏工程数据支撑的缺陷，增加故障树底事件概率的来源，弥补通常依靠专家打分、数据库和风险等级等方法选取概率的精确性问题，更为结构设计阶段没有实际作业数据的情况提供风险评估方法。

2.1.1 塔柱-基础系统故障树建立

适用于FTA分析的概率分析模型大致可分为3类，即随机概率模型、时间相关概率模型和物理参数可靠性模型，而与结构相关的过载和疲劳分析通常采用物理参数可靠性模型进行概率模拟。其对数正态分布的可靠性表达式[13]为

(1)

式中：Ф表示正态分布；s为对数正态分布的形状参数，在该研究中取值为0.1[14]；k为许用应力，本文采用S355钢进行计算，安全因数取1.1，故k值为323 MPa；Xmax为最大应力。

国内外学者的分析研究给出动态可靠性模型计算公式为

Rt=exp[-(1-R)·α·t]

(2)

式中：Rt为结构的动态可靠度；R为式(1)静载荷作用下结构的可靠性；α为该载荷的年循环次数；t为服役时间，a。

2.1.2 有限元模型建立

采用有限元分析方法，以OC4半潜型浮式风机为研究对象，根据具体参数建立浮式基础三维模型，如图2和图3所示，具体有限元参数如表1所示。

图2 浮式基础三维视图(SESAM模型) 图3 浮式基础三维视图(ANSYS模型)

表1 有限元分析相关参数

2.1.3 相关载荷与边界条件计算

考虑浮式风机的工作特点，分别对额定工况、切出风速工况和极限工况下的3种波浪环境进行模拟，具体工况参数如表2所示。

表2 环境载荷计算参数表

根据《CCS海上移动平台入级规范(2012)》的风载荷及风倾力矩计算方法，分别计算在不同工况下的风载荷与风倾力矩情况，将极限风速下的结果汇总于表3。

表3 极端工况风压载荷计算表

在风载荷计算中，将锥筒型塔柱划分为8段进行计算，同时对中心立柱和浮筒水面以上部分风载荷进行计算。表中具体参数如下：D为构件直径(前者为上直径，后者为下直径)，H为构件顶端高度(基于水平面)，S为构件迎风面正投影面积，Cs为受风构件形状因数，Ch为受风构件高度因数，V为H高度处的平均风速，F为构件风压载荷，M为构件风倾力矩。

根据表2，采用谱峰因子为1的3个JONSWAP谱产生随机波，其波幅时域曲线如图4所示。根据结构动力学相关知识，一阶波浪力可表达为波浪幅值与波浪力传递函数乘积的形式：

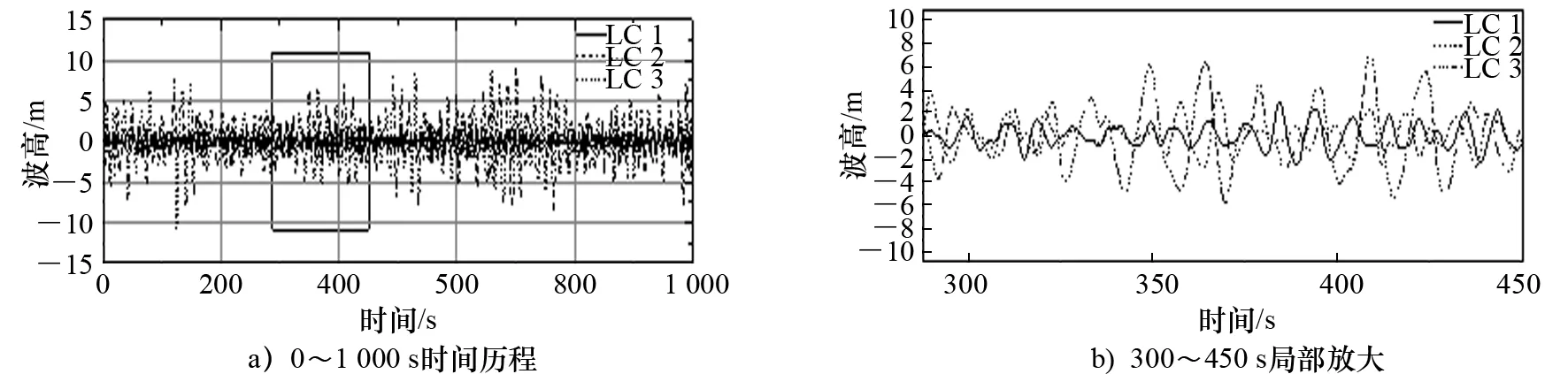
图4 波浪幅值时域曲线

式中：A为入射波波幅；ω为入射波角频率；β为入射波传播方向；φ为入射波的初始相位；t为时间；H(ω,β)为波幅-波浪力计算传递函数。通过SESAM HydroD计算半潜型浮式风机在0°浪向角下一阶波浪力传递函数，最终计算得到一阶波浪力时域曲线如图5所示。

图5 一阶波浪力时域曲线

计算作业海域出现的最大流速，考虑流速垂向分布，在极端海况下的流压计算如表4所示。

表4 极端海况下不同水深处的流压计算

位移边界：考虑浮式风机基础运动，在ANSYS瞬态分析中，将结构升沉和纵摇运动以动边界的方式施加到浮式基础上，尽可能真实还原结构的运动和受力状态，采用FAST计算其升沉和纵摇运动的时域结果，如图6和图7所示。

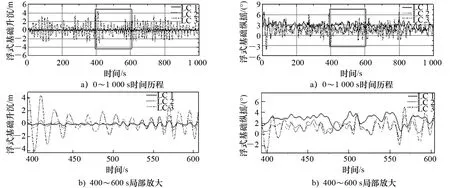
图6 升沉运动时域曲线 图7 纵摇运动时域曲线

2.1.4 结构失效概率计算

采用S355高强度钢作为材料进行分析，其屈服应力为355 MPa，弹性模量为208 GPa，泊松比为0.3，考虑工程实际，取安全因数为1.1，则许用应力为323 MPa。采用ANSYS瞬态分析，考虑塔柱与基础连接处作为危险节点，在3种工况载荷作用下，其应力变化如图8所示。图8表明，在定常风压作用下，塔柱的应力大小逐渐趋于稳定，最大应力出现在开始阶段。对基础过载事件，考虑主斜撑与浮筒连接处存在应力集中现象，以主斜撑-浮筒连接点作为危险节点，在3种工况下应力变化的时程曲线如图9所示。

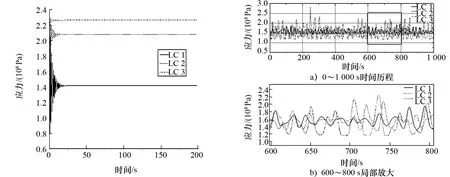
图8 塔柱基础连接点应力曲线 图9 基础-主斜撑连接点应力曲线

在疲劳分析中，采用Dirlik表达式作为危险节点应力时间历程雨流计数过程的概率密度函数，其表达式[14] 为

(4)

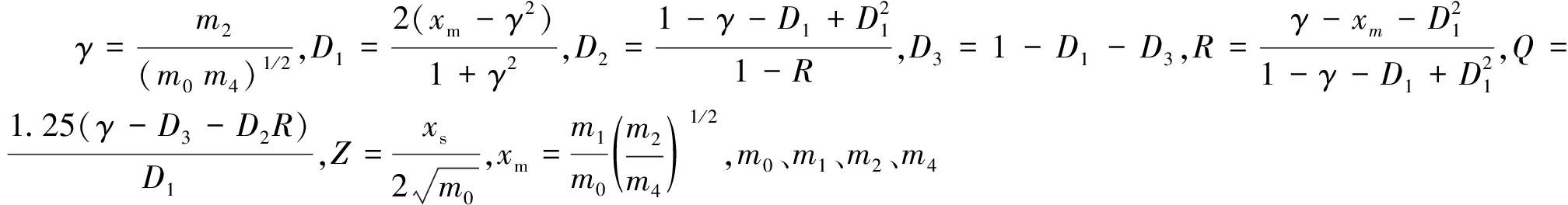
考虑疲劳极限服从正态分布，其概率密度函数可表示为

(5)

式中：μ为疲劳极限均值；σ为疲劳极限方差；xn为节点强度的统计值；V=σ/μ。结构的失效概率可表示为

(6)

采用雨流计数法，对3种工况下的主斜撑-浮筒连接点应力值进行统计，确定不同工况下的平均应力、应力幅值和各应力幅值的出现次数，对不同应力幅值的出现进行概率密度统计。图10和图11以在切出风速工况下的计算结果为例，给出主斜撑-浮筒连接点的平均应力与峰值应力统计图和循环应力概率密度曲线。

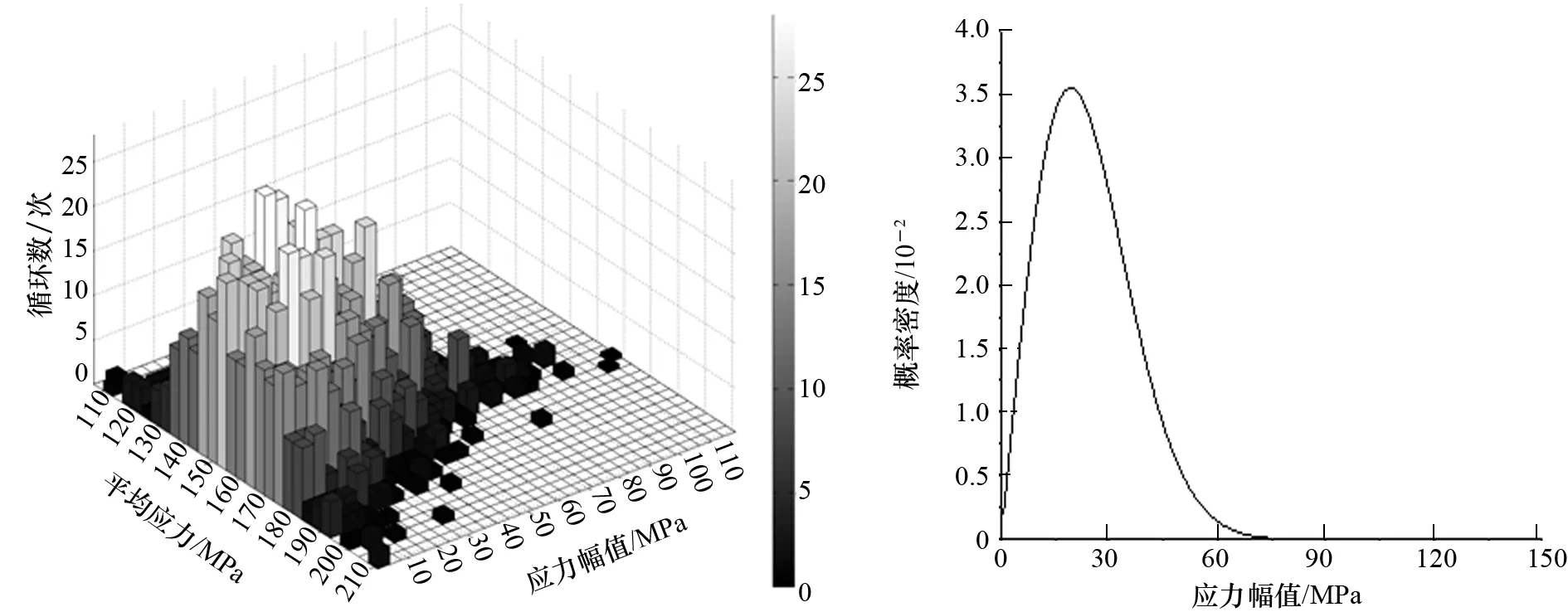
图10 LC 2下平均应力与应力峰值次数统计 图11 LC 2下循环应力幅值概率密度

采用应力结果统计方法，同时考虑选用材料的疲劳应力参数，将其代入式(6)进行疲劳时效概率计算，可得结构风险相关事件的失效概率，具体结果如表5所示。

2.2 非结构风险事件的失效概率计算

由于环境腐蚀事件贯穿结构寿命的全过程，且海洋结构物通常具备较好的防腐措施，而焊缝损伤会受人为因素影响，可认为二者的失效概率为最低等级，即0.000 1。极端风载荷可采用威布尔分布进行模拟[15]，在结构物自存状态的极限风速为51.5 m/s的情况下，可计算事件的发生概率约为0.002 6，则其年平均失效概率为0.001 39。关于螺栓的断裂和松动，其年失效概率应为0.001 53。对于偏航系统的机械故障，通过已有文献[16]的查阅，可知其年失效概率约为0.013。

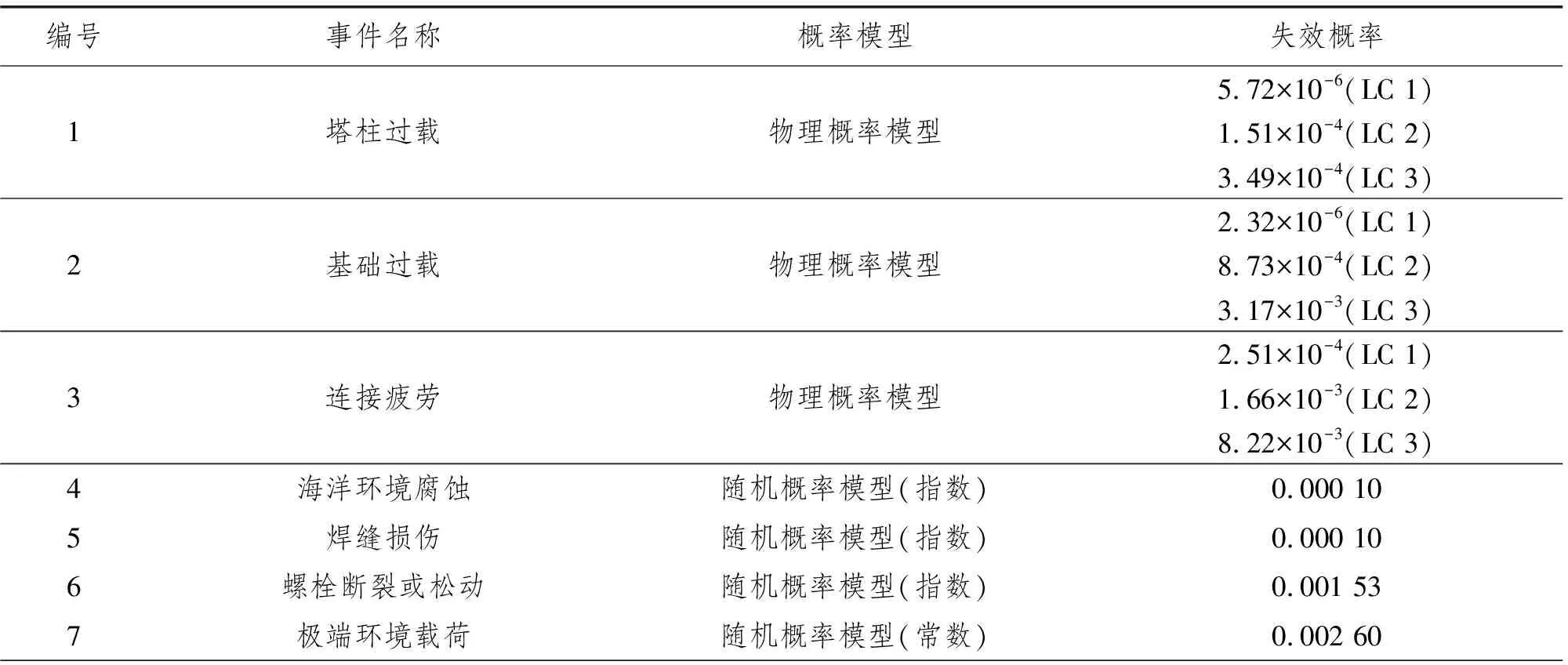
表5 基础塔柱系统基本事件的失效概率汇总表

续表5 基础塔柱系统基本事件的失效概率汇总表

3 全生命周期FTA定量计算

采用MATLAB语言编写时域动态故障树程序，基本逻辑运算基于传统的FTA方法完成，考虑部分风险事件的失效概率随服役年限的增长会明显升高，采用不同概率统计模型实现对失效概率的时域动态描述，其中物理方法的动态可靠性模型如式(2)所示，而随机指数型与随机常数型的可靠性模型如式(7)和式(8)所示：

Rt=e-λ·t

(7)

Rt=1-t·(λ/t)

(8)

式中：λ为事件的静态失效概率；t为服役时间。

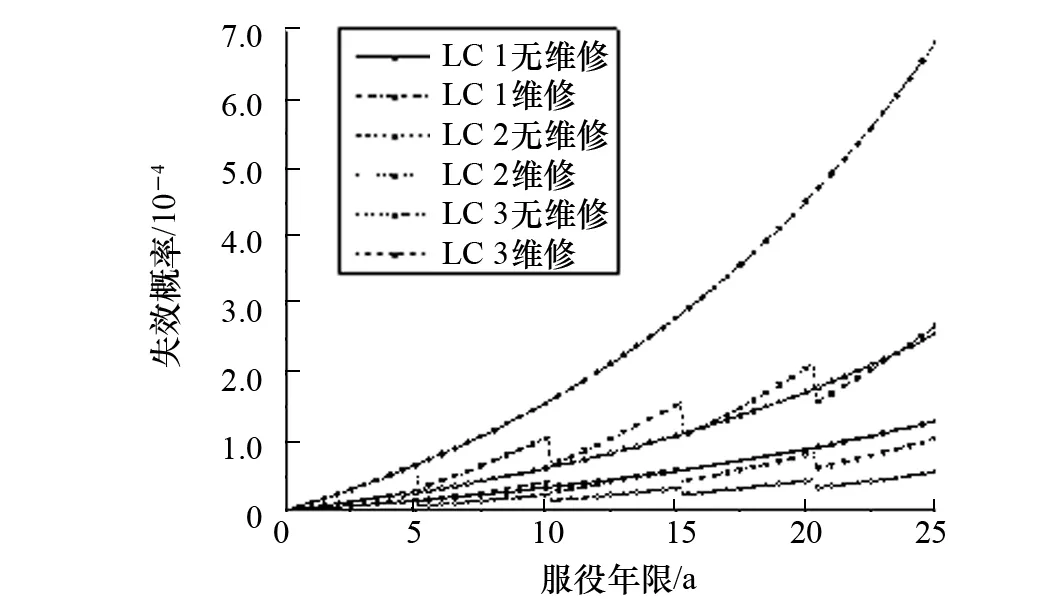
图12 失效概率对比

根据文献[17]提出的记忆强度还原模型算法，对定期维修进行初步研究，计算模型为

λt=(1-ρ)·λT

(9)

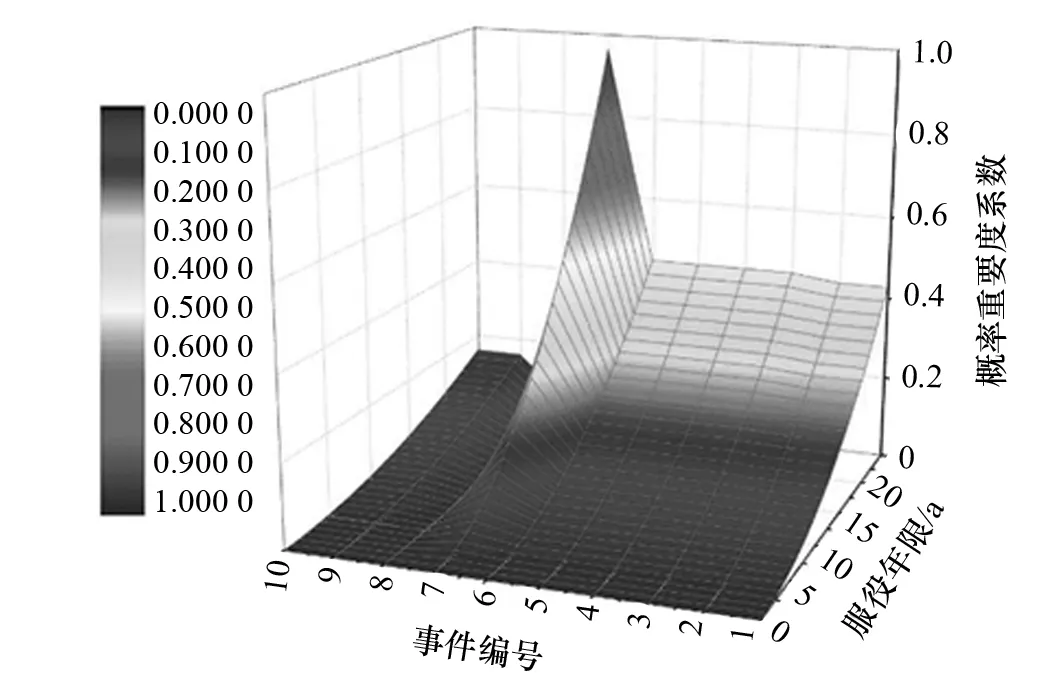
图13 底事件概率重要度因数变化曲线

式中：λt为修复后系统的恢复失效概率；ρ为不完全维修因数(越大则维修程度越高)；λT为维修前系统整体失效概率。本文计算采用该模型。

3.1 有/无维修情况顶事件发生概率对比

将前文计算得到的失效概率输入编写好的FTA时域分析程序，在考虑每5年维修一次、不完全维修因数为0.5的情况下，得到有、无维修状态下的失效概率曲线如图12所示。

由图12可知，水平轴浮式风机塔柱-基础系统在无维修的情况下，当达到服役年限时失效概率约为0.000 7，而在维修周期为5年的情况下，其最终失效概率下降约60%，仅为0.000 3，在很大程度上延长了塔柱-基础系统的使用寿命，提高结构使用的安全性。

3.2 基础-塔柱系统底事件概率重要度分析

考虑服役年限为25 a，通过时域动态FTA程序计算，可获得各底事件的概率重要度因数随服役年限的变化规律，如图13所示。

图13表明：在服役年限内塔柱基础系统整体上保持较低的失效率；事件7(极端环境载荷)在整个寿命周期内的重要度最突出，随服役年限增长，极端环境载荷对结构的危害性逐年增加；事件1～事件6随服役时间的增长，重要度逐年增加。这证明本文提供的关于结构的安全评价方法具有重要的实用价值。事件8～事件10的重要度随服役时间的增长并没有产生明显变化。

4 结 论

针对海上浮式风机基础-塔柱系统进行了有限元分析，采用瞬态分析方法和雨流计数法得到了结构风险事件的失效概率，有效弥补了因工程数据不足引起的概率来源不足问题，增加了风险分析的准确性。另外，完成了全面的失效概率分析，进行了各事件概率重要度分析。主要结论如下：

(1) 基础与主斜撑的连接点在风浪流联合作用下更易出现较大应力和疲劳风险，应在实际工程中加强对该点的应力监测和安全维护。

(2) 该风机的基础-塔柱系统整体结构风险概率较低，在服役年限内，最大风险概率约为0.000 7。在不完全维修因数为0.5的情况下，系统达到设计寿命时，其整体风险概率较不维修时下降约60%。

(3) 在服役年限内，极端环境载荷的威胁具有最高的失效概率重要度，应加强对服役海域的海况预报。随着风机服役时间的推移，结构安全性风险的概率重要度不断升高，建议服役时间较久的风机缩短可靠性检验周期，并加强结构风险评估工作。