基于动态故障树法的深海采油树系统定量风险评估

余建星， 任 杰， 杨政龙， 陈海成

(1. 天津大学 水利工程仿真与安全国家重点实验室， 天津 300072；2. 高新船舶与深海开发装备协同创新中心， 上海 200240)

0 引 言

深海采油树系统是深水油气田开发生产中极为重要的设备。深海的极端环境对采油树系统的影响非常严重，极易引起泄漏事故，造成海域的大面积污染[1]。因此,采油树系统的风险评估迫在眉睫。

故障树分析法规定了许多逻辑门和事件，并以图形的方式表示出各事件之间的逻辑关系[2]。传统的静态故障树基于的是静态逻辑和静态失效机理，因此其分析方法不适用于失效原因复杂且动态特征明显的深海采油树系统。对动态故障树的定量分析方法国内外学者已有较为深入的研究，如基于Markov模型的分析法[3]，Monte Carlo仿真法[4-5]，以及基于离散时间贝叶斯网络的分析方法[6]，等等。但上述理论多应用于化工及软件领域，在深海结构的风险分析中应用较少，而针对深海采油树系统的风险评估应用更是空白。

因此，本文将基于动态逻辑门的动态故障树理论引入深海采油树系统的风险评估，建立采油树系统的动态故障树模型，并根据现有的动态故障树Monte Carlo定量分析方法，对动态故障树进行定量分析，计算顶事件故障概率并分析基本事件的概率重要度和结构重要度系数，最后根据计算结果对采油树系统提出风险规避的建议。

1 深海采油树系统动态故障树建模

深海采油树系统由采油树主设备及其控制系统两部分组成，其失效可分为采油树树体及其控制系统的失效。前者失效又可以分为3大类原因，即人为影响H1、外部影响H2、防腐失效H3。

1.1 人为影响因素

人为因素对采油树系统的影响主要存在于制造过程H5和施工过程H6中。

H5的影响由部件生产失误H13和部件检验失误H40引起。H13可能来源于分析错误X2或者钢料加工失误H25，而H25可能由操作失误X1、分析错误X2以及偶然碰撞X3引起。H40可能来源于X1以及X2。

H6的影响来源于下水过程H14、安装过程H15以及储运过程X6中的失误。H14来源于X2和其他误操作H26，H26包括X1以及X3。H15来源于零件锁紧失效X4、密封失效H27、焊接失效H28以及H26，H27包括密封处有杂物X5、密封件损坏H41、密封处配合不完全H42，H41由X1或X3引起，H42由X2或X1引起[7]。H28由焊接施工和焊缝检验引起，焊接施工过程中的失误来源于X1或X3，焊缝检验过程中的失误来源于X1或X2。人为影响子树如图 1所示。

图1 人为影响子树及外部影响子树

1.2 外部影响因素

外部影响因素分为采油树体疲劳失效H7和突发冲击载荷H8造成的失效。

H7由两方面因素共同引发：首先是采油树部件的内因H16；其次是环境外因H17对采油树体的影响。诱使H16事件发生的因素主要有安装过程中拧紧力矩错误H29、产生了裂纹或尖锐缺口H30以及零件的形状尺寸不合理H31，这些都可能由X1和X2引起。诱使H17发生的因素可能由涡激振动X7、涡旋影响H32、波浪影响H33以及X6引起。地形有狭窄通道X8和海水雷诺数过大X9同时发生会引发涡旋的破坏；而X9或风力过大X10会引发波浪的破坏。

H8失效可能由以下因素引起：地震X15、锚击X16、风暴H18和土壤冲垮H19。H18由X10和采油树部件结构质量过小X11共同引发，即在X10与 X11同时发生时，采油树结构才会失效。造成H19这一事件发生的因素可能有X9、土壤沉积物过厚X12、土壤黏性降低X13以及土壤液化X14。外部影响子树如图 1所示。

1.3 防腐失效

防腐失效的途径有树内防腐失效H9以及树外防腐失效H10。

H10主要来源于缓蚀剂变质X22、阴极保护装置H21以及内壁防护涂层H22的失效。H22比较特殊，可以引入动态逻辑门中的优先与门。以产生酸性气体X20作为优先事件，黏结剥离X21作为其次事件，即当X20先发生，防护层X21后发生时，上层事件发生。H21主要来源于阴极屏蔽的发生H36或干扰/杂散电流的产生H37。H36由海管配重层内加强筋与管道短接H45或保护套管与管道短接H46引起，前者来源于X15或X16的影响，后者还需加H19的影响。研究H37时同样可以引入优先与门，以绝缘层破坏X18作为优先事件，其他管线的阴极保护系统失效X19作为其次事件，底事件先后发生时上层事件发生。

H9主要来源于H21以及防腐绝缘层H20的失效。前者的失效途径与H9中阴极保护失效的途径相同，后者的失效途径主要有微生物的破坏X17、土壤的松动H35以及防腐涂层应力开裂H34。H35可能由X12、X13以及X14引起，H34由H32或H33的破坏以及H8的破坏引起。防腐失效子树如图 2所示。

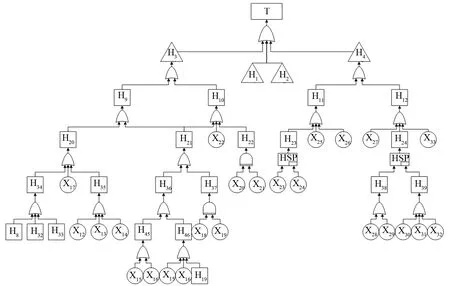
图2 防腐失效子树及控制系统失效子树

1.4 控制系统失效

采油树控制系统故障分为水上控制系统故障H11和水下控制系统故障H12。

H11包括液压动力单元H23、电源单元X25、电子控制系统X26，其中任意一部分发生故障都会导致顶事件的发生。在研究H23系统故障时，引入热备件门来描述其故障途径。液压泵系统失效X23作为其输入事件，水上蓄能器失效X24作为其热备件。只有二者均故障，液压动力系统才会失效。

H12包括脐带终端分配单元X27、水下控制单元H24和水下执行器X33，其中任意一部分发生故障都会导致顶事件的发生。在研究H24的失效途径时，同样可以引入热备件门来描述，即以水下控制单元的失效H38作为输入事件，失效安全执行单元H39作为其热备件。只有工作元件和备用件均故障，水下控制系统才会失效。引起H38的因素可能有回油皮囊失效X28或电液换向阀X29的失效。引起失效安全执行单元失效H39的因素可能有水下蓄能器X30、失效安全执行器X31以及压力补偿器X32故障，三者任一故障都会引发上层事件的发生。控制系统失效子树如图 2所示。

2 Monte Carlo仿真法

目前动态故障树定量分析的算法非常多，但是适用于深海结构的并不多。一是由于深海结构某些部件的故障概率随时间变化，并不服从指数分布，因此不能使用传统的Markov Chain法；二是深海结构动态故障树中的动态模块可能比较庞大，会面临着状态空间组合爆炸的问题。此外，多重积分的计算也是难题。

针对该问题，李堂经等[4]和杨恒占等[5]在动态故障树的定量分析过程中引入Monte Carlo仿真法，将多重积分等价为具有特定分布随机函数的期望值，设计随机试验以获得随机被积函数的样本。Monte Carlo仿真法可以归结为3个步骤：①构造或描述概率过程；②实现从已知概率分布中抽样；③建立各种估计量。

2.1 Monte Carlo仿真法动态子树的失效分布

(1) 优先与门

设其底事件x1和x2的发生时间为T1和T2，则其概率分布函数分别为G1(x1)和G2(x2)，那么顶事件发生时间的概率分布函数为GY(t)为

(1)

(2) 热备件门

热备件门主件与备用件同时运行且其失效分布函数基本相同；当且仅当二者都失效时顶事件发生。设主件x1和备用件x2的发生时间为T1和T2，其概率分布函数分别为G1(x1)和G2(x2)，则顶事件发生时间的概率分布函数GR(t)为

2.2 Monte Carlo仿真法的抽样公式

考虑等式

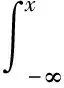
(3)

对x求解即可得分布函数为F(x)的随机变量的一个样本观察值。其中，ξ是由定义在[0,1]区间上的均匀分布u(x)产生的一个随机数(使用计算机产生)[8]。

(1) 对于服从指数分布E(λ)的概率密度函数，若ξ是u(x)产生的一个随机数，则t是E(λ)的一个样本观察值，又因为在[0,1]区间上1-ξ也服从均匀分布，所以表达式可化为

(4)

(2) 对于服从威布尔分布W(t0,m)的概率密度函数，t0与m分别为威布尔分布的尺度参数与形状参数。式(3)的形式为1-e(-tm/t0)=ξ，则抽样公式变为

(5)

3 深海采油树系统动态故障树的定量分析

CHATTERJEE[9]和BIRNBAUM等[10]拓宽了“模块”这一概念的性质并拓展了它在静态故障树中的应用，然后通过基于TARJAN[11]算法的深度优先搜索(Depth-First Left-Most，DFLM)，在动态故障树中查找其中所有的动态子树和静态子树。

通过MATLAB对图 1和图 2所示动态故障树进行两次DFLM。据其遍历结果可见，H4、H11、H12、H22、H23、H24、H37为动态模块，H38、H39为静态模块。

设动态故障树的底事件为X1,X2,…,Xn并进行模块化处理，则完整故障树顶事件概率的解函数f可化为

f=f2(X1,X2,…,Xl,H4,H11,H12,H22,H23,H24,H37,H38,H39)

(6)

分别求解动态模块H4、H11、H12、H22、H23、H24、H37以及静态模块H38、H39的顶事件概率，并将其作为新的动态故障树f2的底事件概率；再对f2求解，即可知动态故障树顶事件概率。

3.1 求解动态故障树顶事件故障概率

3.1.1 求解模块顶事件故障概率

查阅相关数据库[12-14]，可得动态故障树底事件故障率，如表 1所示。

表1 动态故障树底事件故障率 106

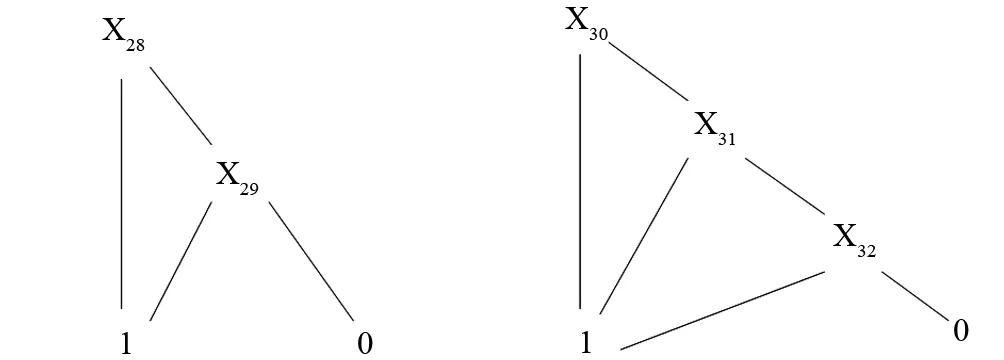
图3 H38、H39模块BDD图

由于X23～X33均为机械电子元件，因此，可设其均服从威布尔分布W(100 000,3)，工作时间为t=104。

动态故障树中H38、H39均为静态模块，可用二元决策图(Binary Decision Diagram， BDD)法求解，其BDD图如图 3所示。

由此可得H38模块的最小割集为{X28}、{X29}，H39模块的最小割集为{X30}、{X31}、{X32}。因此,可得

(7)

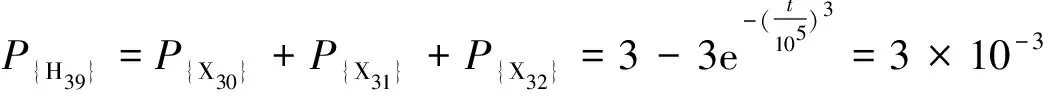
(8)

H22、H23、H24、H37均为动态模块，使用Monte Carlo仿真法进行定量分析求解模块顶事件故障概率。其中，H23、H24模块服从动态逻辑门中的热备件门。由于X23、X24以及X28～X32服从威布尔分布，因此，使用式(5)进行随机抽样。

将产生的随机数代入式(2)，利用MATLAB可实现循环计算过程，可得

P{H23}=7×10-5

P{H24}=1.66×10-3

动态模块中H22、H37服从动态逻辑门中的优先与门。由于X18～X21均服从指数分布，因此使用式(4)进行随机抽样。将产生的随机数代入式(1)可得

P{H22}=2.029 8×10-4

P{H37}=3.720 9×10-4

3.1.2 求解动态故障树最小割集

对于完整的动态故障树，可利用下行法求解其最小割集。(以下以Hi代替PHi，Xi代替PXi)

对于H1模块，由深海采油树系统动态故障树可得

H5=H40·H13=(X1+X2)·(H25+X2)=(X1+X2)·(X1+X2+X3+X2)

=X1+X2+X1·X2+X2·X3+X1·X3

(9)

H6=H14+H15+X6=(H26+X2)+(H26+H27+H28+X4)+X6

=X1+X2+X3+X4+X5+X6+X1·X2+X2·X3+X1·X3

(10)

由式(9)和式(10)，根据布尔运算法则，可得

H1=H5+H6=X1+X2+X3+X4+X5+X6+X1·X2+X2·X3+X1·X3

(11)

对于H2模块，根据布尔运算法则，同理可得

H2=H7+H8=X9+X12+X13+X14+X15+X16+X1·X6+X1·X7+X1·X9+X1·X10+

X2·X6+X2·X7+X2·X9+X2·X10+X10·X11+X1·X8·X9+X2·X8·X9

(12)

对于H3模块，同理有

H3=H9+H10=X9+X10+X12+X13+X14+X15+X16+X17+X22+

H22+H37+X8·X9+X10·X11

(13)

对于H4模块，同理有

H4=H11+H12=H23+H24+X25+X26+X27+X33

(14)

3.1.3 计算顶事件故障概率

深海采油树系统动态故障树的最小割集：

T=H1+H2+H3+H4

(15)

将式(11)～式(14)代入式(15)中可得

p(T)=0.006 3。

(16)

3.2 求解动态故障树基本事件概率重要度和结构重要度系数

概率重要度系数的计算公式[15]为

(17)

式中：p(T)为顶事件发生概率;qi为第i个基本事件发生的概率。

概率重要度的重要性质：设所有基本事件发生概率均为1/2，则结构重要度系数等于此时的概率重要度系数，即

(18)

利用该性质可求解结构重要度系数。

3.2.1 求解基本事件概率重要度

根据式(17)计算一次偏导数，并对基本事件概率重要度排序，如表 2所示。

表2 基本事件概率重要度排序 10-4

由表 2可以看出：基本事件X23～X33在基本事件概率重要度排序中最高，即减小这些基本事件的故障率能迅速减小顶事件的发生概率，而它们都是机械电子元件，因此控制系统需要定期检查、保养，及时更换，并使用高质量的电子元件；基本事件X2、X1在概率重要度排序中紧随电子元件之后，重要度也不可忽视，因此减小人为操作失误和分析失误的概率对减小顶事件发生概率同样十分重要，可以通过聘请高素质人才来设计、操作某些重要部件以减少此类失误。

3.2.2 求解基本事件结构重要度系数

利用概率重要度的性质，可求得其结构重要度系数，如表 3所示。

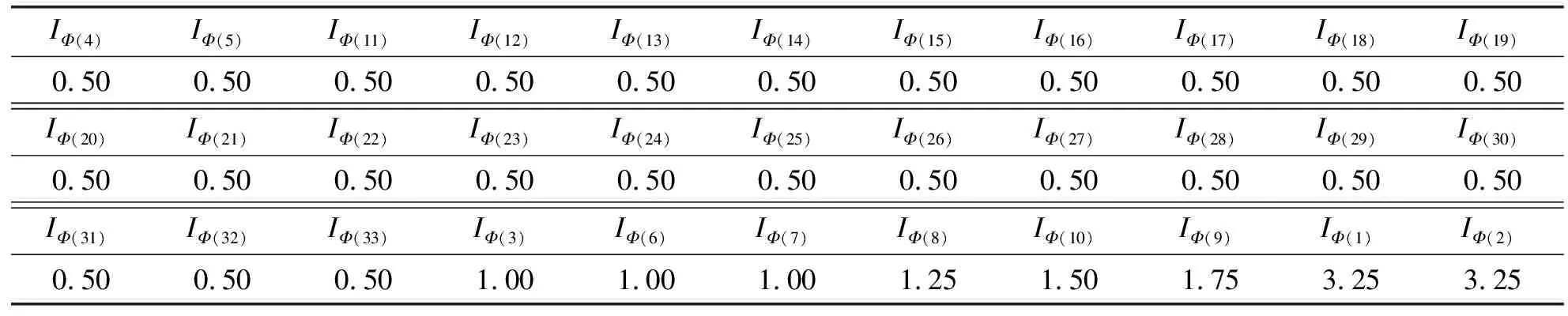
表3 基本事件结构重要度系数排序 10-4

由表 3可知：基本事件X1和X2的结构重要度系数最高，与第3位差距很大，因此减小人为操作失误和分析错误可以规避很多风险，减小顶事件发生概率；基本事件X9、X10、X8的结构重要度系数紧随其后，因此尽量规避易产生较大涡旋和波浪的海域对减小顶事件发生概率有重要作用；基本事件X3、X6、X7的结构重要度系数相同，处于排序表的中间位置，因此避免偶然碰撞、涡激振动以及储运过程中的不利因素同样对减小顶事件发生概率有积极作用。

综上所述，对采油树系统部件进行定期检查、保养，发生故障以后及时更换，或投入较大人力、财力避免人为失误以及减少可控故障，是规避风险的最佳选择。

4 结 语

建立深海采油树系统的动态故障树模型，根据Monte Carlo仿真法对该模型进行了定量分析，计算顶事件故障概率并分析了基本事件的概率重要度和结构重要度系数，最后根据计算结果对采油树系统提出了风险规避的建议。

后续还需继续研究的方面主要有： 深海采油树系统动态故障树模型的底事件发生概率仍然靠经验数据得来，未来可进一步通过调研及试验确定其概率。

现有的Monte Carlo仿真法依旧没有解决状态空间组合爆炸的问题，未来可开发新的算法以使计算更精确。