柔性圆柱涡激振动流体力系数识别方法

(天津大学 a.水利工程仿真与安全国家重点实验室；b.建筑工程学院， 天津 300072)

0 引 言

涡激振动(Vortex-Induced Vibration， VIV)现象普遍存在于桥梁工程、土木工程和海洋工程等诸多领域，是桥梁斜拉索、工厂烟囱、海洋立管等大长径比(长度与直径的比值，L/D)圆柱结构疲劳损伤的重要外界影响因素。近一个世纪以来，VIV一直是备受关注的核心科学问题之一，并取得了大量卓越的研究成果[1-4]。目前，人们对此复杂流-固耦合现象的理解已经上升到了一个全新的高度。

弹性支撑刚性圆柱VIV的流体力特性研究开展较为广泛，常将垂直于来流方向(即横流向)以及平行于来流方向(即顺流向)的流体力合力分解为与速度同相位的力——升力和脉动阻力以及与加速度同相位的力——附加质量力。SARPKAYA[5]试验表明在圆柱横流向VIV“锁定”现象发生时，响应位移与横流向流体力合力的相位角存在跳跃，该现象也被其他学者[6-7]通过数值仿真证实。GOPALKRISHNAN[8]绘制升力系数和附加质量系数云图，发现升力系数与响应频率和响应位移密切相关。VIKESTAD等[9]通过能量转化法分解横流向流体力，获得了附加质量系数，并发现附加质量系数与响应频率相关性强，随约化速度增大而减小，在“锁定”区域变化缓和。ARONSEN[10]研究圆柱顺流向振动的流体力，并运用能量转化法分解得到脉动阻力系数和顺流向附加质量系数。

与弹性支撑刚性圆柱相比，柔性圆柱VIV更复杂：结构振动表现为多模态，模态竞争激烈，在响应中出现高频成分，顺流向振动频率一般近似为横流向的2倍[11-13]。柔性圆柱VIV过程结构振动变形，不同截面处受到的流体力不同。由于测量手段和试验条件的限制，难以在不改变结构外部流场的前提下测量柔性圆柱VIV的流体力分布。SANAATI等[14]测量柔性圆柱VIV总体流体力，研究表明：横流向和顺流向流体力合力在“锁定”区域先增大后减小，在最大位移对应的约化速度处达到最大值。SONI[15]开展模型试验获得柔性圆柱VIV截面处的运动轨迹，并迫使刚性圆柱以上述运动轨迹振动，假定刚性圆柱的水动力系数等价于柔性圆柱截面处的水动力系数，试验发现：顺流向脉动阻力系数和附加质量系数受振动位移的影响较小，横流向附加质量系数出现负值，升力和脉动阻力出现倍频成分。YIN等[16]采用与SONI[15]相似方法识别柔性圆柱VIV的水动力系数，结果表明：若柔性圆柱的振动位移呈现准周期特性，则计算误差较小；若响应位移具有一定随机性，则此方法的不确定性增大。

现阶段柔性圆柱结构VIV的预报主要依靠经验模型，预报结果与模型试验结果存在一定差异[17]，主要原因是经验模型选取的流体力系数来源于刚性圆柱试验。如何准确地识别柔性圆柱VIV流体力一直是工程领域和学术领域共同关注的问题。本文系统地总结现存VIV流体力计算和分解方法，阐述不同方法的计算过程，分析误差来源和适用范围，并对柔性圆柱VIV流体力系数识别方法的进一步完善提出若干合理化建议。

1 VIV流体力计算方法

目前，广泛采用根据结构振动信息逆向求解流体力的方式确定柔性圆柱VIV流体力。工程中的大长径比柔性圆柱结构一般承受轴向预张力，其结构振动控制方程可采用Euler-Bernoulli梁模型，公式可表示为

(1)

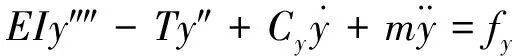
(2)

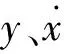
1.1 一般有限元法

柔性圆柱结构可离散为若干个单元，每个单元包含2个节点，共计4个自由度。结合圆柱结构两端边界条件，柔性圆柱振动的有限元方程形式为

(3)

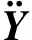
C=αM+β(KE+KG)

(4)

式中：α和β为常系数，通过柔性圆柱在空气中的自由衰减试验测得。根据获取的流体载荷矩阵Fy，确定柔性圆柱各节点处流体力合力fy。HUERA-HUARTE等[18]采用有限元法计算阶梯来流下柔性圆柱VIV的流体力，并计算相应的流体力系数。有限元法求解的阻力系数与测量值对比如图1所示，计算结果与试验结果吻合较好。图1中横坐标为约化速度Vr(Vr=U/f1D, 其中U为来流速度，D为结构外径，f1为结构静水中一阶固有频率)，纵坐标为平均阻力系数Cd(Cd=2Fd/(ρDLU2), 其中Fd为结构顺流向的平均阻力，ρ为外部流体密度，L为结构长度)。WU[19]采用有限元法计算流体力并与VIV预报软件VIVANA的结果进行对比，发现两种方法均可取得精度较好的计算结果。有限元法发展较成熟且稳定可靠，是目前广泛应用的方法。除均质性等材料本身性质所造成的误差之外，误差的主要来源是计算过程中刚度、质量、阻尼矩阵不会随着时间变化而更新[18]，此外还受计算的空间分辨率即网格划分的精细程度的影响。

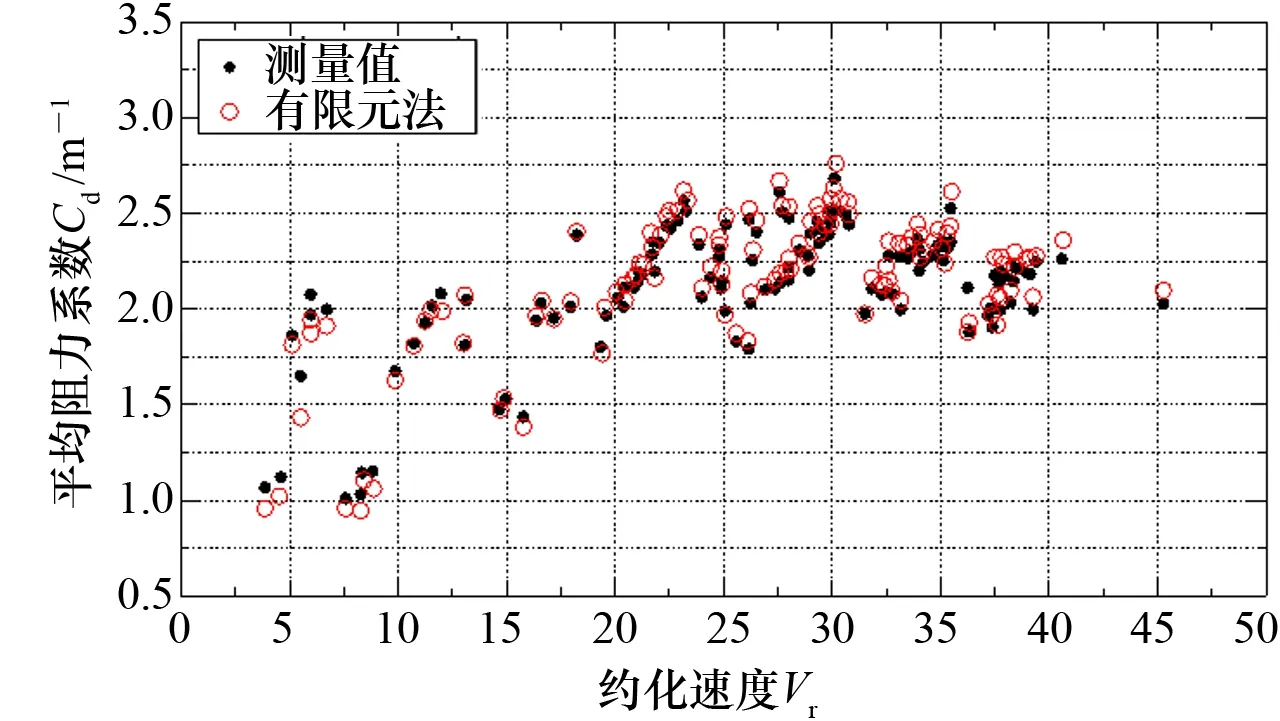
图1 有限元法求解的阻力系数与测量值对比

1.2 凝聚自由度有限元法

此方法基于有限元计算模型，将一般有限元方程中结构转角自由度凝聚。对于具有n个平动自由度和s个转动自由度的系统，可通过矩阵H*转换为仅有n个平动自由度的系统。

唐国强[20]阐述凝聚自由度的有限元法，识别立管VIV的流体力系数。LI等[21]采用此方法识别海底悬跨管道VIV流体力系数。通过模态分解法可将由柔性圆柱VIV试验获得的应变信息转化为位移，但转角未计算求得。在凝聚自由度有限元法应用过程中，可省去计算转角的步骤，但凝聚自由度的过程存在一定误差，当结构单元质量较大即结构惯性力较大时，此法的精度较差。当结构振动频率较高时，凝聚自由度法也会引入较大的误差。此方法仅在结构单元质量较小、振动频率较低时才更合理适用[22-23]。

1.3 基于广义积分变换的反解法(GITT)

结合两端边界条件，根据广义积分变换法，柔性圆柱结构横流向振动频率即特征值求解方程为

(5)

式中：λi为特征值；φi(z)为振型函数，i为第i阶模态阶次。根据特征方程的正交准则和式(6)

(6)

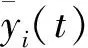
(7)

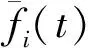
(8)

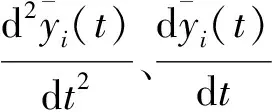
GU等[24]采用广义积分法计算柔性圆柱VIV流体力，计算结果与HUERA-HURATE等[18]的有限元法结果对比如图2所示，结果吻合较好，进一步表明广义积分法对柔性圆柱VIV流体力的识别具有可行性。在图2中，T1为HUERA-HURATE等的计算数据，T2为GU等的计算数据。该方法应用还不甚广泛，对其适用条件和误差来源等有待进一步研究[24]。

图2 GITT法与有限元法求解的顺流向阻力系数对比

1.4 基于卡尔曼滤波的反解法

式(3)采用状态空间方程表示为

(9)

式中：W为系统状态向量；Λ为系统输出向量；A、B、G分别为具有一定维数的系统矩阵。

考虑测量噪声v(t)和过程噪声w(t)的影响，离散状态空间平衡方程为

(10)

其中

(11)

式中：k为离散的时间步长；τ为时间。测量噪声v(t)和过程噪声w(t)的方差用R和Q表示。R和Q需在计算结构VIV流体力前计算获得，在试验中测量噪声方差R较易确定，但过程噪声方差Q的计算较困难，可通过数值模拟确定。具体的流体力计算过程见文献[19]。

在流体力计算中引入遗忘因子。遗忘因子的作用是加强当前数据的影响并削弱历史数据的影响，消除数据饱和现象。若遗忘因子等于1.0，则为基本最小二乘法，此时历史数据的影响较强，噪声的影响减弱。若遗忘因子较小，则为递推最小二乘法，当前数据的影响较强，计算收敛的速度较快。需权衡计算精度与计算效率选择合理的遗忘因子。

上述方法基于卡尔曼滤波，核心思想是用前一步的历史信息计算当前时刻的流体力。MA等[25]最早将基于卡尔曼滤波的反解法用于悬臂梁结构的输入力识别，并通过与其他数值模拟法的对比验证该方法的准确性。WU[19]亦运用该方法识别柔性圆柱VIV流体力。在采用此法计算结构流体力时，流体力与结构响应位移、响应加速度之间存在不确定的时间延迟[19,25]。在流体力系数计算过程中需考虑流体力与响应位移之间的相位差。结构流体力计算时间延迟会在确定流体力系数时引入一定的误差[19]。此外过程噪声方差Q和测量噪声方差R较大也会使测量结果产生误差，但先进测量方法已可将其控制在较低水平，在一定程度上保证反解的准确性[25]。

1.5 基于最优控制理论的反解法

基于最优控制理论的反解法主要通过使状态向量W与输出向量Λ无限接近，从而计算出结构的流体力。此法本质上是一种优化算法，即得到误差最小的最优解。

假设向量Λ服从期望值为Λ0、标准差为σΛ的高斯分布。目标函数可表示为

(12)

式中：QΛΛ为输出向量的协方差矩阵；σΛ为标准差；I为单位矩阵。结构流体力的目标函数为

(13)

式中：QFyFy为结构流体力的协方差矩阵；σFy为计算得到的流体力与真实流体力之间误差的标准差。结合两个目标函数，基于最优控制理论即可计算流体力[19]。

上述方法的计算结果受QΛΛ和QFyFy的影响较大。若QΛΛ较大，计算出的响应位移与测量结果相关性强，计算结果受测量误差的影响较大，造成结果的方差较大。若QFyFy较大，计算结果与测量结果的相关性弱，造成结果的偏差较大。若测量的数据准确性较高，QΛΛ和QFyFy将处于相对稳定的范围，计算结果的方差和偏差均较小[19]。

WU[19]将该方法识别的柔性圆柱VIV流体力的结果与利用VIVANA模型和有限元法计算结果进行对比，在低模态和高模态取较多测点的情况下，结果的相似性较好。如果在高模态下测点较少，结果会产生一定的误差。该方法的主要难点在于数值计算，自身属性不好的矩阵易在计算过程中出现不稳定的问题。此外，上述方法的计算时间与自由度的四次方成正比，若自由度较大，应用上述方法较为困难。在高模态下的计算准确度仍有待验证[26]。采用凝聚自由度的方法将柔性圆柱结构的转动自由度凝聚，能显著改善数值计算条件[19]。

1.6 基于振动方程的直接反解法

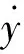
SONG等[27]采用上述方法计算柔性圆柱结构的流体力，并通过ABAQUS有限元计算软件检验上述方法的计算精度。首先对柔性圆柱结构施加已知载荷，运用ABAQUS求解结构的振动响应，根据振动响应采用直接反解法计算柔性圆柱结构受到的载荷，比较计算获得载荷与施加载荷的差异。该方法的准确程度直接取决于测点位移的精确程度，其计算精度亦受试验测点个数的影响。若测点个数大于等于柔性圆柱结构实际激发的模态数，直接反解法的计算精度较高；若测点个数小于柔性圆柱结构实际激发的模态数，由直接反解法计算得到的结构流体力与结构实际受力差异较大，计算精度较低。

2 流体力分解方法

以升力系数和横流向附加质量系数的计算方法为例介绍流体力分解的方法，脉动阻力系数和顺流向附加质量系数的计算方法与之类似，不再赘述。在柔性圆柱VIV过程中结构实际受到的流体力可表示为三角函数形式，并分解为与速度同相位的力和与加速度同相位的力，公式为

fy=f0sin(ωt+φ)=f0cosφsin(ωt)+f0sinφcos(ωt)

(14)

式中：ω为横流向的振动圆频率；φ为横流向流体力与振动位移相位差；f0为横流向流体力幅值。

2.1 最小二乘法

柔性圆柱VIV横流向流体力合力的真实值可用升力系数CL和横流向附加质量系数Cay表示为

(15)

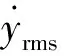
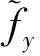
(16)

通过最小二乘拟合使计算值与真实值的差最小，得到升力系数和横流向附加质量系数的计算公式为

(17)

其中

ARONSEN[10]介绍最小二乘法分解刚性圆柱的流体力合力。SONG等[27]根据直接反解法确定结构流体力，采用最小二乘法获得柔性圆柱VIV的升力系数、脉动阻力系数和附加质量系数。最小二乘法是一种偏数值方法，在流体力分解过程中不涉及数值积分，通过Matlab等数学软件采用最小二乘拟合的方式，计算得到与真实水动力系数误差最小的升力系数和附加质量系数。

2.2 能量转化法

在柔性圆柱VIV过程中转移能量的平均值可表示为

(18)

振动位移可表示y(t)=y0sin(ωyt)，能量转移的平均值可表示为

(19)

由式(18)和式(19)可得

(20)

通过相同的推导方式计算与加速度同相位的项为

(21)

升力系数、横流向附加质量系数计算式为

(22)

能量转化法是刚性圆柱流体力分解应用较多的方法。ARONSEN[10]用该法分解刚性圆柱纯顺流向流体力。VIKESTAD等[9]用能量转化法获得刚性圆柱结构的附加质量系数，并与GOPALKRISHNAN[8]的结果进行对比，结果吻合良好。TANG等[28]和WU[19]根据能量转化法分解柔性圆柱流体力合力，与模型计算对比，结果亦比较准确。

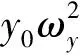
2.3 傅里叶平均法

傅里叶平均法是根据傅里叶变换的基本理论对流体力进行分解的方法。将计算得到的流体力fy乘以cos(ωt)，在n个振动周期(TOSC)内积分，可得与速度同相位的力为

(23)

将计算得到的流体力fy乘以sin(ωt)，在n个振动周期内积分，可得与加速度同相位的力为

(24)

GOPALKRISHNAN[8]采用傅里叶平均法分解刚性圆柱横流向流体力合力得到升力系数和附加质量系数。傅里叶平均法在流体力分解过程中仅使用流体力信息，误差主要来源于式(23)和式(24)的数值积分过程。

2.4 传递函数法

传递函数法为频域方法，假定输入函数(结构VIV的频率和位移)与输出函数(结构VIV的流体力)之间为线性关系。振动位移与流体力的相关函数H(ω)应为位移、流体力的互功谱S(ω)与位移自功谱Syy(ω)的比值，即

(25)

当已知振动位移的幅值y0时，f0和φ的计算式为

(26)

然后求出与速度同相位的力f0sinφ和与加速度同相位的力f0cosφ，ARONSEN[10]提出传递函数法用于刚性圆柱流体力合力分解。传递函数法的误差相对较大，传递函数法在频域内进行计算，误差主要来源于频率分辨率，计算的结果相对比较保守。

3 结论与展望

根据结构响应逆向求解结构受力是识别柔性圆柱VIV流体力的常用方法。分析对比多种流体力计算方法，总结归纳了不同方法的适用范围和误差来源。研究发现：有限元法是较为传统、成熟的一般方法，在柔性圆柱结构VIV流体力计算方面应用广泛，即使因采用的矩阵在计算过程中不随时间步长更新而产生一定误差，总体计算结果仍相对稳定[18]。凝聚自由度法在计算结构流体力过程中虽可降低结构自由度数目，提高计算效率，简化计算步骤，但对于单元质量较大、响应频率较高的结构，凝聚自由度法将引入较大误差[22-23]。基于卡尔曼滤波和最小二乘法的反解法在计算流体力时，采用前一时刻响应位移计算下一时刻流体力，存在不确定的时间延迟，在后续流体力分解过程中将引入不确定的误差[19]。基于最优控制理论的反解法在数值计算过程中存在难点，对数据要求较高，质量较差的数据易引起计算不稳定的问题[19]；计算周期较长，计算时间与自由度数目的四次方成正比，受自由度数目的限制，虽然能通过凝聚自由度来提高计算效率，但凝聚自由度方法的应用会引入新的误差。直接反解法和广义积分变换法在计算柔性结构VIV流体力方面具有可行性，但应用并不广泛，其稳定性需进一步检验[24]。

为了深入研究柔性圆柱VIV流体力特性，通常将流体力合力分解为与速度同相位分量和与加速度同相位分量。流体力的分解方法亦有多种：频域上的传递函数法误差相对较大[10]，最小二乘法和能量转移法应用较为广泛，其精确度与计算过程的积分计算关系较大[9-10,27]。应用能量转移法、傅里叶平均法以及最小二乘法的基本前提是VIV位移和流体力的时域信号应近似为简谐形式，时域信号越接近简谐形式，误差越小。

为了提高识别精度和结果的可靠性，未来关于圆柱VIV流体力系数识别的研究可着眼于以下几方面：

(1) 目前的流体力计算方法仅考虑单个频率，柔性圆柱VIV多个模态共存，响应频率存在倍频成分，其影响有待深入研究。应建立包含多频成分的流体力计算模型，更全面获取圆柱VIV流体力信息。

(2) 现有方法大多将模型试验的应变信息转化为位移，通过位移求解结构的受力，这一过程存在不可避免的误差。为提高计算精度，可改进计算方法，直接通过结构应变信息识别结构受力。

(3) 改进目前试验测量手段，通过传感器直接测量得到柔性圆柱VIV流体力分布，将大幅降低流体力识别误差。