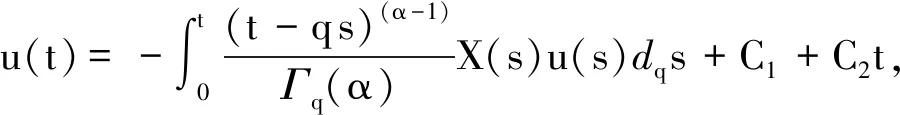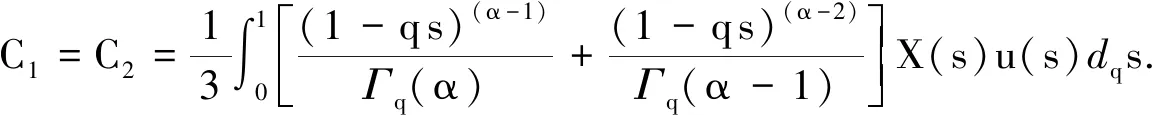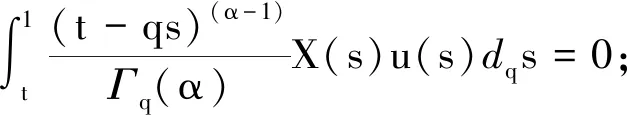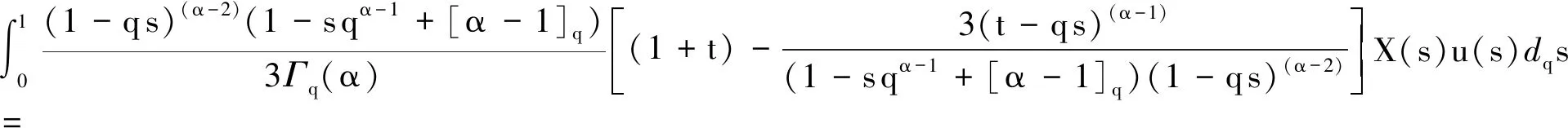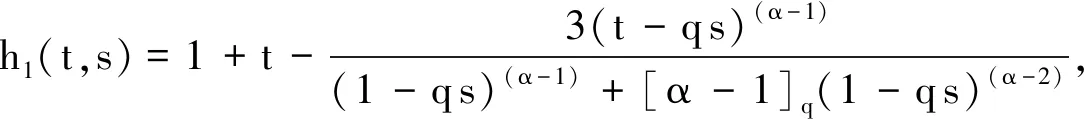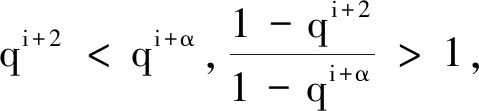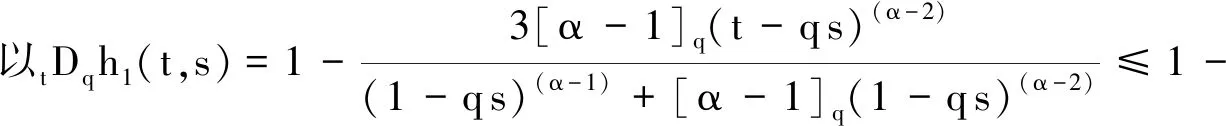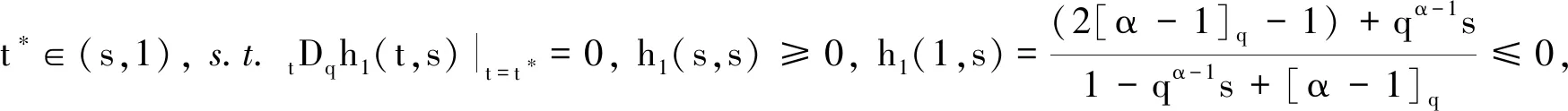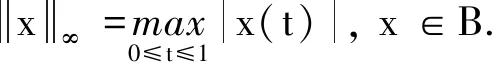带有Robin边界条件的分数阶q -差分方程的Lyapunov型不等式
陈祉睿, 侯成敏
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
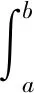
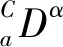
(*)
这里1<α≤2,q∈[0,1),f∶[0,1]→R是连续函数.
1 预备知识
定义1[4]f在[a,b]上连续,q∈[0,1), 定义f(t)一阶q-差分为

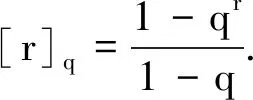
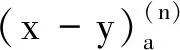
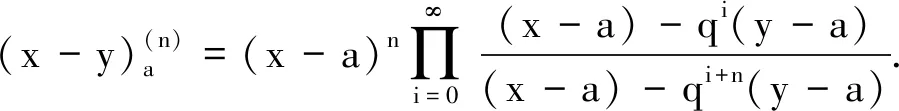
性质1对于任意的t,s∈[a,b], 下列等式成立:
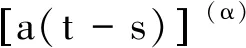
引理1已知f在[a,b]上连续,假设对于任意的q∈[0,1), 有aDqf(t)≤0 (aDqf(t)≥0),a 由此得出f(y)≤f(x),引理1得证. 引理2[7]f和g是[a,b]上的连续函数,则: 为方便引入如下记号: h2(t,s)=1+t. (1) (2) (3) 因此 引理5得证. 引理6对于任意的(t,s)∈[0,1]×(0,1), 下式成立: (4) 证明1)显然,当0≤t≤s≤1时,有0≤h2(t,s)≤2. 下面证明[tDqh1(t,s)]t→s+<0, 即: (1-qs)(α-1)+[α-1]q(1-qs)(α-2)<3[α-1]q(s-qs)(α-2), (1-qs)(α-1)<3[α-1]qsα-2(1-q)(α-2)-[α-1]q(1-qs)(α-2). (5) 因为(1-qs)(α-1)关于s递减,故有(1-q)(α-1)≤(1-qs)(α-1)≤1.又因为(1-qs)(α-2)关于s递增,故有1≤(1-qs)(α-2)≤(1-q)(α-2).若使式(5)成立,只要满足下式即可: 1<3[α-1]qsα-2(1-q)(α-2)-[α-1]q(1-q)(α-2). 又因为sα-2关于s递增,故有sα-2≥1.因此,若使式(5)成立,需满足下式: 1<3[α-1]q(1-q)(α-2)-[α-1]q(1-q)(α-2)=2[α-1]q(1-q)(α-2)= 固定区间(0,1)上的点s. 当t∈[s,1]时,有 令a*=(1-2[α-1]q)q1-α, 以下分两种情况讨论. (Ⅰ)如果a*≤0, 则1-2[α-1]q≤0 ⟺ 1+q-2qα-1≥0且 (Ⅱ)如果0 i)若a*≤s<1, 有1-2[α-1]q≤qα-1s, 且 同理,可以得出h1(1,s)≤h1(t,s)≤h1(s,s)≤2.由1-2[α-1]q≤qα-1s得 2(1-qα-1s+[α-1]q)-3(1-qα-1s)=qα-1s-(1-2[α-1]q)≥qα-1s-qα-1s=0, 即h1(1,s)≥0.因此0≤h1(t,s)≤2. ii)若0 |h1(t*,s)|≤max{-h1(t*,s),2}. (6) 观察tDqh1(t,s)|t=t*=0 ⟺ 3[α-1]q(t*-qs)(α-2)=(1-qs)(α-1)+[α-1]q(1-qs)(α-2),可知 定理1如果方程(*)有一个非平凡的连续解,那么

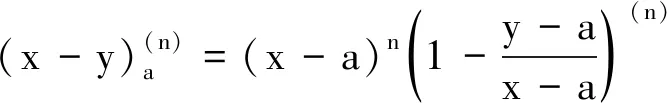


2 主要结果及其证明