基于神经网络自适应动态逆的结冰飞机飞行安全边界保护方法
魏扬,徐浩军,薛源,*,郑无计,李哲,裴彬彬
1. 空军工程大学 航空工程学院,西安 710038 2.空军石家庄飞行学院 第四训练旅,保定 074212
飞机在正常飞行过程中,飞行速度、迎角、滚转角等飞行参数存在着一个安全范围,该范围的边界值称之为飞行安全边界。结冰引起飞机气动性能恶化通常会导致飞行边界的萎缩。如果驾驶员或者自动驾驶仪仍在原有未结冰的飞行边界内操纵飞机,发生飞行风险的概率就会大大增加。因此开展结冰情形下的边界保护方法研究,对于保障结冰情形下的飞行安全,具有重要的意义。
在飞机结冰后飞行安全边界保护研究方面,国外的Bragg等开发了智能结冰系统(SIS)[1-2],可实时、直接地测量飞机结冰对飞行性能及操稳特性的影响程度,并适当调整控制律,进行飞行边界保护;Sharma和Voulgaris提出了自动驾驶仪模式下的结冰边界保护方法[3],探讨了如何将迎角维持在随结冰不断变化的失速范围之内;Merret等[4]则研究在大气扰动下飞机结冰时如何实现飞行包线保护的问题;Hossain等[5]利用自适应控制技术,对飞机遭遇结冰后的开环和闭环包线保护算法进行了研究;Gingras等[6]设计出结冰包线保护系统,通过将先验信息和实时气动数据估计值结合起来确定出飞行包线,并向驾驶员提供安全飞行包线提示;美国田纳西大学与Bihrle研究公司联合开发了积冰污染边界保护系统(Icing Contamination Envelope Protection,ICEPro)[7-9],提出了结冰边界告警与保护方法。文献[10-12]针对飞行安全边界保护算法进行了研究,为结冰情形下的边界保护提供了参考思路。
在国内,南京航空航天大学团队采用结冰影响工程计算模型,对结冰的飞行动力学特性与包线保护控制律进行了分析[13];复旦大学团队研究了结冰飞行气动参数的辨识方法与飞机闭环结冰边界保护方法[14-15];空军工程大学团队提出了结冰条件下的最优迎角边界保护方法[16],通过相平面法[17]和流形理论[18]构建了结冰飞机的稳定域,为结冰后飞机安全飞行边界的确定及保护提供了理论参考。
在上述研究中,大多仅对迎角单个参数进行边界保护,同时在建模过程中没有考虑因测量误差或外界干扰引起气动参数摄动情况下控制的鲁棒性问题。在进行结冰边界保护时,需要提前设置好先验信息,如不同结冰状态下离线的数据库(如可用迎角、俯仰角等),实时性相对较差。
为此,本文基于神经网络自适应动态逆跟踪性能好、无超调、鲁棒性强的优点,提出了一种基于神经网络自适应动态逆的边界保护方法。对于结冰后气动参数获取不准确、外界扰动或是传感器误差导致的不确定性逆误差采用单隐层神经网络进行在线自适应补偿,能够有效降低动态逆对模型准确性的要求,增强了控制系统的鲁棒性。所提出的结冰边界保护系统,能够保证飞机在容冰飞行情形下的飞行安全,具有一定的工程应用价值。
1 模型的建立
1.1 飞机结冰气动数据库
目前,常用于飞行仿真中的飞机结冰气动模型主要采用Bragg教授提出的一种结冰参量模型[19],该模型是基于双水獭(DHC-6)飞机的结冰飞行试验数据拟合分析得到的。该模型采用结冰严重程度因子评估结冰对气动性能的影响,该因子依据飞行气象条件及飞行状态,通常采用气动参数辨识的方法确定,但精度不够高,无法直接移植到其他气动布局差异较大的飞机上来估算结冰的气动影响。
本文采用数值模拟方法获取飞机结冰气动参数。图1为背景飞机结冰气动数据的获取流程。首先构建了背景飞机的几何模型,建立了干净构型的三维数模。考虑到角状冰对飞机气动特性影响最大,以角状冰为例根据可靠的结冰冰形实验数据形成了典型结冰环境下机翼重度和中度角状冰模型,如图2所示。采用高精度数值模拟方法计算了典型状态下机翼结冰对飞机气动参数的影响。最终通过风洞虚拟试飞验证,获得了一套可靠的飞机结冰后纵向及横航向的气动参数数据库。
图3~图5为3种不同状态下(干净构型Clean、中度结冰构型Ice-B、重度结冰构型Ice-A),马赫数Ma=0.4时的升力系数CL、阻力系数CD与俯仰力矩系数Cm随迎角α的变化曲线。

图1 背景飞机结冰气动数据的获取流程Fig.1 Acquisition process of icing aerodynamic data of background aircraft

图2 重度结冰和中度结冰几何模型对比及空间位置关系Fig.2 Comparison of heavy and moderate icing geometric models and spatial positional relationship

图3 升力系数变化曲线Fig.3 Curves of lift coefficients change

图4 阻力系数变化曲线Fig.4 Curves of drag coefficients change

图5 俯仰力矩系数变化曲线Fig.5 Curves of pitching moment coefficients change
图3~图5的结果显示,干净构型、中度结冰和重度结冰状态下,升力线斜率和最大升力系数依次下降,失速迎角依次减小,最小阻力依次增加,纵向静稳定裕度依次降低。
1.2 飞机动力学模型
1.2.1 飞机本体模型
飞机本体六自由度全量的非线性动力学模型可以用向量形式表示为[20-22]

(1)
式中:x为状态向量,
(2)
其中:V、α和β分别为飞行速度、飞机迎角与侧滑角;xg、yg、zg为飞机在地面坐标系下的位置。
u为控制向量,
(3)
其中:δth为飞机油门偏度;δe、δa、δr分别升降舵、副翼以及方向舵舵面的偏角。
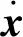
(4)
(5)
(6)
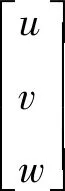
(7)

(8)
1.2.2 舵机模型
舵机模型可简化为由一阶惯性环节、速率限制器和舵偏位置限制器构成[23],如图6所示。图中:T为一阶惯性环节的时间常数;1/(Ts+1)为舵机的传递函数。
舵机速率限制器以及舵偏位置限制器的具体参数可参考文献[24]中的有关参数进行设置。

图6 舵机动力学模型示意图Fig.6 Schematic diagram of dynamics model for actuator
2 现有的结冰边界保护系统工作原理
现有的结冰后边界保护问题研究[4-5]总体来说,主要从开环边界保护(驾驶员人工操纵)与闭环边界保护(自驾仪模式)两个方面展开。开环边界保护的核心思想是:通过预测关键飞行参数矢量yp是否满足式(9)来判断是否应当采取保护措施。
(9)

根据结冰飞机飞行动力学的描述,飞行参数是飞机状态矢量、控制矢量与结冰严重程度参数η(干净构型、中度结冰与重度结冰)的函数,即
yp=f(x,u,η)
(10)
开环边界保护的方法是通过在飞行过程中对飞机运动方程积分来预测安全关键飞行参数矢量变化是否会超出其结冰后的边界值。一旦式(9)的条件不满足,边界保护系统会通过迭代,计算出舵面的允许最大偏转角,并修正舵面偏角使飞机保持在安全边界内飞行。闭环结冰边界保护系统主要面向自驾仪工作的情形,其设计目标是:在确保飞行安全的前提下,尽可能地完成驾驶员预设的工作指令。
以飞机在自驾仪俯仰姿态保持(Pitch Altitude Hold, PAH)模式下运行为例,其工作原理框图如图7[3]所示。根据图中所示原理,“极限值计算”模块基于飞机状态参数、结冰严重程度计算关键参数的极限值;“允许指令值计算模块”以过失速迎角、结冰严重程度参数η、飞机状态参数作为输入来得到当前状态下的最大允许指令俯仰角,从而能够在驾驶员给定的指令俯仰角过高进而可能会导致迎角超限的情况下,飞行控制系统自动减小指令俯仰角的值,来确保自驾仪在PAH模式下的飞行安全。对于闭环边界保护而言,为了获取飞机在不同结冰程度、不同飞行状态下可用指令俯仰角,需要开展大量的仿真或频域分析等工作,这是相当耗时耗力的。
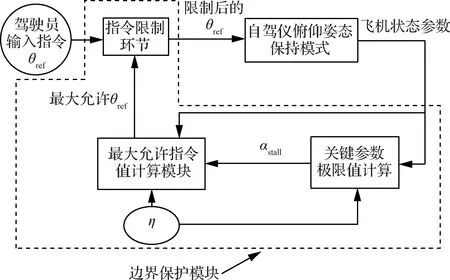
图7 闭环边界保护系统工作框图[3]Fig.7 Block diagram of closed loop envelope protection system[3]
3 结冰边界保护系统设计
3.1 神经网络自适应动态逆控制框架
非线性动态逆(Nonlinear Dynamic Inversion, NDI)控制是一种具有零超调、跟随性较好的控制方式,但动态逆对模型的误差较为敏感,使得该方法应用受到一定的限制。为此本文采用神经网络自适应动态逆方法设计控制律,对于结冰后气动参数获取不准确、外界扰动或是传感器误差导致的不确定性逆误差采用单隐层神经网络(Single Hidden Layer Neural Network,SHL-NN)进行在线自适应补偿,能够有效降低动态逆对模型准确性的要求,增强控制系统的鲁棒性。图8为基于神经网络的自适应逆控制的原理框架。

图8 神经网络自适应动态逆控制框架图Fig.8 Block diagram of adaptive neural network dynamic inversion control
3.1.1 神经网络自适应动态逆控制律设计方法
对于一个一阶的仿射非线性系统:

(11)
式中:x∈R1为状态变量;u∈R1为输入向量;f(x)、g(x)均为非线性映射函数。
基于动态逆的思想,对于式(11)描述的系统进行求逆运算,选取合适的控制量输入u,使得
u=g(x)-1[v-f(x)]
(12)
从而获得期望的动态响应:

(13)
则原系统被补偿为线性系统,v被称为伪控制变量。
由于外界干扰、气动参数获取不准确的影响,同时在求取系统的逆模型时进行的是近似计算,将不可避免地存在参数摄动和建模误差。引入逆误差,式(13)将变为
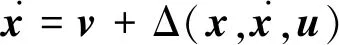
(14)
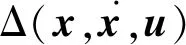
为了消除逆误差的影响,本文在控制器中增加由神经网络构成的自适应环节,将其输出信号叠加到伪控制量中,以消除逆误差的影响。伪控制量由指令滤波器、线性控制器和神经网络输出信号3部分叠加构成:
v=vf+vl-vad
(15)
式中:vf为指令滤波器的输出伪控制信号。当输入指令为xc时,指令滤波器的输出信号为xf,vf可表示为
(16)
vl为线性控制器输出的伪控制信号:
(17)
vad为神经网络输出伪控制信号,将式(15)~式(17)代入式(14),误差动态特性写为
(18)

需要选择合适的kp、kd使得系统矩阵A成为Hurwitz矩阵。由式(18)可知,在理想情况下,神经网络自适应环节的输出项如果能够完全补偿逆误差,则系统的跟踪误差将渐进趋于零。
3.1.2 单隐层神经网络构造
单隐层神经网络已经被证明具有良好的非线性逼近特性[25]。本文采用的单隐层神经网络结构如图9所示。
该神经网络的输入输出关系可表示为
i=1,2,…,n3
(19)
式中:σ(·)表示隐含层激励函数;vkj表示输入层到隐含层的连接权值;wji表示隐含层到输出层间的连接权值;θvj、θwi表示神经网络的偏置项,本文中均取为1;n1、n2、n3分别表示输入层、隐含层和输出层神经元的个数。
若定义x=[1x1…xn1]T,y=[y1y2…yn3]T,σ(z)=[1σ1(z1) …σn2(zn2)]T。V∈R(n1+1)×n2为输入层到隐含层的连接权值矩阵,W∈R(n2+1)×n3为隐含层到输出层间的连接权值矩阵。由此可将单隐层神经网络输入与输出写成如下的矩阵形式:
y=WTσ(VTx)
(20)
式中:

图9 单隐层神经网络结构Fig.9 Structure of single hidden layer neural network

隐含层神经元激励函数选择如下的S型函数:
(21)
式中:z∈R;a为激励系数。
(22)
式中:ε为误差函数的重构误差;V*、W*为神经网络重构逆误差的理想权值。通常理想的神经网络权值矩阵无法直接解析计算得到,但可基于李亚普诺夫稳定性理论,通过设计权值更新的自适应律,在线调整神经网络权值(包括神经元阈值),使之以较高的精度逼近理想的权值矩阵。
定义自适应项vad为
(23)

则系统的跟踪误差动态方程可以写为
(24)
定义矩阵
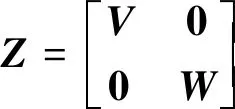
(25)
并引入假设:
假设1系统中所有指令信号均有界。
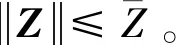
这里定义神经网络的输入为
(26)
设计鲁棒项vr为
(27)
式中:kr0≥0;kr1>0;r=eTPB,P为李亚普诺夫方程ATP+PA=-Q的正定解,这里取Q=2I,I为单位矩阵。
设计权值更新的自适应律为
(28)
(29)
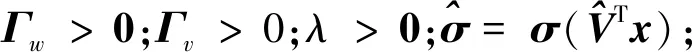
在该权值调整规则的作用下,对于式(11)所描述的仿射非线性系统,采用图8所示的神经网络动态逆控制器,控制结构解析表达式为式(15),自适应补偿项为式(23),并且满足上述假设,可以保证闭环系统内所有信号有界,只要控制参数设置正确,误差将收敛到零的较小邻域内。具体的稳定性证明过程可参考文献[26],限于篇幅这里不再赘述。
3.2 基于神经网络自适应动态逆的飞行控制律设计
对于常规构型的飞机而言,系统的控制输入维数一般小于系统的状态变量维数,不能直接用动态逆的方法进行求解。在实际的飞控系统设计过程中,解决的方法是根据奇异摄动原理,以时间为尺度,按照飞机状态变量变化快慢程度将系统划分为快回路与慢回路两个回路分开进行控制,然后分别针对两个回路进行动态逆控制器的设计。其结构如图10所示。
这里在慢回路中设计3个神经网络自适应补偿器,分别对飞机俯仰、滚转和偏航控制通道逆误差进行自适应补偿,以增强控制系统的稳定性。选择在慢回路增加神经网络补偿,是因为:① 在机动飞行期间,驾驶员主要控制量为慢状态变量,而慢回路采用近似求逆设计,将产生一定的逆误差;② 慢回路作为控制系统的外回路,内回路所产生的逆误差也会传递到外回路中。
快回路实现对飞机的角速率参数p、q、r进行控制,其输出为飞机的舵面偏转角δe、δa、δr;慢回路实现对飞机的气流角β、α、μ控制,其输出参数为飞机角速率指令信号pc、qc、rc传递给快回路作为输入。
1) 快回路控制律设计
对内环快回路控制律进行设计时,首先应当将快变量p、q、r对应的动力学方程转化为仿射方程的形式:
(30)
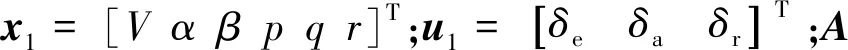
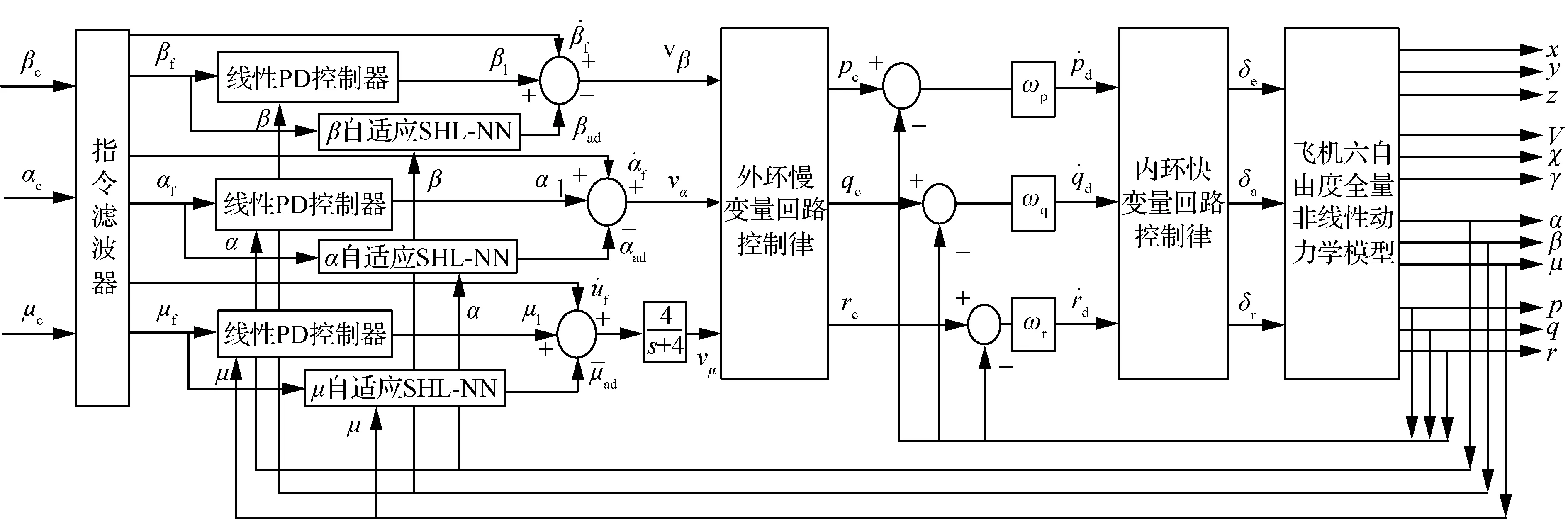
图10 基于神经网络自适应动态逆的飞行控制律设计框图Fig.10 Design block diagram of flight control law based on adaptive neural network dynamic inversion

(31)
f(x1)的表达式为
(32)
对于非线性动态逆控制而言,期望的快回路动态响应可设定为
(33)
式中:下标d表示期望值;ωp、ωq、ωr为带宽,其取值依据是既不会激发舵机执行机构的结构模态又能够满足其带宽的限制,这里设定为10 rad/s。根据动态逆理论,为达到期望的角速率,飞机的内环控制律为
(34)
2) 慢回路控制律设计
飞机的外环回路控制律的作用是为了实现飞机对驾驶员输入指令βc、αc、μc的跟踪,根据这3个 参数对应的动力学方程,可得到
(35)
式中:xs1=[βαμ]T为由慢状态变量构成的向量,f(xs1)与G(xs1)的表达式分别为

(37)
其中:T为推力;Y为侧力;L为升力;G为重力。Tx、Ty、Tz为推力在风轴系的3个分量,Gya、Gza为重力在风轴系y方向和z方向上的分量。G′(xs2)是与控制变量δe、δa、δr有关的项,对于外环控制回路而言,慢状态变量参数在很大程度上依赖于快状态变量参数p、q、r的变化,而控制变量对其影响则相对较小,为简化计算,一般将其忽略。
对于飞机外环控制律而言,将其指令参数的期望动态响应设定为
(38)
根据动态逆理论,忽略式(35)中的舵面控制项G′(xs2),通过解算,可得飞机的外环控制器的输出为
(39)
3.3 结冰边界保护系统设计
如图11所示,为自驾仪俯仰姿态保持模式下的结冰闭环边界保护系统工作框图。同理,在自驾仪滚转角保持、航向角保持模式下的结冰闭环边界保护系统可类似设计。这里以迎角和飞行速度为结冰飞行的关键安全参数进行边界保护。

图11 神经网络自适应动态逆闭环边界保护系统工作框图Fig.11 Block diagram of closed loop envelope protection system based on adaptive neural network dynamic inversion
基于神经网络自适应动态逆结冰边界保护系统具体的工作流程为
1) “飞行参数限制”模块根据当前结冰严重程度和飞行状态插值计算出结冰后的失速迎角。
2) “神经网络自适应动态逆环节”模块根据“飞行参数限制”模块计算出的失速迎角得到可用升降舵的值。
3) “舵面限制器”模块通过对比自驾仪的升降舵输出值与步骤2)中得到的可用升降舵的值来确定最终的升降舵偏转量。在正常状态下,飞机的舵面偏转量等于自驾仪的输出值;一旦自驾仪计算出来的舵面输出量超出了动态逆环节计算出来的结果,飞机的实际舵面输出则等于动态逆环节的舵面输出。考虑到误差及噪声的影响,直接用失速迎角的值来计算可用升降舵偏转角可能会使得飞机进入危险的境地,为此这里采用αstall-Δ作为动态逆环节的输入。Δ代表失速迎角的安全裕量。Δ取值过大将会形成过度保护,影响飞机性能的发挥,本文中Δ的取值设定为0.5°。
上述基于神经网络自适应动态逆环节的结冰边界保护可实现对迎角进行实时限制,此外,考虑到飞行过程中结冰会降低飞机最低平飞速度,一旦驾驶员没有注意到飞行速度接近结冰后的失速速度,极有可能会引发飞行事故。因此,还应当实时地就飞行速度进行保护,而这一点正是当前结冰边界保护研究中所缺乏的。
为实施对飞行速度的保护,首先须确立结冰后的失速速度值,这里采用一种简单估算方法,假设飞机在平飞状态下,重力等于升力,即
(40)
这样便可根据飞机在结冰情形下的最大升力系数CLmax_iced来估算出此时对应的平飞速度,即为最小平飞速度:
(41)
飞机油门的控制可采用简单的比例环节进行控制,结冰情形下的油门控制具体设计如下:
1) 当飞行速度大于或等于飞机的最小平飞速度,即V≥Vmin时,飞机的油门保持不变。
2) 当飞行速度小于飞机的最小平飞速度,即V δth=Kth(V-Vmin_iced) (42) 式中:Kth为常数。 需要指出的是采用式(41)计算出来的最小平飞速度偏于保守,这是因为忽略了推力克服重力的作用。考虑到飞机在实际的动态响应过程中,不可能一直保持平飞,但为了确保飞行安全,仍以最小平飞速度作为飞机飞行过程中的最低飞行速度限制。此外,考虑到外界扰动以及传感器误差等,将飞机的最低飞行速度限制为在最小平飞速度的基础上增加5%的裕度。 本文以构建的背景飞机为研究对象,飞机本体参数为:飞机质量m=42 000 kg,机翼面积S=124 m2,平均气动弦长c=4.15 m,展长b=34.10 m,Ix=1 151 900 kg·m2,Iy=2 392 630 kg·m2,Iz=3 846 326 kg·m2,Ixz=107 640 kg·m2。 飞机初始飞行状态设定为:飞行高度H=3 000 m, 飞行速度V=120 m/s,保持水平匀速直线飞行。当飞行指令设定为:βc=5°、αc=6°、μc=10°时,分别仿真出飞机在不含神经网络自适应环节与含有神经网络自适应环节的动态逆控制下,被控变量的动态响应变化。摄动参数的选取上,考虑内环控制回路中的A(x1)与外环控制回路中的G(xs1)无参数摄动、同时摄动-30%、同时摄动+30% 3种情形。仿真结果如图12和图13所示。 图12 含神经网络自适应环节的动态逆控制响应Fig.12 Response of dynamic inversion control with adaptive neural network 图13 传统动态逆控制的响应Fig.13 Response of traditional dynamic inversion control 采用传统非线性动态逆的控制参数设置为:ωα=2 rad/s,ωβ=2 rad/s,ωμ=2.5 rad/s,ωp=ωq=ωr=10 rad/s。 从图12和图13所示的动态响应曲线可以明显看出: 1) 在无参数摄动的情况下(蓝色曲线所示情形),不管动态逆系统中含不含神经网络自适应环节,飞机的被控参数β、α、μ均平滑地过渡到指令值,在过渡过程中没有超调量。 2) 对比迎角、侧滑角、航迹滚转角响应曲线可以看出,不含神经网络自适应环节的动态逆控制响应在参数摄动+30%及-30%的情况下很难使得系统达到预期的指令值,而且还可能会出现超调量。说明传统的不含神经网络自适应环节的动态逆控制对于模型参数摄动的鲁棒性极差。而含神经网络自适应环节的动态逆控制可有效减小系统的稳态误差,实现对飞机的被控参数β、α、μ指令值的精确跟踪,具有较强的鲁棒性,能显著改善系统在参数摄动情形下的超调特性。 从A(x1)与G(xs1)的组成元素可以看出,其中既包含气动参数,也包含飞机姿态角,也就意味着这两个矩阵的选取,既包含了结冰后气动参数获取不准确的可能,又包含了由于传感器误差带来的飞机姿态角测量有偏差的情形,因此是比较有代表性的。此外,还对A(x1)与G(xs1)均无参数摄动,A(x1)摄动+30%、G(xs1)摄动-30%,A(x1)摄动-30%、G(xs1)摄动+30% 3种情形的响应情况进行了分析,仿真结果同样证明了改进后的动态逆控制优异的控制性能,限于篇幅这里不再进行赘述。 综上所述,本文采用的基于神经网络自适应的动态逆控制器,不管是在控制的稳态响应及超调特性方面,还是在鲁棒性方面,都具有极大的优势。这两个方面的特性说明,只要动态逆控制器中的参数选取得当,飞机被控参数的动态响应就不会超出给定的指令值。 神经网络自适应动态逆控制具有良好的跟踪性能及稳态性能,可应用到飞行边界保护系统中对特定飞行参数进行保护。当飞机的被控参数选取为其边界值时,比如将结冰后的失速迎角值作为动态逆控制环节的输入指令,便可通过动态逆控制环节得到升降舵面的最大允许偏转角,飞机的边界保护系统实时地限制飞机的实际舵面偏角不超出该最大允许偏转角,这样飞机被控参数就始终能够在安全范围之内。这也就是本文提出的边界保护的核心思想。 仿真条件设定为:飞机在H=2 000 m高度上,以V=90 m/s的速度保持平飞,飞机在t=0 s时刻遭遇结冰,t=50 s时飞过结冰区,假设在此期间飞机结冰严重程度从未结冰线性增加至重度结冰,而后保持不变。根据结冰数据库得到该状态下飞机的失速迎角相应地从13°线性减小至7.5°。 飞机在t=0 s时刻收到驾驶员发出的θref=10° 飞行指令。分别在不开边界保护、只开迎角边界保护、迎角与飞行速度均边界保护3种情况下进行仿真,得到飞机各参数动态响应如图14所示。 从图14所示的仿真结果来看,随着结冰严重程度的增加,飞机的失速迎角逐渐减小、最小平飞速度逐渐增大。当结冰边界保护系统未开启时,飞机的迎角和飞行速度很快便超出了各自的边界值,极有可能引发严重的飞行事故。在只对单参数迎角进行边界保护时,可以看到虽然迎角被限制在安全范围内,但飞行速度逐渐低于最小平飞速度,同时不能够保证自动驾驶仪俯仰姿态保持模式的正常运行。在同时对迎角、飞行速度进行边界保护时,飞机的迎角与飞行速度实时地控制在不断变化的边界值范围之内,迎角距离边界的安全裕度相较于仅进行迎角保护时增大,同时保证了俯仰姿态保持模式的正常运行。以上的仿真结果可为结冰条件下驾驶员的合理操纵提供参考。在遭遇机翼结冰时,由于失速迎角的降低和失速速度的增大,首先宜增大油门,提高飞行速度,然后适当向前压杆,降低飞行迎角,并在整个调整过程中注意高度的变化。 本文提出的方法实现了对结冰飞行情形下两个关键安全参数(迎角和飞行速度)的边界保护。文献[3]中设计了PAH模式下的结冰边界保护系统,需要根据当前失速迎角、结冰严重程度与飞机飞行状态参数计算得到飞机的最大允许指令俯仰角,然后直接限制驾驶员给出的指令俯仰角值来保证迎角不超限。这就需要通过开展大量的仿真分析建立起最大允许指令俯仰角与失速迎角、结冰严重程度和飞行状态参数之间关系的数据库。相较于文献[3]中的方法,本文所提出的边界保护方法不用根据仿真计算得到当前状态下的最大允许指令俯仰角(如图7所示)来限制驾驶员俯仰角指令,而是直接根据失速迎角计算可用的舵面偏转角从而实现迎角的边界保护功能(如图11所示),实时性较好。 图14 结冰边界保护系统仿真结果Fig.14 Simulation results of icing envelope protection system 现有的结冰边界保护系统要么涉及到对飞机运动方程的积分来预测关键参数超限的时机及获取操纵舵面的最大允许偏转角,要么需要针对各种结冰情形与飞行状态开展离线数据库分析,耗费大量的前期计算工作时间与宝贵的机载计算机资源。本文提出了基于神经网络自适应动态逆的结冰情形下边界保护的方法,通过在动态逆环节中引入单隐层神经网络提升了动态逆环节的鲁棒性,消除了逆误差对整个系统的不利影响。此外,以结冰飞机最小平飞速度的估算值作为飞机最低飞行速度限制的原则,设计了自动油门控制系统,以实现对飞行速度的保护。通过仿真分析可以看出,采用神经网络自适应动态逆设计的控制律具有较强的鲁棒性。所提出的结冰边界保护系统,完全能够实现飞机在容冰飞行情形下的飞行安全。相比于传统的结冰边界保护方法,文中所提出的方法具有计算量小、鲁棒性强、实时性好,对飞行参数的保护更全面的优点,具有较高的工程应用价值。 由于本文采用神经网络进行在线补偿逆误差,补偿的效果由网络结构决定,即神经元的数目和类型及权重,调参难度相对较大,在逆误差很大时对在线神经网络的收敛性及算法的快速性要求较高。同时,本文以俯仰姿态保持为例进行结冰边界保护设计,主要针对纵向的关键安全参数进行边界保护。在下一步工作中,还将基于本文提出的方法针对横航向的关键安全参数(如滚转角、侧滑角、侧向过载等)进行边界保护和多参数飞行安全边界的确定方法研究。4 仿真验证
4.1 神经网络自适应动态逆控制鲁棒性验证
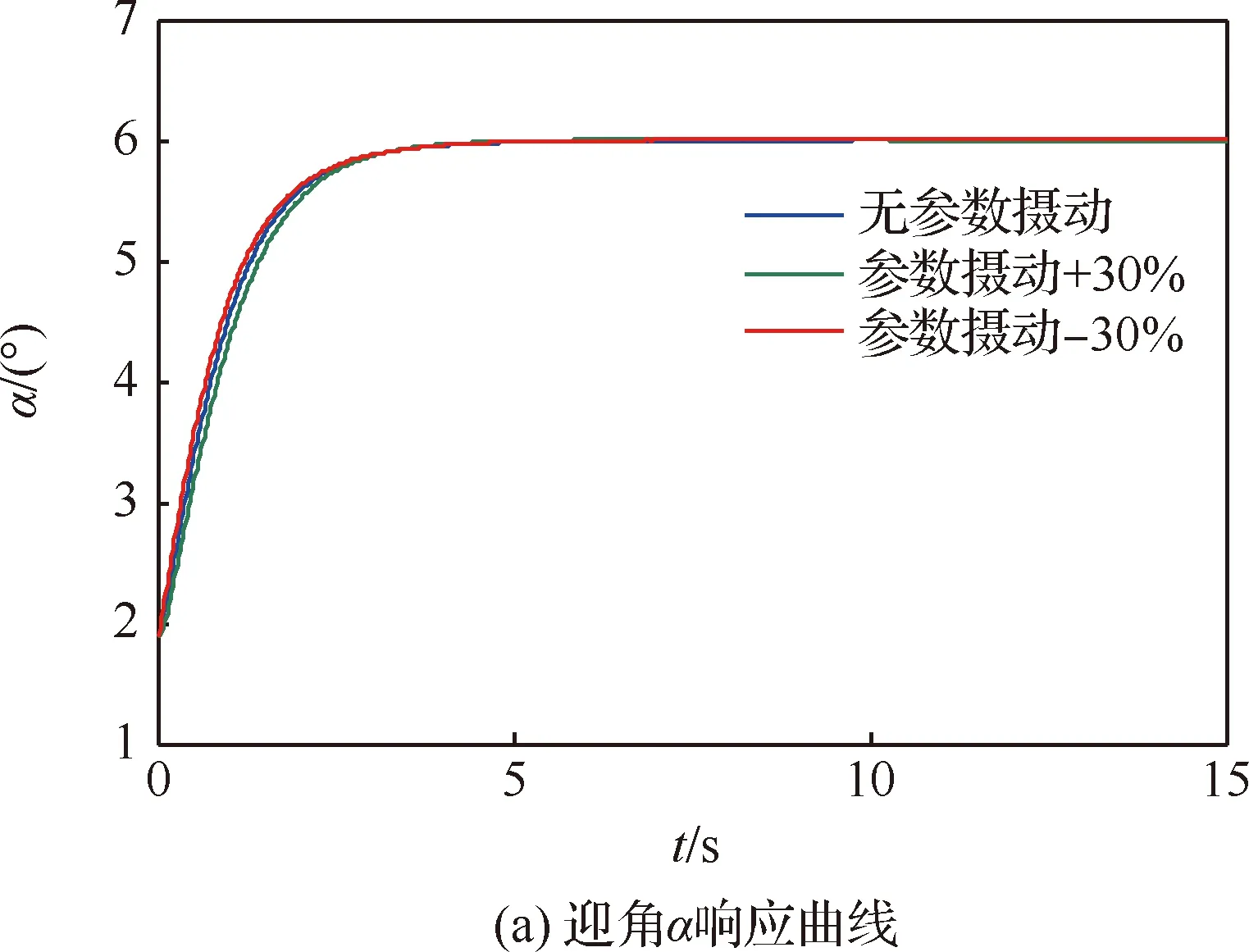
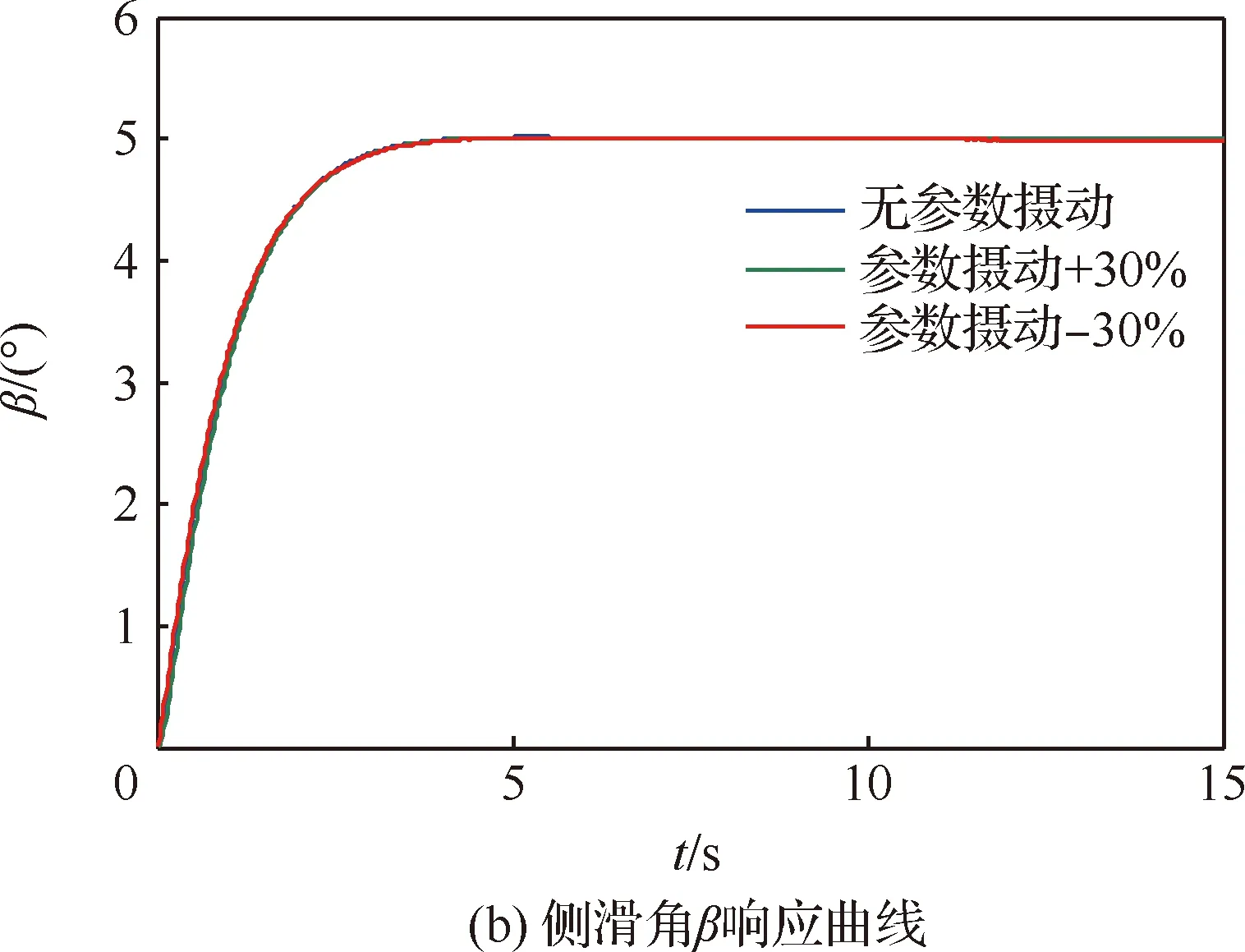
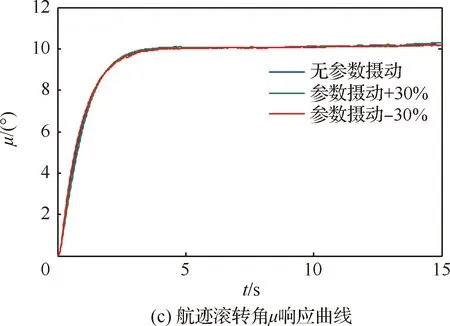



4.2 结冰边界保护系统仿真分析



5 结 论

