GEO星弹双基SAR多普勒分辨率特性分析

林春辉，郭苹，张林让，唐世阳,*，陈展野

1. 西安电子科技大学 雷达信号处理国家重点实验室，西安 710071 2. 西安科技大学 通信与信息工程学院，西安 710054

合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天候、全天时等成像能力，具有广泛的应用前景[1-5]。而作为一种新的成像体制，双基合成孔径雷达(Bistatic Synthetic Aperture Radar, BiSAR)与传统单基合成孔径雷达的区别在于发射机及接收机置于不同的平台上。收发分置的特殊几何结构使BiSAR相对于单基SAR具有隐蔽性好、安全性高；平台多样化、配置灵活；及获取更丰富的目标信号等优点[6-10]。

按收发平台的选择，现有的BiSAR主要体制可以分为机载BiSAR、星载BiSAR及混合平台BiSAR。其中，混合平台双基指的是发射平台与接收平台非同一类型的载体，如星机BiSAR、星地BiSAR、机弹BiSAR等。地球同步轨道(Geosynchronous Earth Orbit, GEO)星弹BiSAR是近年来出现的一种新型双基对地观察传感器。其中，GEO卫星的优势在于地面覆盖面积大，可实现全球成像；重访率高，有利于对目标地区的动态观察；同时由于轨道高度高，作为发射平台即使在空间导弹、激光武器飞速发展的今天也具有很高的生存能力[11-12]。但其空间分辨率低，而且收发平台都为GEO卫星需要较长的合成孔径时间才达到功率要求，这导致构建SAR几何构型时需要考虑地球自转等因素的影响。而传统的弹载SAR则可以实现距离方位的二维高分辨成像，但作为打击武器，其无法对前视目标区域成像，且作为主动侦察的辐射源与打击武器的结合体，其生存能力不够高。因此，GEO星弹BiSAR系统可以将星载SAR覆盖面大、安全性高与弹载SAR的高分辨、高机动性结合到一起，具有很好的应用前景。

分辨率分析是BiSAR系统的重要理论基础，决定了最后成像质量的高低，是获取高分辨图像结果的关键[13]。传统的SAR分辨特性分析主要集中在系统的带宽、合成孔径时间与二维分辨率之间的简单固定比例关系。对于单基SAR而言，其方位分辨率可以直观地定义为平台飞行方向最小可分辨单元，多普勒分辨率通常指垂直于斜距向的最小可分辨单元。传统收发天线速度方向相同的BiSAR同样可以有类似的推导。但GEO星弹BiSAR平台的几何构型相当复杂，首先GEO卫星的高轨道特点，导致必须考虑地球曲率、自转等因素，而导弹自身的运动也具有高机动的特点，同时两者时间的平台高度、飞行速度都有较大差异，无法严格定义方位向分辨率，系统的带宽、合成孔径时间与两维分辨率之间不再是传统的简单比例关系。

对于BiSAR分辨率分析，汤子跃和张守融从雷达方程的角度出发，给出了BiSAR距离分辨率和方位分辨率的特性研究[14]。其主要利用收发之间的几何关系，分析正侧视及斜视模式下的距离方位分辨率表达式。但该方法并没考虑收发平台之间不同的速度矢量，特别是速度方向对多普勒分辨率的影响。文献[15]结合梯度对星机BiSAR的距离及多普勒分辨率进行了数学推导，但其所分析系统的收发平台均处于匀速直线运动状态，没有考虑平台加速度对多普勒分辨率的影响。文献[16]提出了一种基于模糊函数分析的GEO BiSAR的分辨率计算方法，针对曲线轨迹的情况作出了一定程度的分析，但并不适用于GEO星弹BiSAR的多普勒分辨率分析。总体上，现有文献针对GEO星弹BiSAR系统，特别在合成孔径时间内，接收平台的运动轨迹为曲线轨迹的系统分辨率分析还不够完善，不利于后续成像算法的设计[17-18]。需要指出的是，这里的多普勒分辨率指的是多普勒梯度方向的空间分辨率大小，与传统的方位分辨率有一定的区别。本文针对GEO星弹BiSAR系统特殊的几何构型，简化发射平台的影响，重点分析接收平台的曲线轨迹对GEO星弹BiSAR系统的多普勒分辨率的影响，给出了相应的分辨率计算公式，最后通过仿真实验进行验证。

1 多普勒分辨率分析

在传统GEO-SAR单基系统或者GEO-LEO星载BiSAR系统的成像分析时，通常其合成孔径时间都相对较长，在百秒甚至千秒的量级。这是由于高轨的特点导致平均功率的下降，必须通过长时间积累获取足够的成像信噪比。而在GEO星弹BiSAR系统中，实际电磁波传播距离极大减小。因此无需过长的合成孔径时间，特别对于弹载平台而言，过长的合成孔径时间显然是不合理的。因此有必要重新对GEO星弹BiSAR系统的收发平台，特别是GEO卫星在较短合成孔径时间内的运动特点进行重新分析。

1.1 GEO卫星的运动分析

在传统SAR系统中，通常假设目标为静止状态，只有平台处于运动状态。而在GEO星弹BiSAR系统中，考虑地球自转的影响，目标随时间是转动的。为此，首先需要将卫星位置矢量转换到地固坐标系中。假设GEO卫星在轨道坐标系中的位置为Rg=[Xg,Yg,Zg]T，GEO卫星的轨道倾斜角为i0，升交点赤经为Ω0，近地点幅角为ω0，地球的自转角速度为ωe，方位时间为η，则GEO卫星在地固坐标系的位置矢量Rs=[Xs,Ys,Zs]T,且

Rs=M4M1M2M3Rg

(1)

式中:

(2)

(3)

(4)

(5)

传统对GEO卫星的轨迹分析通常都建立在长时间的基础上，所分析轨迹的持续时间通常在数千秒甚至几个小时的量级。在该情况下，GEO卫星的轨迹具有曲线轨迹特点，甚至在经纬度坐标中呈现“8”字型的轨迹形状[7]。但在GEO星弹BiSAR系统中，合成孔径时间并无需如此之长，此时GEO卫星的运动轨迹是否还存在曲线特性需要重新分析。根据式(1)，在合成孔径时间内，GEO卫星位置矢量在地惯坐标系中的变化情况如图1所示。从图中可以看出，在合成孔径时间内，GEO卫星的运动轨迹并非直线，因此其运动模型必须考虑加速度的影响。在地固坐标系中，目标为静止状态，卫星平台为曲线运动状态。

图1 GEO卫星轨迹图Fig.1 Trajectory of GEO satellite

1.2 GEO星弹BiSAR的模型分析

GEO星弹BiSAR的几何构型如图2所示。图中:Q、P分别为中心时刻收发平台的位置，l为平台运行轨迹；V为平台运动速度；A为平台运动加速度；R为瞬时距离，下标r表示接收机，下标t表示发射机；Rra为接收机到目标a的斜距矢量；Rrc为接收机到目标C的斜距矢量；Rta为发射机到目标a的斜距矢量；Rtc为发射机到目标C的斜距矢量；s为目标C到目标a的矢量。

根据几何模型，GEO星弹BiSAR系统的瞬时斜距历程可表示为

r(η;a)=|Rta(η;Rta 0)|+|Rra(η;Rra 0)|=

(6)

式中：η为慢时间；Rta 0为合成孔径中心时刻(Aperture Center Moment, ACM)发射机到目标a的瞬时斜距矢量;Rtc 0为ACM发射机到目标C的瞬时斜距矢量;Rra 0为ACM接收机到目标a的瞬时斜距矢量;Rrc 0为ACM接收机到目标C的瞬时斜距矢量。

图2 GEO星弹BiSAR模型Fig.2 Model of GEO missile BiSAR

1.3 GEO星弹BiSAR的多普勒分辨率分析

在传统BiSAR分辨率分析中，在η时刻，场景中目标a的多普勒频率表示为

(7)

式中：Uta和Ura分别为Rta和Rra的单位矢量；Vta和Vra分别为发射机及接收机相对目标a点的速度。对目标a的多普勒频率f(η;a)求梯度[14]：

(8)

则场景中目标a的多普勒分辨率大小为[15]

(9)

式中：Tsyn为合成孔径时长；ηc为合成孔径中心时刻。

从上述推导过可以看出，传统的多普勒分辨率分析并没有考虑加速度所带来的影响。且式(9) 中的计算方法仅适用于匀速直线的运动轨迹SAR。对于曲线轨迹SAR，如本文所提的GEO星弹BiSAR系统，会有较大误差。下面对GEO星弹BiSAR系统的多普勒分辨率进行推导。同样对场景中目标a点的多普勒频率进行推导，增加加速度的考虑，可得

fnew(η;a)=

(10)

对新的多普勒频率求梯度，可得

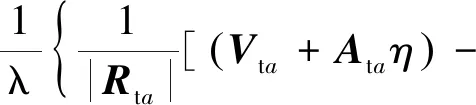
Uta

(11)

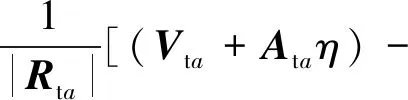
(12)

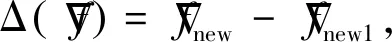
多普勒分辨率的大小指的是多普勒梯度方向上的分辨率大小，其大小与该点处的多普勒带宽大小相关，而多普勒带宽可以借助多普勒频率的梯度来获取[14]。在传统的SAR系统多普勒分辨率计算中，通常借助式(9)进行计算。但从式(12)可以看出GEO星弹BiSAR系统的多普勒频率梯度与方位时间相关，即具有方位空变性，传统多普勒分辨率计算方法失效。从物理本质上分析，在一定斜视角及波长条件下，BiSAR的多普勒分辨率大小取决于目标在合成孔径时间内对应收发天线的相干积累角之和，因此可以通过求解合成孔径时间内收发平台的天线相干积累角来求解多普勒分辨率的表达式。而相干积累角可以通过计算合成孔径时间内角速度变量的积分获得。而角速度变量为速度矢量与斜距矢量的比值，即

图3 忽略项带来的梯度误差Fig.3 Gradient errors caused by neglected terms

(13)

式中：V⊥为垂直于斜距矢量R的速度矢量。在本文应用场景中，发射平台所带来的影响可以忽略不计。结合式(12)，在合成孔径时间内，接收平台的角速度变量可以表示为[19]

(14)

多普勒分辨率可以表示为

(15)

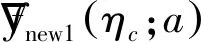
综合上述内容，虽然无法定义方位向，但可以结合梯度法及图像分辨率，对多普勒梯度方向及距离分辨率方向做简单的解释，如图4所示。Ur为距离分辨率的单位矢量。一般情况下多普勒梯度方向与距离分辨率方向并不相互垂直。图像分辨单元的面积可以表示为

图4 BiSAR的分辨单元Fig.4 Image pixel of BiSAR

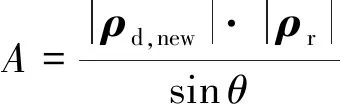
(16)

式中：|ρr|为距离向分辨率；θ为Ur和Ud的夹角。

2 仿真实验

为了验证本文多普勒分辨率计算方法的有效性，本部分将利用后向投影算法(Back Projection Algorithm, BPA)[21-24]所得的成像结果对多普勒分辨率进行估计，同时作为多普勒分辨率的理论对照值。仿真参数如表1和表2所示。

这里取场景中心点及边缘点的多普勒分辨率的数值进行对比说明。利用BPA得到两个点目标PT1(0,0) m，PT2(-400,400) m的多普勒梯度方向剖面图分别如图5(a)和图5(b)所示。定义-3 dB波束宽度为分辨率的大小，可计算得到PT1及PT2两点的多普勒分辨率分别为0.211 m 和0.212 m。

图6给出了利用本文式(12)计算得到的GEO星弹双基SAR多普勒分辨率等高线示意图。从图中可以看出，所提方法对PT1及PT2的多普勒分辨率计算结果分别为0.211 m和0.213 3 m。该计算结果与BPA聚焦算法所得到的理论分辨率值相比，误差远小于1%。

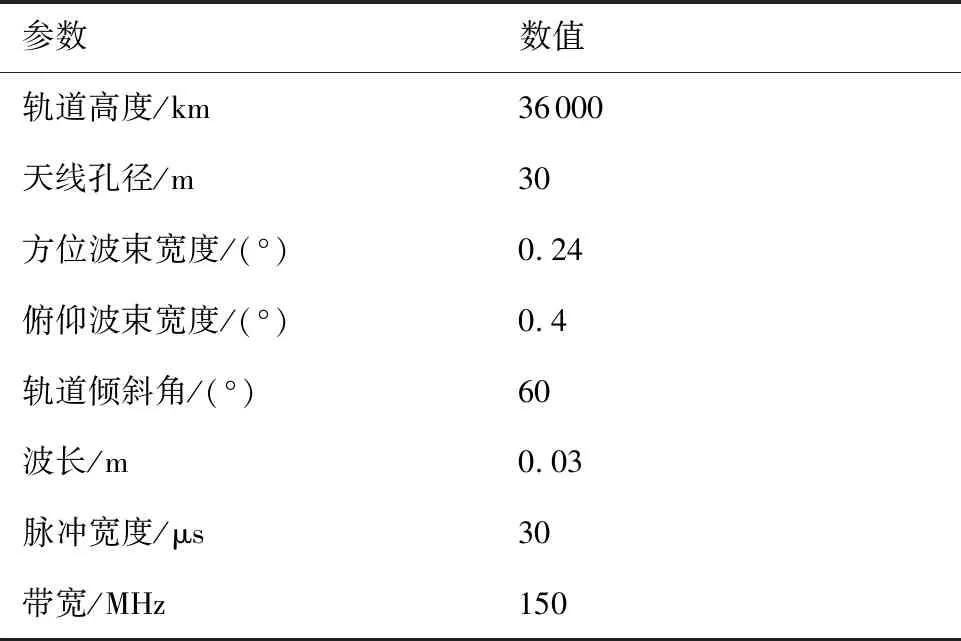
表1 GEO卫星参数Table 1 Parameters of GEO satellite

表2 导弹参数Table 2 Parameters of missile

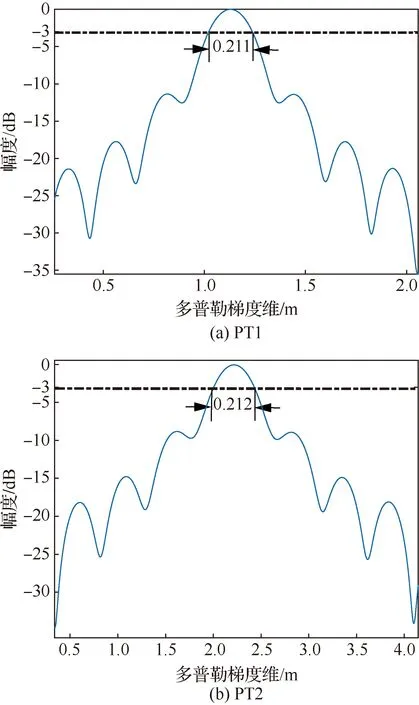
图5 利用BPA得到的点目标多普勒梯度方向剖面图Fig.5 Profile of point target obtained by BPA along Doppler gradient direction

图6 多普勒分辨率等高线图Fig.6 Doppler resolution contour map

为了进一步验证本文所提方法的准确性，本部分还将讨论传统方法[15]与本文方法所得的目标多普勒分辨率与理论值的误差随积分时间变化及接收端的入射角变化而变化情况，以场景中点目标PT2处分辨率为例。图7给出了相应的仿真结果，其中θRx为发射波束的入射角，图7(a)为传统方法多普勒分辨率计算误差的仿真结果，图7(b) 为本文所提方法多普勒分辨率计算误差的仿真结果。

从图7的仿真结果可以看出，当成像所需积分时间较小时，传统方法计算结果误差较小。但随着成像场景的增大或者分辨率要求变高，所需的积分时间变长，传统方法计算结果的误差急剧上升。本文所提方法计算结果的误差虽然随着接收端入射角变化会产生一定的变化，但误差远小于1%。上述仿真结果皆验证了本文所提多普勒分辨率计算方法的高精确度及有效性。

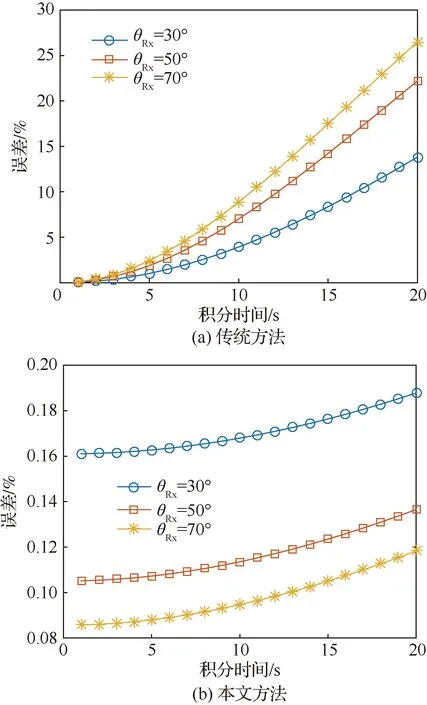
图7 多普勒分辨率计算误差Fig.7 Calculation errors of Doppler resolution

3 结 论

1) 对于GEO星机BiSAR系统，由于卫星曲线轨迹、地球自转、接收平台的机动性等因素影响，传统基于雷达平台匀速直线运动的多普勒分辨率计算方法不再适用。

2) 本文提出一种基于矢量分析的GEO星弹BiSAR多普勒分辨率计算方法。结合矢量分析可知，多普勒分辨率与收发平台的波束入射角、多普勒参数的大小及角度、积分时间有关。

本文所得到的多普勒分辨率计算公式考虑上述变化因素,仿真实验验证了所提方法的有效性。