超高速相干光通信两步步长优化CMA算法

钟 昆,杨怀栋

(清华大学 精密仪器系 精密测试技术与仪器国家重点实验室，北京 100084)

引言

相干光纤通信重新成为研究热点得益于高性能的激光器、低成本高速的ADC转换芯片，以及快速发展的数字信号处理(DSP)技术[1-7]。100 G及以上超高速相干光纤通信系统的发射机主要包括采用相位调制方式(例如QPSK)和偏振态复用的正交编码来传输[8-10]。接收机则采用相干检测技术，可实现光信号的相位信息、偏振态信息提取，从而使得高阶调制码型以及偏振态复用技术的实现成为可能，并可大幅提升系统的频谱利用率[11-13]。相干检测技术还可大幅减少接收机噪声灵敏度限制。

随着DSP技术的快速发展，通过DSP来补偿传输损伤的高速相干光通信系统被相继报道[14-18]。QPSK调制格式由于具有较高的频谱利用率、较强的抗干扰性和电路上易于实现，在实际光通信包括自由光通信系统[19]中得到了广泛的应用。又由于QPSK信号具有恒模特性，加上偏振模色散PMD引起的传输信道不断变化，所以通常采用具有恒模盲均衡性质的CMA算法进行PMD色散补偿和偏振解复用。CMA算法利用传输光信号的包络是常数的特点，不需要其它任何先验训练序列，具有计算复杂度低、易于实现等优点，体现了很强的应用前景。在传统的CMA算法中，其步长系数的取值严重影响着算法收敛速度、误差矢量幅度(error vector magnitude, EVM)和误码率(bit error ratio, BER)等性能评价。提出并验证了一种优化的CMA算法，其具有两步步长系数，可标记误差矢量函数曲线稳定时的区间，能够改善解调性能，降低系统的EVM。

1 原理

CMA算法的代价函数[20]通常写为

J(w(n))=E[(|y(n)|2-Rp)2]

(1)

w(n+1)=w(n)-μx(n)e*(n)

(2)

式中：μ为CMA步长系数；e(n)为估计误差矢量信号，其表达式为

e(n)=y(n)[|y(n)|2-1]

(3)

在偏振复用系统中，X偏振分量和Y偏振分量需通过蝶形滤波器实现CMA算法的输入输出和权向量更新。

1.1 标准CMA算法

首先设定抽头权向量初始值[21-22]，即将4个迭代系数初始化为w11=[0,…,1,…,0]T，w12=[0,…,0,…,0]T，w21=[0,…,0,…,0]T，w22=[0,…,1,…,0]T。

将输入信号Xi/Yi截取为长度等同于滤波器抽头数量L，步进为M的子输入信号xk/yk。

根据蝶形滤波器原理，CMA算法处理后的输出信号Xo/Yo与处理前的输入信号xk/yk之间的关系是：

X0=xk·w11+yk·w12

(4)

Y0=xk·w21+yk·w22

(5)

(3)式与X/Y偏振态对应的误差函数ex/ey可写为

ex=(R1-|Xo|1)Xo

(6)

ey=(R2-|Yo|2)Yo

(7)

式中R1=R2=1。

4个迭代系数w11、w12、w21和w22按(8) 式进行更新：

w11=w11+μ·xk′·ex

(8a)

w12=w12+μ·yk′·ex

(8b)

w21=w21+μ·xk′·ey

(8c)

w22=w22+μ·yk′·ey

(8d)

上述即常规CMA算法的具体实施方式。

1.2 两步步长优化算法

本文提出的两步步长优化算法的原理描述如下。

1) 采用逐试法为变换μ值，以不断地重复常规CMA算法，例如设置变换μ值的区间为[0.001,0.08]，步进为0.001。每一个μ值实施的CMA算法，记录对应输出信号的EVM和BER。

2) 以最小的EVM/BER对应的步长值作为最优步长系数，设为μ0。画出此时的误差矢量函数曲线ex0(k)。

3) 与步长系数和误差矢量函数相关不同[20]，这里只确定一个步长系数μ1(其值为μ0/3或μ0/2)，使得此步长系数具有较小的收敛稳态值。

4) 估计误差矢量函数曲线趋于稳定的区间方法：设置区间例如L=20，计算区间内误差矢量函数的均值和标准差，若相邻区间的均值和标准差变化率小于某值(例如15%)，表明此区间误差矢量函数趋于稳定。设置区间内的一个符号所在的位置标记为k0。

5) 进行两步步长优化设置方法：当符号所在的位数kk0时，步长值设为μ1。画出此时的误差矢量函数曲线ex1(k)。

6) 将误差矢量函数曲线ex1(k)，与固定步长的误差函数曲线ex0(k)进行比较，对此算法的优化改善程度(EVM, BER以及误差矢量值等)进行评价。

2 仿真与讨论

2.1 仿真结构原理

仿真采用的100 G PM-QPSK相干光通信系统的发射机、光纤通信信道和接收机如图1所示。在发射机部分，激光器输出载波波长为1 550 nm，激光的线宽和频偏在合理区间范围内任意可调。信号发射器发射25 GHz非归零码(not-return-to-zero, NRZ)伪随机微波信号作为马赫-曾德调制器(mach-zehnder modulator, MZM)的调制信号[7]。激光器发出的偏振光通过偏振分束器1(polarization beam splitter, PBS)和偏振控制器1(polarization controller, PC)分成两路载波信号，分别形成X和Y偏振支路的I/Q支路载波信号。而4路调制信号则通过2个MZM调制器调制后，已调制的光信号通过偏振合束器1(polarization beam combiner, PBC)形成100 GHz偏振复用光信号，并发射进入光纤通信信道进行信号传输。PC2和PC3分别调节使得上下两路的载波光偏振态正交。在光纤信道传输部分，由一段100 km的单模光纤和EDFA组成。在接收机部分，接收到的偏振复用信号首先通过调节PC4和PBS2，使得这两路偏振态正交的光信号与发射端的光偏振态有关。这个过程被称为“偏振解复用”。将此两路信号光分别与本地震荡器(local oscillator, LO)的两路偏振态正交光信号(通过调节PC5和PBS3)，一起送入90°混频器1和2进行相干解调，并通过平衡探测器(balanced detector, BD)1到4形成4路原始的模拟电信号。4路模拟电信号分别通过模数转换器(analog-digital-convertor, ADC)将4路模拟信号转换为数字信号，并最终送入计算机或现场可编程逻辑门阵列(field programmable gate array, FPGA)进行后期DSP处理。DSP处理模块依次通过重采样、色散补偿、偏振解复用补偿(CMA算法)、载波频差补偿和载波相位补偿。最终在计算机上进行接收机DSP补偿效果的EVM/BER的性能分析。

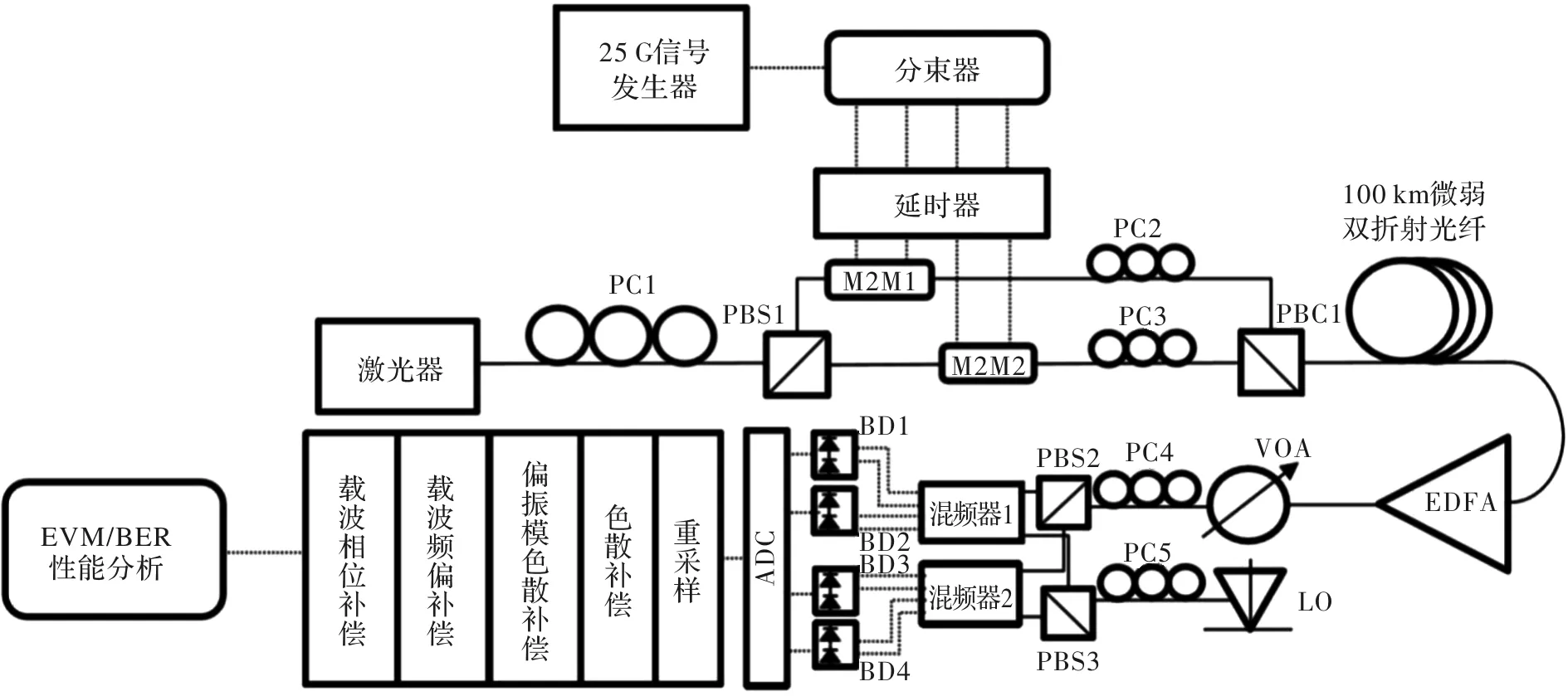
图1 100G PM-QPSK相干光通信系统的仿真平台Fig.1 Simulation platform of100G PM-QPSK coherent optical communication system

2.2 数值模型和计算过程

根据图1的100 G PM-QPSK相干光通信系统的仿真平台，首先以流程图的形式，画出其数值模型和计算过程如图2所示。其中Dp为偏振模色散系数，lc为光纤的相关长度，Δβ1为光纤的双折射。

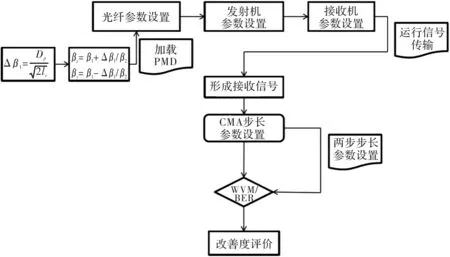
图2 100G PM-QPSK相干光通信仿真数值模型和计算过程Fig.2 Numerical model and simulation process of100GPM-QPSK optical communication simulationplatform

(1)

βx=β1+Δβ1/2

(2)

βy=β1-Δβ1/2

(3)

式中：β1、βx和βy分别为一阶传播常数，x和y为2个偏振方向的传播常数。

接下来进入到接收机的DSP处理。对于偏振解复用或偏振模色散补偿，首先采用标准CMA算法扫描步长系数μ区间[0.001,0.08]。此时计算每一个步长系数值CMA算法对应的输出信号的EVM和BER值。计算得到当μ值0.017时，此时的CMA输出信号拥有最小的X/Y偏振态EVM值，此时的EVM为37.99%/39.52%。同样，当μ值取0.018时，此时的CMA算法输出信号拥有最小的X/Y偏振态平均BER为2.61%。

接下来进行两步步长参数设置。首先画出标准CMA算法的误差矢量函数曲线ex0(k)。设置区间L=50，计算区间内误差矢量函数的均值和标准差。当k=351时，相邻区间的均值和变化率均小于15%，可认为此区间误差矢量函数趋于稳定。设μ1=0.01≈μ0/2。实施优化的CMA算法：当k<351时，步长系数μ取0.018；当k≥351时，步长系数取0.01。

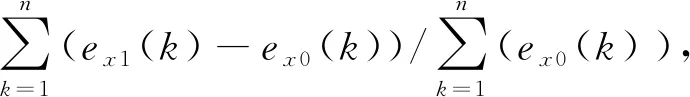
图3 标准CMA算法(实线)和两步步长优化CMA算法(虚线)的误差矢量函数Fig.3 Error vector function of standard CMA (solid line)and proposed two-stage optimized CMA(dotted line)

最后计算PMD取值范围[0.131,0.140]，考察EVM和BER的改善率。在表1中，单步标准CMA算法的X、Y偏振态EVM，X/Y偏振态平均BER为EVM_x0, EVM_y0, BER_x0+y0；两步步长CMA算法的X、Y偏振态EVM，X/Y偏振态平均BER为为EVM_x1, EVM_y1, BER2_x1+y1。这6列数据是分别计算标准和两步步长优化算法的EVM/BER获得的。

在表1中的ΔEVM_x(%),ΔEVM_y(%)以及ΔBER_x+y(%)这3列的改善程度量化分别通过如下公式获得的：

(4)

(5)

由 (4)式和(5)式计算可得，在PMD区间为[0.130,0.140]时，优化的CMA算法对X偏振态的EVM平均改善率为4.73%，对Y偏振态的EVM平均改善率为5.33%；BER的平均改善率为4.27%。

表1 PMD色散系数与标准CMA和两步改进CMA算法的EVM/BER的值

3 结论

提出了一种改进型两步步长CMA算法。其相比标准CMA算法具有解调性能的提升，对EVM和BER有4%～5%的改善，对误差矢量函数也有约2%～3%的改善。提出了一种寻找误差矢量函数稳定区间的方法，是实施优化CMA算法不可或缺的一部分。后续的工作可寻求变步长的方式，从两步步长到多步步长变化，比如步长值与误差矢量函数值有关。

致谢

肖晓晟老师对本文具有重要的贡献，在此表示感谢！