基于大气湍流光闪烁的真随机数提取研究
亢立明,姚海峰,陈纯毅,刘中辉,向 磊
(1.长春理工大学 光电测控与光信息传输技术教育部重点实验室,吉林 长春 130022;2.长春理工大学 计算机科学技术学院,吉林 长春 130022)
引言
随机数提取是密码学及信息安全领域中一个重要的问题,如何得到随机性好的随机数在信息安全领域受到广泛的关注[1]。产生随机数的方式总的来说有两种:一种是通过伪随机数发生器(pseudo-random number generator, PRNG)产生,另一种是通过真随机数发生器(true random number generator, TRNG)产生。伪随机数是通过数学方法由计算机产生的,它与真随机数相比最大的区别在于能否对下次结果进行预测。伪随机数生成器虽然快捷,但是它产生的随机数是先定的,具有周期性。在加密应用中,如果攻击者拥有足够的计算能力,则可以对伪随机数加密进行破解。真随机数发生器通常利用一些不确定的熵源[2],从某种物理现象(如大气噪声,热噪声,电路噪声,放射性衰减等)提取随机数[3-6],利用这种方法生成的随机数通常可以认为随机性很高。Intel公司曾利用电阻热噪声设计出一种随机数发生器[7]。成都电子科技大学的张传武、彭启宗等人[9]在S.Wolfram提出的利用细胞自动机产生随机数方法[8]的基础上,进行了深入研究,提出了基于具有本原多项式的90/150加性细胞自动机的随机数发生器模型,得到了随机性更好的结果。
大气层中空气密度的无规则起伏称为大气湍流[10]。大气湍流运动引起大气温度和密度随机变化,从而导致大气折射率随机变化;折射率的随机起伏会使湍流中传输光波的光场参数产生随机起伏,进而引起光束抖动、强度起伏、光束扩展和像点抖动等一系列光传输的大气湍流效应[11]。正是由于湍流效应的随机性,可以认为大气湍流是一个随机的物理熵源,能被用作真随机数的提取。最近,Margano等人[12]尝试利用大气湍流产生的光起伏作为随机数发生器的物理熵源来提出真随机数,Gilbreath和Restaino等人[13]提出使用自校准Mach-Zehnder干涉仪来收集通过在大气中传播的光束的时域相位波动,将记录的相位波动转换成随机位流的方法。
本文提出根据在大气湍流中闪烁的光斑图像的特征,来实现真随机数的提取。光在大气湍流中传输受到湍流影响,导致接收的光斑图像发生变化,这种变化属于物理过程,具有不可预测性,可将其作为真随机数提取所需的熵源。在接收到闪烁光斑图像后,对图像进行处理,利用算法可从中提取随机数。
1 基于闪烁光斑图像的真随机数提取理论
如图1所示,在发射端发射波长为532 nm的激光,激光光束经过大气信道,受到大气湍流的影响最终到达接收端,接收端使用CMOS相机获取图像信息,并通过计算机中的相机软件采集到实验所需的光斑图像。

图1 大气信道模型与光斑图像采集装置Fig.1 Atmospheric channel model and light spot imageacquisition device
激光在大气湍流中传输一定距离后,其光密度在空间和时间上发生变化,这种变化是因为激光在传播时,沿途温度变化而引起的大气折射率变化。大气信道各部分就像棱柱和透镜,它使通过的激光束产生偏折,由于风可使湍流跨过光束横向漂移,所以偏斜方式随湍流气体通过光束的时间有关。如果在湍流大气中与光源相距一定距离处测量光的强度,会出现光强I随时间围绕平均值作随机起伏的现象。这一点可以用功率监测值说明,接收器接收的光强忽大忽小,变化频率快且波动范围大。可用归一化光强起伏方差来表示光强起伏强弱程度,它的定义[14]为
(1)
其中尖括号表示求系综平均。光强起伏方差较大的时候,表明光强起伏程度较大。实验中,观察光功率计,在数值变化起伏大的时候,通过改变相机采集图像的时间间隔来获取一定时间内连续变化较明显的光斑图像。
根据我们提取的受大气湍流影响的光斑图像[15]进行真随机数的提取。由于接收到受湍流效应影响的图像中像素点会产生无规则变化,这种变化属于物理过程,以此来作为真随机数提取的熵源。对这种随机变化的像素点作计算,即可以得到随机的结果。首先,在光斑图像上选定一个网格H,网格中包含一定的像素点,然后通过设定一个阈值v,选择网格中灰度值大于v的像素点作为选定的点,按照其所在位置进行排序,这样我们就得到了一个有序序列Sf,即
Sf={s1,s2,…,snf}
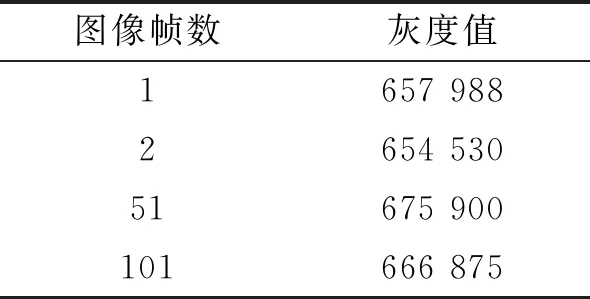
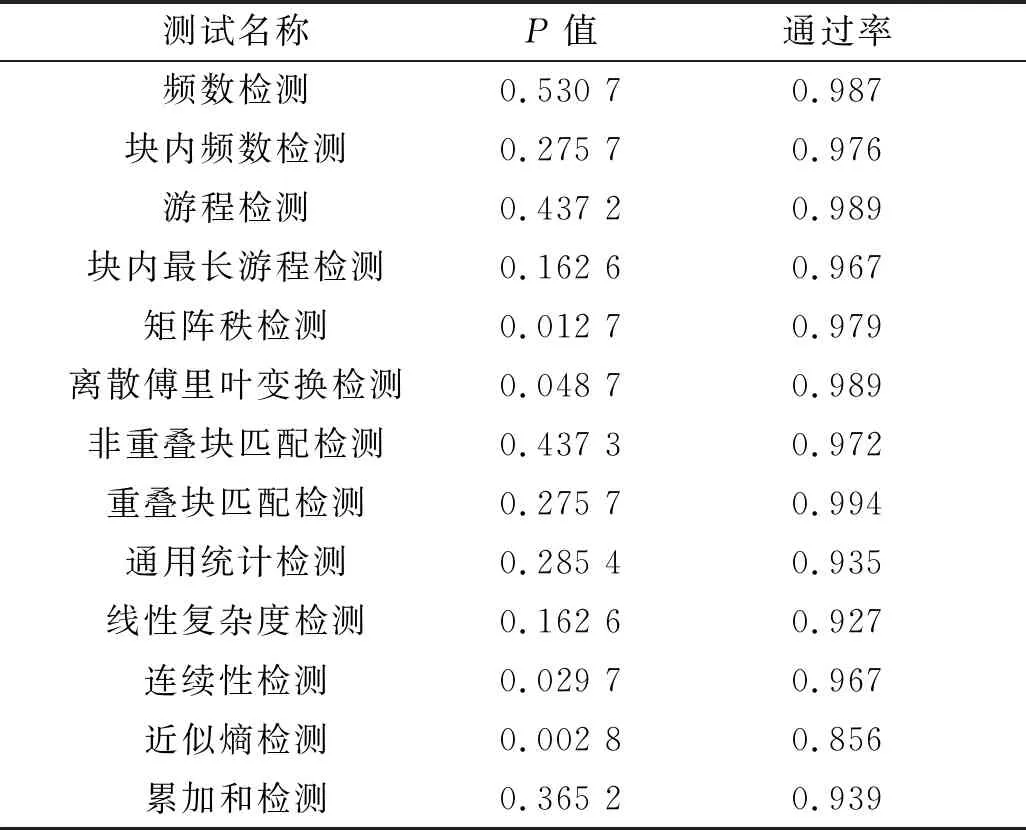
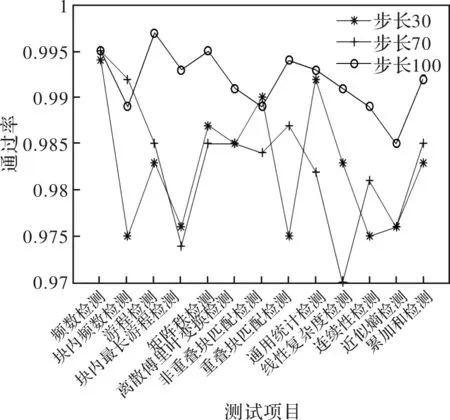
其中s1 (2) 式中:Tf为网格H中所有选定点可能的组合;N为网格的格子数量;nf为选定点的数量。对于每一组Sf,可以得到I(Sf)与之相对应[12]: (3) 式中:0≤I(Sf)≤(Tf-1);I(Sf)为每一组网格中选定点的组合;sk为网格中每一个选定点的位置。(3)式给出了在一个网格中对应于一组Sf所确定的组合数,而真随机数提取正是通过Sf与I(Sf)的一一对应关系来提炼随机性,这样,就得到了一个随机的整数。 为了将在区间[0,Tf-1]内的随机整数I(Sf)转换为无偏位流序列,可以考虑Tf的二进制拓展: Tf=2L+αL-1·2L-1+…+α0·20 (4) (5) 在公式(5)中找到最大的m,并提取I(Sf)的二进制扩展的前m位,通过这个规则可知,当I(Sf)<2L时,所取的对应位数为L,当2L 图2 基于大气湍流传输光斑图像的随机数生成原理图Fig.2 Schematic diagram of random number generationbased on transmission light spot image inatmospheric turbulence 与传统的真随机数提取方法相比,本文提出了根据在大气湍流中闪烁的光斑图像的特征进行随机数的提取。本文的方法在光斑图像的获取上作出改进,通过对采集的图像信息进行两种不同的选取方式,分别为固定间隔选取和多步长间隔选取,得到相关性较弱的光斑图像。通过在图像上选取随机网格,在网格中设定阈值,选取随机像素点的方式,计算每一个网格中的组合数I(Sf),实现随机数的提取。算法的基本流程如下: 1) 从计算机端接收到若干光斑图像,即{f1,f2,…,fn}。 2) 通过两种方法分别对光斑图像进行选取。第一种为固定间隔选取,即在每间隔固定的帧数R时,选取一张图像。第二种为多步长间隔选取,即设定几个步长x,在x范围内随机选取一张图像。 3) 光斑图像选取之后,找到图像上光斑变化的部分,随机选取一个网格H。 4) 网格选取之后,设定一个阈值v,在网格H中确定选取的像素点。 5) 最后计算出I(Sf)的值,进行随机数提取。 在光斑图像的选取中,通过固定间隔选取和多步长选取两种方式来选取光斑图像。由于光斑图像上存在灰度值为零的位置,而灰度值为零表明该位置没有光斑。因此,需要选择有光斑图像存在的位置进行随机数提取,如图3所示。 图3 简化光斑图像前后对比图Fig.3 Contrast diagram of simplified light spot image 固定间隔选取是通过在连续的光斑图像中,找到一个固定的间隔R,每间隔R值后,选取一张光斑图像。为了确定R值,可以计算出光斑图像上选择区域的灰度值之和,并画出灰度值随帧数变化的曲线,如图4所示。从图4中可看到,曲线起伏变化明显,选择两张灰度值相差较大的光斑图像,这两张图像的间隔数作为固定选取的间隔。 图4 灰度值随帧数变化的曲线(某个样本)Fig.4 Gray value versus number of frames (a sample) 多步长选取是通过在选定的步长内随机选取某一帧图像f来实现光斑图像选取的随机性。实验过程中,设定了3个不同的步长,分别为x1,x2,x3,在每一个步长内随机选取一个k值,nx 为了确定选取的光斑图像是否符合随机性要求,可以根据选取的相邻光斑图像fn和fn-1的相关性来确定。对于固定间隔选取方法,计算出第一张图像与第二张图像的相关系数ρ1,第一张图像和与它相隔R帧的光斑图像之间的相关系数为ρ2,通过对比相关系数ρ2与ρ1,可以确定固定间隔选取的图像相关性的强弱;对于多步长选取的情况,可以在选取的多张光斑图像中,选择2张相邻的光斑图像并计算他们的相关性,即第n张与第n+1张光斑图像的相关系数ρn,其中n=1,2,3…。根据(6)式进行相关性计算: (6) 式中:Cov(X,Y)为X、Y的协方差;D(X),D(Y)分别为X、Y的方差。通过计算得到的相关系数,可以判断选取的光斑图像之间的相关性,当相关系数在0.3以下时为弱相关,能够用于随机数的提取。 在光斑图像上选取一个5×5的网格H,选取的具体过程是通过在光斑图像确定的区域上随机选取一个点A,再以A点为中心,在其左右、上下进行扩充,成为一个5×5的网格,即{a1,a2,…,a25},具体选取方法如图5所示。 图5 随机网格的选取方法图Fig.5 Selection method diagram of random grid 确定了光斑图像上的网格H之后,需要进行阈值v的选取,以确定选取的点。阈值v的选取可以分为很多种,这里我们选择网格内的像素最大值与最小值的均值作为阈值。在网格序列{a1,a2,…,a25}中找到灰度值最大的像素点amax,以及灰度值最小的像素点amin,即阈值v为 (7) 将网格内大于v的像素点作为选取的点,可以得到一个有序序列Sf={s1,s2,…,snf},通过(3)式计算出与其相对应的I(Sf)的值。得到I(Sf)的值之后,将I(Sf)的值展成二进制的形式,即: I(Sf)=2L+βL-1·2L-1+…+β0·20 (8) 其中βk=0,1,这样就得到一个由0和1组成的位流序列,先通过(5)式计算得到m值,即选定位数,再通过选择I(Sf)二进制形式的前m位,便可以得到一个随机序列。通过对每一张选定的光斑图像进行随机序列提取处理,可以提取出多组随机序列,再将他们组合起来,实现随机数的提取。 本文采用532 nm波长激光进行传输实验,发射端位于长春理工大学科技大厦13层,接收端位于长春理工大学第二教学楼9层,发射端与接收端相距860 m。在发射端,激光通过光束准直扩束系统的扩束后,压缩束散角进入大气信道,光束准直扩束系统下端安置了三维电动调整台,实现对发射端高度,俯仰角和转角的高精度调整,如图6(a)所示。在接收端,采用透射式望远系统对入射光进行接收,然后使用CMOS相机获取光束信息,再通过在计算机中的相机软件查看并获取光斑图像,如图6(b)所示。其中相机型号为CAMM1362高速可见光相机,其曝光时间为0.02 s,像元尺寸为480×480,像元数为230 400像素。 图6 激光传输实验装置Fig.6 Laser transmission experimental device 实验过程中,通过上述实验装置获取了10 000帧光斑图像。前面提到激光传输受湍流效应的影响,光强产生随机变化,通过光功率计来实时监测,在相机曝光时间的选择上,我们通过观察光功率计上的数值,在数值变化较大的时候,通过调整相机采集图像的时间间隔来获取一定时间内连续变化较明显的光斑图像。另外,在像元尺寸的选择上要保证能够采集到完整的光斑图像。此次实验相机采集的时间间隔为0.02 s,在每隔1 s时选取一张光斑图像,即R=50帧为一个间隔进行光斑图像的选取。图7给出了间隔后的图像与连续图像的对比。从图7可以看出,第1张光斑图像与第2张光斑图像差异很小,这说明获取前两张图像的时间间隔很短,激光传输受到湍流效应的影响基本相同,而在间隔了50帧之后,第51张图像与第1张有明显差异,第101张同样也与其有明显差异,表明激光传输受到湍流效应的影响不同。表1给出了这4张图像的灰度值大小。从表1可以看出,与连续图像相比,间隔50帧后的图像灰度值差距较大。 表1 光斑图像的灰度值 为了进一步验证能否用于随机数的提取,可以判断选取的光斑图像的相关性。通过(6)式计算光斑图像间的相关系数,可以计算出第1张图像与第2张图像的相关系数ρ1=0.996 7,第1张图像与间隔50帧后的图像相关系数ρ2=0.269 8,再次间隔50帧后的图像相关系数为ρ3=0.184 6。从相关系数可以看出,连续的光斑图像之间的相关系数很大,接近于1,说明两张图像相关性很强,变化特征基本相同,不适合随机数的提取;而第1张光斑图像与间隔50帧后的图像间的相关系数小于0.3,属于弱相关,说明两张图像变化特征不同,可以进行随机数的提取。 图7 湍流效应下的光斑图像Fig.7 Light spot image in turbulence effect 为了检测提取的随机序列的随机性,我们采用美国国家标准与技术研究院NIST(National Institute of Standard and Technology)提供的STS随机序列检测包[16]。NIST测试主要用于检测随机数产生器所产生的随机序列的随机性,各项测试及物理意义[16]如表2所示。每项测试会输出一个P值[16],当所有测试项的P值大于最小基准线α=0.01时,可以认为测试的随机序列有较好的随机性。对固定间隔选取的实验中得到的随机序列进行测试,得到的结果如表3所示。 从表3的测试结果中可以看到,固定间隔选取的方法提取的随机数没有达到很好的随机效果,测试项‘近似熵检测’的P值低于0.01,表明没有通过测试。产生这种结果的原因可能是,大气湍流效应在某一短时间内,难免会出现变化很小的时候,而激光传输的速率很快,在固定间隔选取光斑图像时,可能会存在选取的相邻的图像恰好是相关性较强的图像,使得提取的随机序列存在相关性较强的部分。为了避免出现这种情况,可以采用多步长内随机选取的方法。 表3 固定间隔选取的NIST随机性测试结果 对于多步长选取的方法,为了与固定间隔选取方法进行对比,在步长的选取时,需结合灰度值与帧数曲线,在固定间隔R的附近进行选取,同时为了最大化的利用光斑图像,步长不宜选择过大。本文经过多次实验的模拟、测试,得出的结果中,在步长50附近选择了x1=30,x2=70,x3=100作为实验选取的步长。在步长范围内随机选取一帧图像作为选取的光斑图像。图8给出了步长为70时,选取的相邻的3张光斑图像,选取的3张图像间存在明显的差异,表明激光传输受到湍流效应的影响不同。同样通过(6)式计算相关系数并判断相关性,可得在步长x1=30时,选取的前两张光斑图像的相关系数ρ1=0.145 1;步长x2=70时,选取的前两张光斑图像的相关系数ρ1=0.024 2;步长x3=100时,选取的前2张光斑图像的相关系数ρ1=0.082 1。从相关系数可以看出,选取的光斑图像的相关性很弱,相比于固定间隔选取下的相关系数,多步长选取条件下的相关系数更小,说明选取的图像相关性更弱,提取的随机数的随机效果可能更好。在多步长选取的条件下,依旧采用NIST测试软件进行随机性测试,测试的结果如表4所示。 图8 多步长选取的相邻的光斑图像(步长70)Fig.8 Adjacent spot image selected by multiple steps(step70) 通过对比表4与表3的测试结果可以看出,在固定间隔选取光斑图像的时候,我们得到的测试结果一般,存在P值小于0.01的情况,并没有达到最好的随机效果;相比之下,在多步长选取光斑图像的条件下,得到的测试结果表明随机性的效果很好,其P值均大于0.01,通过率更高,可以判断得到的序列是随机的。 为了对比3种步长条件下最优的情况,我们可以通过作出P值曲线与通过率曲线,来直观的找到哪一种步长下的随机效果更好。P值曲线如图9所示,通过率曲线如图10所示。从图9中可以看出,在3种步长的结果中,P值的大小不一,其中在步长为100的时候,得到的P值在多数情况下相比于其他两种步长更大。同样从图10中可以看出,3种步长的通过率均在0.97以上,其中步长为100的时候,总体的通过率要高于其他两种步长。由此可以看出,在步长30、70和100的条件下,步长选取100的时候,能够得到随机性更好的结果。 表4 多步长选取的NIST随机性测试结果 图9 3种步长的P值曲线Fig.9 P-value curves of three steps 图10 3种步长的通过率曲线Fig.10 Passage rate curves of three steps 本文重点进行了在多步长间隔内随机选取光斑图像的方法,与文献[12]中连续帧光斑图像进行随机数提取相比,避免出现随机性相近的光斑图像,从而影响提取的随机数的随机效果;比较了固定间隔选取与多步长选取光斑图像,得到了更优的真随机数。在真随机数提取时,如果采用本文的方法进行随机数的提取,相比与文献[12]中提出的连续帧光斑图像的随机数提取方法,测试结果的P值更大,最高可以达到0.8以上,通过率能够达到0.985以上,说明提取的随机序列效果更好。 通过接收在大气湍流中传输的532 nm波长激光光束,采集了光束受湍流效应影响所产生的光斑图像,给出了在大气湍流中闪烁的光斑图像的特征,实现了真随机数提取的方法。采用固定间隔选取和多步长选取的方式,对光斑图像进行选取。之后在光斑图像上选取网格,通过选取网格中的像素最大值与最小值的均值作为阈值,来确定网格中选取的像素点,提取出了随机数。最后对两种方式提取的随机数分别进行随机性测试,实验结果表明,在固定间隔选取时,可能存在选取的相邻图像相关性很高的情况,得到的结果可能会不符合随机性要求;多步长选取的方式进行随机数的提取中,设定了30、70和100这3种步长,能够避免出现选取的光斑图像相关性高的问题。运用NIST随机性测试软件对所获得的随机序列进行测试,测试结果表明,多步长选取的方式相比于固定间隔选取的方式要有更好的随机性,测试结果的P值均大于0.01。从使用的3种步长结果来看,在步长为100的测试结果中,多数情况下P值要比其他两种步长大,通过率均在0.985以上,说明当步长选为100时,可以获得随机性更好的随机数。在实际应用中,用本文提出的随机数提取方法能够得到随机性较好的真随机数,可为信息安全领域中的真随机数提取提供借鉴。

2 真随机数提取的实现
2.1 光斑图像的选取


2.2 随机网格选取及阈值确定

2.3 随机数提取实现
3 实验与结果分析





4 结论

