基于光杠杆的弯曲法杨氏模量测量研究
刘道军,程 冬
安徽新华学院公共课教学部,安徽合肥,230088
1 相关研究与问题提出
物理学中固体在外力作用下发生形状的变化称为形变。在胡克(R.Hooke)定律范围内的形变都是可恢复的,称为弹性形变。一般地,在工程技术上,反映材料从不同角度抵抗形变能力的物理参数通常有杨氏模量、剪切模量和体变模量。其中杨氏模量是反映材料抗拉伸形变的物理量[1-4]。杨氏模量的测量方法主要分为两大类:拉伸法和弯曲法。无论是拉伸法还是弯曲法,其关键所在都是要精确测量出材料在外力作用时,微小的形变量。目前,拉伸法多数借助光杠杆放大法测量形变[2-6]。但拉伸时物体通常存在弛豫过程,不能真实地反映物体内部结构的变化,而且实验中施力大小也不易把握。过小时不足以消除金属丝的弯曲,过大则有可能超出物体弹性限度。弯曲法多数利用读数显微镜测量形变,但读数显微镜是直接读取形变的,而且显微镜测量时容易产生回程误差[7-12],所以精度要低一些。若将拉伸法的光杠杆测量移植到弯曲法中就无须拉伸和用读数显微镜读取数据,这样既能避免材料拉伸时的一系列不利因素,还能消除显微镜读数时的一些误差隐患,具有扬长避短的效果。
2 光杠杆放大原理
放大法思想在物理实验中有着极广泛的应用。当实验中遇到需要对极微小的物理量变化进行精确测量时,通常采用放大法对待测量放大适当倍数,再进行精确测量,最后再按照放大原理的逆路径通过适当计算还原待测物理量[13-16]。常见的放大法有光杠杆放大法和薄膜干涉放大法等,其中光杠杆放大法是利用几何光学原理,故该方法有着原理通俗易懂,器材较少,平台易搭建等优点。如图1所示,光杠杆是一个有着三足的小平面镜。
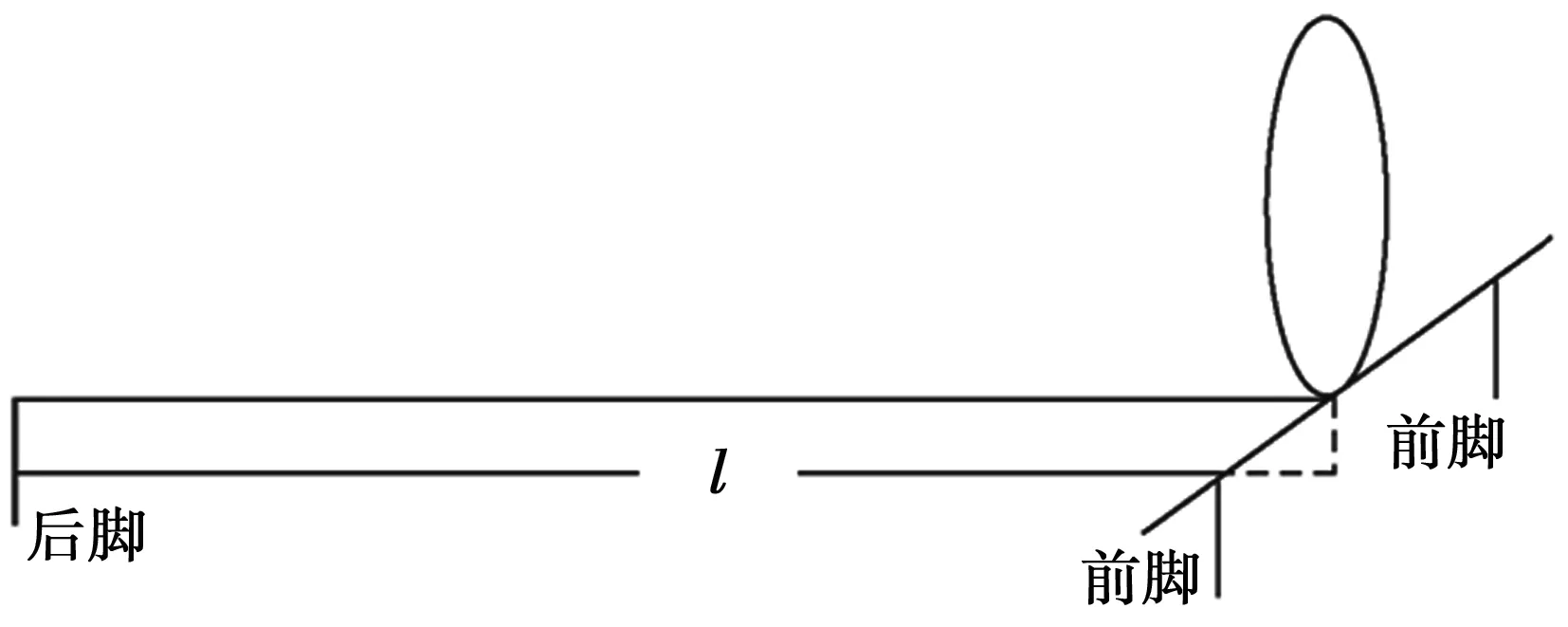
图1 光杠杆示意图
其中l尺寸可调节。实验中将光杠杆的两前脚固定,后脚置于待测物体上端。平面镜呈竖直状态,如图2所示。在平面镜的正对面较远距离D(D≫l)处放置一望远镜,望远镜侧面固定一标尺。通过调节望远镜的位置和焦距,可以在对面的平面镜里观测到标尺的反射像,并且可以读数。
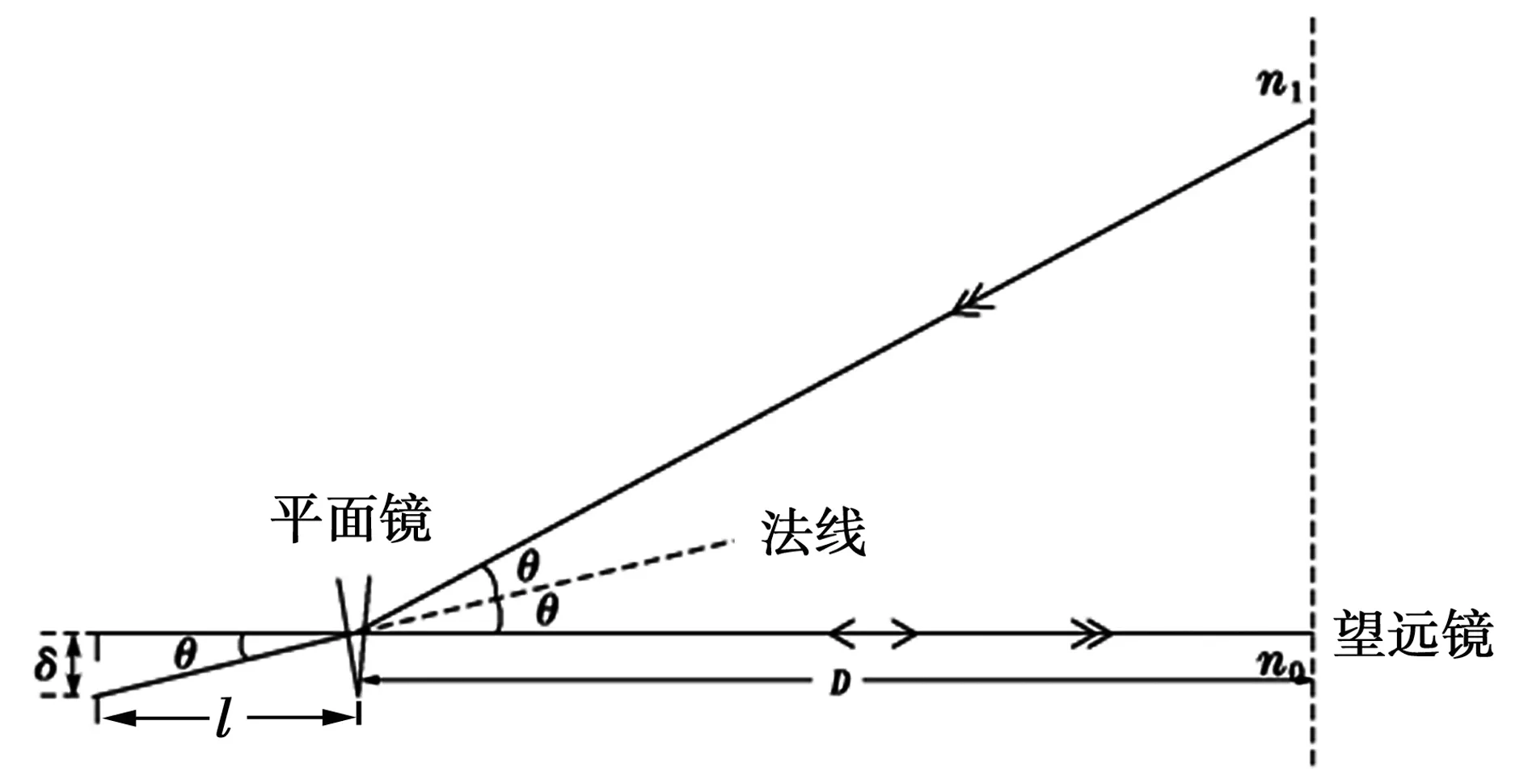
图2 光杠杆放大原理图
如果待测物体有略微形变(如下移),则会使光杠杆后脚以前脚为支点旋转一微小角度θ,镜面及其法线随之旋转相同角度θ。根据几何光学原理不难证明形变后的入射光线较之前旋转了2θ[8-10]。设形变为δ,结合装置参数及读数且考虑θ很小,则有:
(1)
(2)
联立(1)、(2)有:
(3)
3 杨氏模量测量
3.1 杨氏模量
如图3所示的是一根长为x的直棒,其截面积为s。若在其一端施加一作用力F后,直棒有了Δx的形变,则比值Δx/x称为直棒的应变,比值F/s称为直棒的应力。据胡克定律可知,在弹性限度内物体的应变ε=Δx/x与应力F/s成正比关系[15-18],即
(4)
式中比例系数Y即为物理学中定义的杨氏模量,它只决定于物体的材料,与物体的形状、尺寸及受力大小无关。
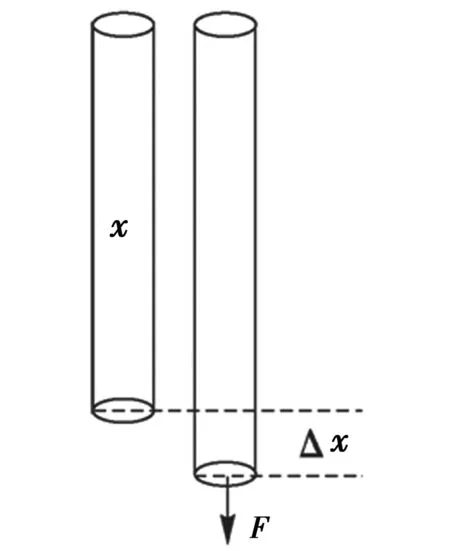
图3 拉伸形变示意图
3.2 弯曲法杨氏模量测量
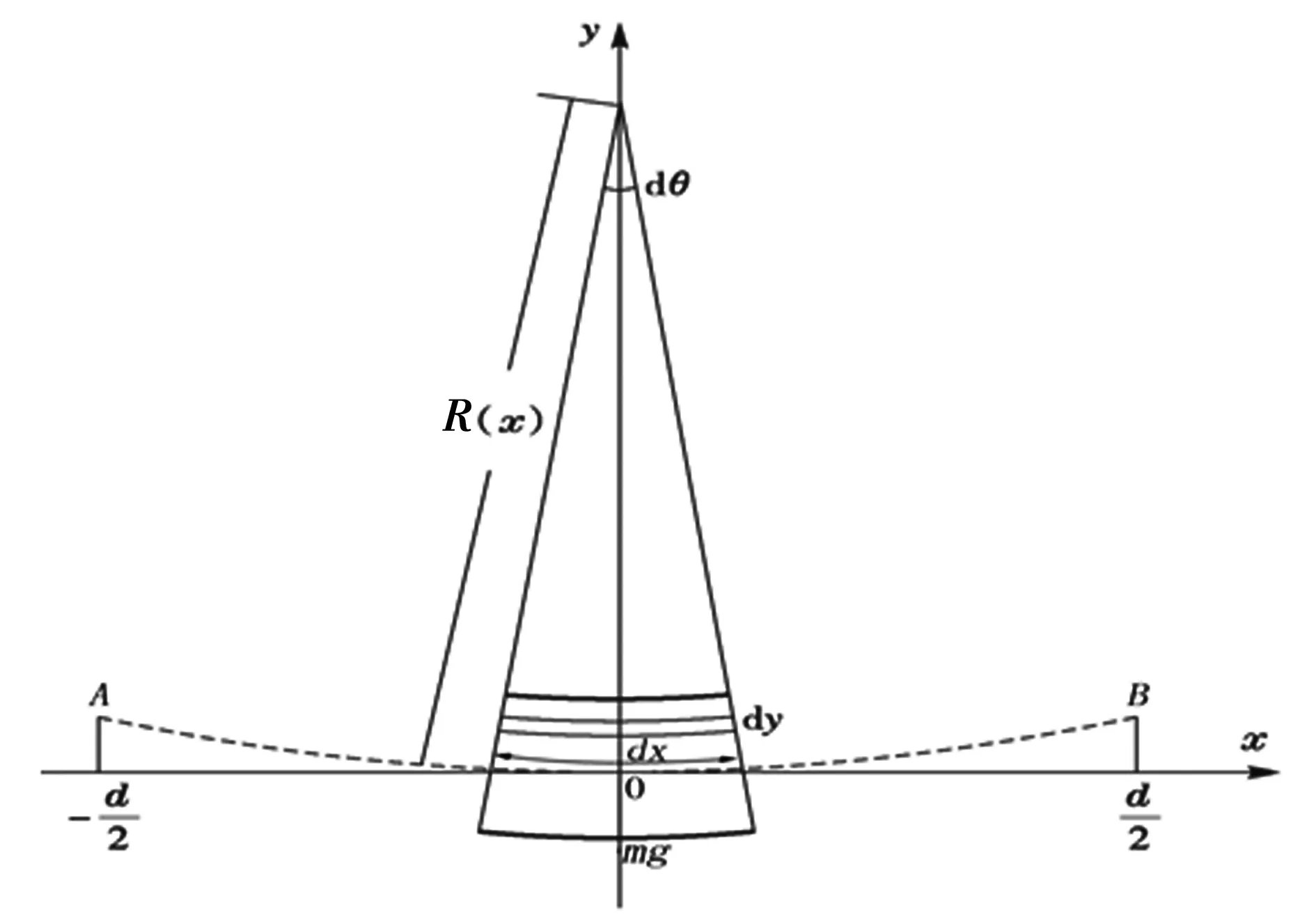
图4 横梁弯曲示意图
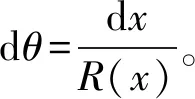
(5)
则据3.1所述内容应变ε为:
(6)
将(6)式代入(4)式得:
(7)
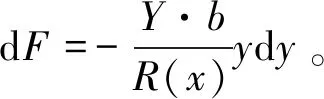
(8)
对整个横断面的转矩即为对(8)式积分:
(9)
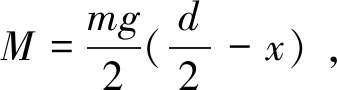
(10)
根据高数相关知识可知横梁上各点曲率k可表示为:
(11)
其中y(x)为横梁弯曲曲线方程。因横梁弯曲微小,故y′(x)=0,则(11)式可化简为:
(12)
将(12)式代入(10)式可得:
(13)
根据边界条件y(0)=0;y′(0)=0,解微分方程(13)得
(14)
(15)
实验中只要对下降的距离δ精确测量,再结合其他固定参数即可求出物体的杨氏模量Y。
3.3 基于光杠杆的弯曲法杨氏模量测量
根据3.1内容所述,测量物体杨氏模量Y必须对横梁下降距离δ做精确的测量。但δ很小,所以设计了光杠杆放大法对δ进行精确测量。
如图5所示装置是将光杠杆前两脚放置于固定台面,后脚置于横梁钩码之上,然后在光杠杆平面镜的正前方较远处(一般2米以上)放置带有标尺的望远镜,调整望远镜直至看清平面镜里标尺的反射像,并读取刻度n0。如图2所示。然后轻轻加挂砝码,此时会看见望远镜里标尺刻度会变化至n1,然后代入相关固定参数得出(3)式,最后将(3)式代入(15)式得出
(16)

图5 光杠杆法杨氏模量测量装置图
(16)式即是基于光杠杆的弯曲法测量杨氏模量的实验原理公式。实验中还可以多次加挂砝码并依次记录望远镜刻度值,然后采用如逐差法等数据处理方法来提高测量准确度[17-21 ]。
上述实验装置是在读数显微镜的平台基础上改建而成,利用了光杠杆的几何光学原理将微小的待测量放大后测量,相比较于薄膜干涉法等其他放大法而言,它的原理简单,器材较少,操作容易,容易推广。同时该平台有效规避了拉伸法及弯曲法中读数显微镜的不足[9-11]。
4 总 结
文中结合杨氏模量测量的两种常见的方法,对两种测量方式的优缺点进行了简单的分析对比,针对他们的优势与不足设计了一种新型的杨氏模量测量装置,该装置是基于光杠杆的弯曲法杨氏模量测量,是将光杠杆放大法与弯曲法结合起来的一种取长补短的测量方法。该方法巧妙地利用了几何光路图将待测物理量扩大,使测量变得更加准确,同时避免了读数显微镜直接读取δ时的视觉误差,及拉伸法中可能出现的待测钢丝与装置的摩擦等不利因素,再次提高了测量精确度;在实验原理设计过程中采用了简单的数学知识,从而化解了物理过程中弯曲角度与下降距离之间的抽象且晦涩的物理关系,便于对实验原理的理解。

