脉冲中立型随机微分方程的均方指数稳定性
徐 燕
河北大学数学与信息科学学院,河北保定,071002
最近几十年,中立型随机时滞微分系统受到学者的大量关注,因为该模型可以描述很多领域的一些随机现象[1],比如神经网络,种群生态学,化学工程仿真,计算机辅助设计,自动控制领域等,其研究热点是系统的渐近行为分析[2]。另外,脉冲效应存在于各种应用模型中,用于描述系统状态在某一时刻的突变。目前,脉冲中立型时滞微分方程已有很多研究结果,如文献[3]研究了一阶欧拉型中立型脉冲微分方程解的渐近行为,文献[4]研究了一类脉冲非线性中立型随机微分方程解的渐近性。许多物理系统经常遭受到不可预测的结构改变,例如机器突然失灵,瞬间的环境扰动等,在数学上经常用马尔科夫调制的系统来描述这类系统。2003年,Kolmanovskii等考虑了马尔科夫调制的中立型随机时滞微分方程解的存在和唯一性,并且研究了解了渐近有界性和均方指数稳定性[5]。尽管有很多文献讨论了脉冲中立型随机微分方程和马尔科夫调制的中立型随机微分方程的稳定性,但关于马尔科夫调制的脉冲中立型随机时滞微分方程指数稳定性的研究工作很少,如文献[6]利用Lyapunov方法结合线性矩阵不等式讨论了马尔科夫调制的脉冲中立型随机神经网络模型的均方指数稳定性。受此启发,本文利用文献[7]和[8]中的方法研究马尔科夫调制的脉冲中立型随机时滞微分方程的均方指数稳定性。
1 模型描述和预备知识
令τ>0,PC([-τ,0];Rd)={ψ:[-τ,0]→Rd|ψ(t-),ψ(t)存在,ψ(t+)=ψ(t),‖ψ(t)‖=

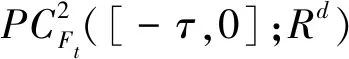
令r(t),t≥0是概率空间上取值于有限状态空间S={1,2,…,N}的一个右连续的马尔科夫链,它的生成元Γ=(γij)N×N满足
P{r(t+Δ)=j|r(t)=i}
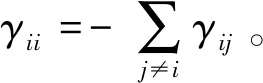
假设r(t)与布朗运动w(t)是相互独立的。r(t)几乎每一个样本路径是右连续的分段函数且在R+(:=[0,))的任何有限子区间上是有限简单跳。
记C2,1(Rd×R+×S;R+)表示所有定义在Rd×R+×S上关于x连续可微关于t连续可微的非负函数V(x,t,i)的全体。
下面讨论马尔科夫调制的非线性脉冲中立型随机时滞微分方程的均方指数稳定性:
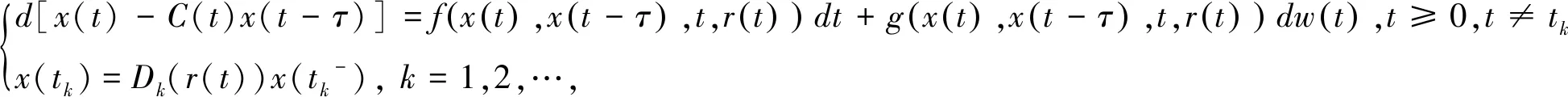
(1)
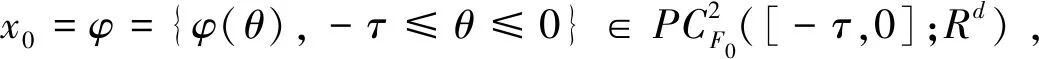
假设f,g,Dk满足解全局存在和唯一的必要条件,对于t≥0,记此唯一解为x(t,x0)。为了讨论稳定性,假设f(0,0,t,0)=g(0,0,t,0)=0和Dik(0)=0,k∈Z+,则系统(1)有一平凡解x(t)≡0。
一个随机过程x(t)称为系统(1)的解,若满足下列条件
(1) 当-τ≤t≤0时x(t)=φ(t),当t≥0,t≠tk(k=1,2,…)时x(t)是连续的;
(2) 当t≥0,t≠tk(k=1,2,…)时x(t)-C(t)x(t-τ)是连续可微的且满足系统(1);
(3)x(tk+)和x(tk-)存在且x(tk+)=x(tk)满足系统(1)。
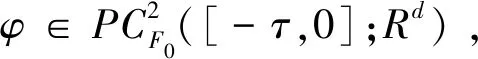
定义2[10]泛函V:Rd×R+×S→R+属于类Ψ0,若满足下列条件:
(1)泛函V在集Rd×R+×S上是连续的且当t≥0时,V(0,t,i)≡0,i∈S;
(2)V(x,t,i)关于x∈Rd,i∈S是局部Lipschitzian的;
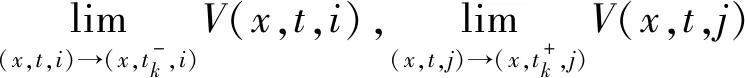
引理1[9]171设a,b∈Rd及0<ε<1。则下式成立
|a+b|2
(2)
引理2[8]设β>0,0
E|x(t)-C(t)x(t-τ)|2≤ce-βt,t≥0
(3)
则E|x(t)|2≤Ae-(β∧α)t
(4)
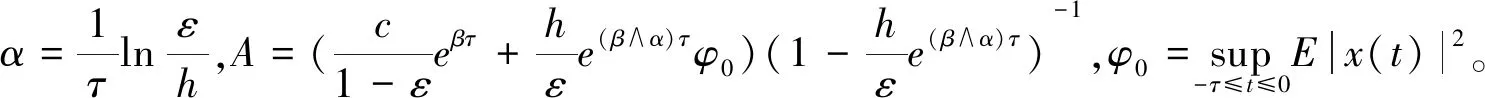
引理3[11]假设W∈Rd×d是正定矩阵,U∈Rd×d是对称矩阵,则对任何x∈Rd,下式成立xTUx≤λmax(W-1U)xTWx。
2 主要结果和证明
使用Lyapunov-Krasovskii泛函证明系统(1)的均方指数稳定性。为了讨论方便,当r(t))=l,记矩阵Dk(r(t))为Dlk。考虑系统(1)的脉冲时刻tk,假设tk-τ不是脉冲时刻且下列条件成立
C(tk)=Dk(r(t))C(tk-),k=1,2,….
(5)
定理1令β0是一个固定的正常数,假设对每一个i∈S,存在对称正定矩阵Ui,以及常数βi∈R,使得以下条件成立:
(x(t)-C(t)x(t-τ))TUif(x(t),x(t-τ),t,i)
Uig(x(t),x(t-τ),t,i)]
≤βi(x(t)-C(t)x(t-τ))T
Ui(x(t)-C(t)x(t-τ))
(6)
(7)
λmax(Ui-DikTUlDik)-1<0,r(tk)=l
(8)
则系统(1)的平凡解是均方指数稳定的。
证明:若V(x,t,i)∈C2,1(Rd×R+×S;R+),定义从Rd×Rd×R+×S到R的算子LV(x,y,t,i)=Vi(x-C(t)y,t,i)+Vx(x-C(t)y,t,i)f(x,y,t,i)
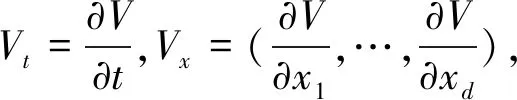
考虑下列Lyapunov-Krasovskii泛函:
V(x(t)-C(t)x(t-τ),t,i)=eβ0t(x(t)-C(t)x(t-τ))TUi(x(t)-C(t)x(t-τ))。 显然,V(x(t)-C(t)x(t-τ),t,i)∈Ψ0。当t∈[tk-1,tk),由系统(1)和引理3,得到:
LV(x(t)-C(t)x(t-τ),t,i)
=eβ0t{β0(x(t)-C(t)x(t-τ))TUi(x(t)
-C(t)x(t-τ))+2[(x(t)-C(t)
x(t-τ))TUif(x(t),x(t-τ),t,i)
TUj(x(t)-C(t)x(t-τ))}
≤(β0+2βi)eβ0t(x(t)-C(t)x(t-τ))
TUi(x(t)-C(t)x(t-τ))
≤(β0+2βi)eβ0t(x(t)-C(t)x(t-τ))
TUi(x(t)-C(t)x(t-τ))
进一步得到,
ELV(x(t)-C(t)x(t-τ),t,i)
其中x(t)=(x1(t),…,xd(t))。
则由(7)有ELV(x(t)-C(t)x(t-τ),t,i)≤0,t∈[tk-1,tk)
(9)
对任意的t,t*∈[tk-1,tk)且t>t*,应用Dynkin's公式,得到
EV(x(t)-C(t)x(t-τ),t,i)-EV(x(t*)-C(t*)x(t*-τ),t*,r(t*))

进而得到
EV(x(t)-C(t)x(t-τ),t,i)≤EV(x(t*)-C(t*)x(t*-τ),t*,r(t*))
(10)
当t=tk,应用条件(5)和(8),有
得到V(x(tk)-C(tk)x(tk-τ),tk,l)
≤V(x(tk-)-C(tk-)x(tk--τ),tk-,i)
(11)
应用数学归纳法,当i,l∈S以及k≥1,有
EV(x(tk)-C(tk)x(tk-τ),tk,r(tk))
≤EV(x(tk-1)-C(tk-1)x(tk-1-τ),tk-1,r(tk-1))
≤…
≤EV(x(0)-C(0)x(-τ),0,r(0))
(12)
联合(10)和(12),得到
≤EV(x(t)-C(t)x(t-τ),t,i)
≤EV(x(0)-C(0)x(-τ),0,r(0))
(13)
另一方面,由V(x(0)-C(0)x(-τ),0,r(0))的定义,我们有
EV(x(0)-C(0)x(-τ),0,r(0))
E|x(t)-C(t)x(t-τ)|2
因此,由引理2,得到E|x(t)|2≤Ne-(β0∧α)t,其中
最后,由定义1得出系统(1)的平凡解是均方指数稳定的且它的Lyapunov指数不超过-(β0∧α)。证毕。
3 例 子
为说明定理的应用,考虑下面一个二维马尔科夫调制的脉冲随机微分系统:
(14)
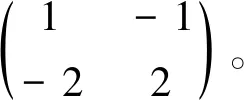
系统(14)的其他参数如下:t≥0,τ=2,
f1(x(t),x(t-τ),t,i)
f2(x(t),x(t-τ),t,i)
g1(x(t),x(t-τ),t,i)
g2(x(t),x(t-τ),t,i)
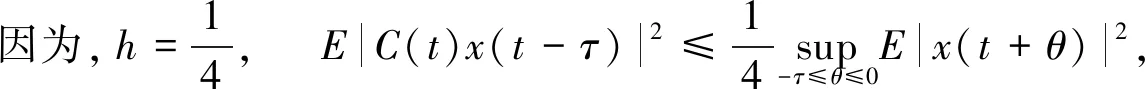
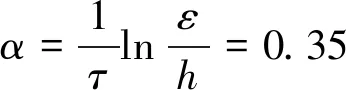
(x(t)-C(t)x(t-τ))TU1f(x(t),x(t-τ),t,1)
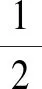
≤-1.5(x(t)-C(t)x(t-τ))TU2(x(t)-C(t)x(t-τ))
即,β1=-1,β2=-1.5。进一步计算得到
上面结果显示定理1的所有条件都满足。因此,由定理1,系统(14)是均方指数稳定的且Lyapunov指数不超过-(0.50∧35)。

