概率积分法开采沉陷预测的数值计算与分析

魏宗海，熊 伟

(河北省地矿局第三地质大队，河北 张家口 075000)

地下煤炭资源的开采会改变地质体平衡状态,进而引发地表沉陷问题[1]。由于煤层开采引起的地表沉陷预测在“三下”采煤、土地复垦治理等生产实践方面具有非常重要的作用，例如：在建筑物下采煤时，根据预测所得的结果可以判别建筑物是否受开采影响和受开采影响的程度，并依此作为对建筑物采取维修、加固、重建等维护措施的依据[2-4]；在铁路下开采时根据预计结果判断铁路下开采的可能性[5]；在水体下开采时，预计结果可以用来判断矿井受水患威胁的程度及开采对堤坝等设施的破坏和影响程度；在土地复垦工作中，根据预计结果可以确定地表塌陷的深度、范围和坡度等，并依此作为编制土地复垦报告的重要技术依据[6-7]。

目前，在我国普遍采用的开采沉陷预测方法是概率积分法，该方法已应用于大量的工程实践中，并积累了丰富的实践经验、形成了相对成熟的预测参数体系，而且有依据规范的指导，是当前常用的地表开采沉陷预测方法。由于该方法需要通过计算复杂的二重积分来获得地表开采沉陷值，人工计算过程繁琐且容易出错，对于多工作面、大范围地表沉陷预测更是难以实现。随着计算机技术的迅速发展，国内的不少煤炭研究院所和高校都开发了基于概率积分法的开采沉陷预测软件，其中具有代表性的有：中国矿业大学开发的MSPS软件、山东省鲁南地勘院开发的SODP软件、河南理工大学开发的MSDFVS软件以及山东科技大学、安徽理工大学开发的基于GIS的地表开采沉陷预测程序等[8-9]。这些软件的出现大大降低了沉陷预测工作的难度；另一方面，开采沉陷预测软件的编制必然要通过数值积分的方法来实现概率积分法中二重积分的计算，而数值积分计算必然会带来一定的计算误差，虽然地表沉陷预测的精度主要取决于预测参数的准确度，然而对于需要多工作面影响叠加来预测地表沉陷的情况而言，由于数值积分计算导致的误差通过累积会大大增加。因此，选择合适的数值积分方法来编制地表开采沉陷预测软件对提高地表沉陷预测的精度和预测效率都具有非常重要的实际意义。

目前对于概率积分法开采沉陷预测数值计算方法和计算精度方面的研究较少，针对这种情况，本文先根据概率积分法地表沉陷预测模型，提出了使用变步长辛卜生二重数值积分的方法对地表沉陷进行预测计算，最后结合一个工程实例对该方法的计算精度进行对比分析。

1 概率积分法开采沉陷预测方法

根据地表移动变形预计方法的建立途径，可以将其分为3类：基于实测资料的经验法、理论模拟法和影响函数法。概率积分法是影响函数法的一种，该方法以正态分布函数为影响函数，用积分式表示地表下沉盆地形态特征。在波兰学者李特威尼申创立的岩层移动随机介质理论的基础上，我国学者刘宝琛、廖国华提出了实用的概率积分法开采沉陷模型。

如图1所示，ABCD为某一缓倾斜煤层走向长壁工作面，工作面长为L1，推进长度为L2，工作面走向、下山和上山拐点偏移距分别为S0、S1、S2。在回采工作面下山建立如图1所示的计算坐标系，则对于地表任意一点P(x,y)，概率积分法开采沉陷预测值算式为：

(1)

Wc m=mq·cosα,

(2)

(3)

式中：W(x，y)为地表任意点P的下沉值，mm；m为工作面采厚，mm；q为下沉系数；为煤层倾角，(°)；r为主要影响半径，m；H0为工作面平均采深，m；β为主要影响角，(°)；u，v为开采单元在x，y方向上的坐标值，m。

图1 概率积分法开采沉陷计算示意图

2 沉陷预测的数值积分计算方法

2.1 数值积分原理

数值积分是用数值逼近的方法对给定的积分函数进行近似计算的一种方法。如果某一函数f(x)在区间[a,b]上连续且n+1阶可导，则f(x)可近似为该区间上n+1个结点的n次插值多项式Pn(x)，即：

(4)

那么，f(x)在区间[a,b]上的积分可近似为函数Pn(x)在区间[a,b]上的积分，即：

(5)

式中，ck为求积系数。式(5)表明，任意一个在区间[a,b]上连续且n+1阶可导的函数f(x)都可近似为该区间上某些结点处的函数值的线性组合。显然，取不同的n+1个结点，可以得到不同的插值求积公式，当n=2时，式(5)对应的求积公式即为辛卜生求积公式，即：

(6)

需要注意的是，对于取n+1个结点构造的求积公式有n次代数精度，即：对于所有次数不超过n的多项式来说，求积结果均准确可靠；而对于n+1阶多项式来说则不一定准确。

在计算二重积分时，可以将二重积分转化为两个一重积分的乘积，然后分别使用式(6)对一重积分进行计算，最后相乘即可得到二重积分结果。

2.2 开采沉陷预测的变步长辛卜生二重积分数值计算方法

根据上节介绍的数值积分原理，将含有二重积分的概率积分法开采沉陷预测公式表示为两个一重积分G(u)、T(v)的乘积，即：

(7)

(8)

由回采工作面开采范围可知，一重积分G(u)、T(v)的积分区间分别为[S1,L1-S2]、[S0,L2-S0]，由于直接使用式(6)在整个区间内对函数进行积分的误差比较大，因此，需要将整个积分区间划分为若干小区间，再在各个区间上分别使用式(6)进行求积，最后将各个区间的求积结果进行叠加，即可得到函数积分在整个积分区间的结果。在数值积分中，积分精度是一个非常重要的问题。一般来说，整个积分区间中划分的各小区间长度(积分步长)越小，积分精度越高；但是，如果步长取的太小，计算量则会大大增加，而且由于累加积分项数的增加，累积误差也会增大，进而会导致沉陷预测误差过大。因此，在实际计算中，通常根据计算精度要求逐步将积分区间进行二等分(即，变步长)。

以计算一重积分G(u)为例，在使用变步长辛卜生求积法时，首先将积分区间[S1,L1-S2]分为n(n=2)个小区间，则求积结果为：

(9)

式中，h为积分步长。然后，再分别将每个小区间划分为n个子区间，则有：

(10)

根据式(9)和式(10)构造辛卜生求积公式的积分结果为：

(11)

上述过程即为变步长辛卜生求积分方法的一个子计算过程。由于一个子计算过程往往不能对积分结果进行充分近似，通常情况下，需要不断重复上述过程，直到前后两次的积分值之差小于某一限制精度为止，即：

|S2n-Sn|<ε.

(12)

另外需要注意的是，为了防止积分步长无休止地划分下去，从而导致累积误差过大的现象发生，一般应对积分的最小步长加以限制；也就是说，当积分步长小于限制步长h0时，无论积分结果是否小于限制精度，都应停止运算，返回积分结果。

使用辛卜生变步长求积分方法计算开采沉陷预测值的算法可归纳为：

1)确定预测及计算参数。根据工作面地质采矿条件，确定积分区间范围、概率积分法预测参数；根据预测需要，确定预测点的平面坐标P(x,y)；根据计算精度要求，确定积分限制精度和限制步长。

2)计算预测点P(x,y)在x方向上的开采沉陷预测函数g(u)的积分值。

①根据x方向的积分区间划分数n计算步长h和积分值Zn；

②计算步长折半后的积分值Z2n，并构造辛卜生求积公式的计算结果Sn；

③重复步骤①、②，并判断前后两次积分结果(Sn，S2n)之差是否符合限制精度要求，判断当前积分步长d是否达到限制步长要求；

④若前后两次积分结果之差符合限制精度要求或积分步长达到限制步长要求，则返回积分结果。否则重复①～③的计算步骤。

3)计算预测点P(x,y)在y方向上的开采沉陷预测函数t(v)的积分值，计算过程与g(u)函数积分计算过程相同。

4)将x方向、y方向的积分结果G(u)、T(v)代入式(7)，获得P(x，y)点的开采沉陷预测值WP(x,y)。

该算法的流程如图2所示。

2.3 非标准坐标系的概率积分法开采沉陷预测

在实际开采沉陷预测中，往往需要使用矿山采掘工程平面图(如Autocad格式)作为底图进行地表沉陷的预计。一般来说，回采工作面在电子版采工图坐标系中是非标准存在的(如图3(Ⅰ)所示)，即：坐标原点不处于回采工作面倾斜方向与走向方向的交点；倾斜方向非x轴方向；走向方向非y轴方向。此时，为了使用前文所述的数值方法进行开采沉陷预测，就必须首先进行坐标系的变换，通过坐标平移和旋转的方法将工作面及预测点坐标转换到标准的计算坐标系统中，如图3所示。

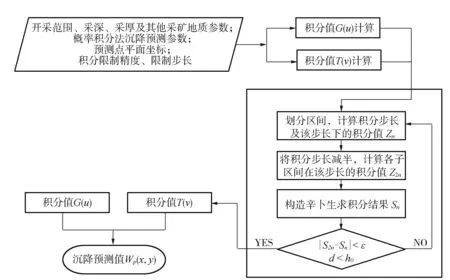
图2 辛卜生二重数值积分开采沉陷预测算法流程

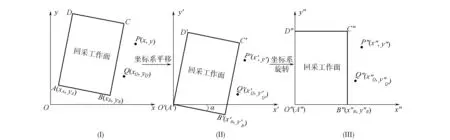
图3 坐标系变换示意图

设工作面倾斜方向与走向方向交点在原始坐标系O(xy)中的坐标为A(xA,yA)，则回采工作面角点坐标及预测点坐标(x,y)在平移后的坐标系O′(x′y′)中的坐标(x′,y′)为：

(13)

(14)

通过式(13)及式(14)将非标准坐标系下的工作面角点坐标及预测点坐标系转换为标准计算坐标系下的相应坐标后，根据工作面角点及预测点在标准坐标系中坐标、概率积分法预测参数及采矿地质参数，利用前文所述的变步长辛卜生数值积分方法进行开采沉陷预测。标准计算坐标下任意预测点P″(x″y″)的沉陷值WP″(x″,y″)即为原始坐标系下对应点P(x,y)的沉陷预计值。

3 实例与分析

某煤矿1300工作面为该矿一采区首采走向长壁工作面，工作面所采煤层为下二叠系山西组底部之3煤层；工作面于2006-11-21开始回采，2007-03-16停采；该工作面长246 m，实际推进长度606 m，煤层倾角4.8°，平均采厚5.5 m；工作面上山采深389 m，下山采深410 m，平均采深399.5 m。为研究该工作面所在采区地表移动变形规律，根据工作面井上下实际情况，在该工作面上方布设了2条地表移动变形观测线：一条全倾向观测线和一条半走向观测线，如图4所示。2006-09-05对两条观测线进行了首次全面观测，2008-11-27进行了最后一次全面观测；期间对2条观测线共进行了19次高程日常观测和5次平面日常观测。观测站全面观测、日常观测次数和精度要求均符合《煤矿测量规程》中的有关规定要求。

图4 工作面位置及测线布设图

根据该矿相邻矿井已有的地表移动监测资料，结合回采工作面地质采矿条件，确定该工作面概率积分法预测参数如表1所示。将变步长辛卜生数值积分的限制精度、限制步长分别设置为0.01和0.1，根据该工作面地质采矿参数和概率积分法预测参数对观测线各点进行沉陷预测。另外，为了验证文中提出的开采沉陷预测计算方法的准确性，同时使用MSPS软件对测线各点进行预测。文章提出的方法计算结果、MSPS软件计算结果和测线最后一次全面观测的实测数据对比如图5所示。需要注意的是，考虑到走向观测线各点和倾向观测线靠近1301工作面的Q9-Q13点受相邻工作面重复采动的影响，文中只对倾向测线上Q1-Q8点的实测下沉值与预测值进行比较。

表1 概率积分法开采沉陷预测参数表

图5 开采沉陷预测结果比对图

从图5可以看出，文中提出的方法和MSPS软件预测结果是非常接近的，走向测线、倾斜测线的提出方法与MSPS软件计算结果的标准差分别为12.3 mm、21.1 mm。造成这种差异的原因可能是MSPS软件中概率积分函数的数值计算实现方法与文中提出方法不同；也可能是由于MSPS软件也使用了文中提出的数值积分方法计算概率积分函数，但是软件中设置的限制步长和限制精度与文中设置的精度不同造成的。从倾向观测线上8个测点的实测数据来看，两种方法与地表实测下沉值之间存在较大的差异，这种情况主要是由于所取的概率积分法预测参数与该区域最优预测参数之间的差异造成的。文中提出方法的预测结果、MSPS软件预测结果相对于实测值的平均误差、标准差和均方根误差如表2所示。可以看出，提出方法的开采沉陷预测结果略优于MSPS软件的计算结果。另外，从上述结果来看，虽然由于预测参数不足够精确造成的误差占沉陷预测误差的大部分(最大误差28.5 cm)，但是由于积分方法造成的计算误差仍是一个不可忽视的因素(约1～3 cm)；特别是在大范围、多采区、多工作面预测时，往往是通过单独计算每个工作面的地表沉陷预测值，然后通过叠加的方法计算最终地表沉陷值，在这种情况下，各工作面的计算误差累积后可能会远超过由于预测参数不精确导致的误差。

表2 辛卜生方法、MSPS软件开采沉陷预测误差表 mm

4 结 论

文章提出了使用变步长辛卜生二重数值积分对概率积分函数进行计算，从而实现地表开采沉陷预测的方法；针对非标准坐标系下回采工作面的沉陷预测问题，文章提出了通过坐标系平移、旋转将非标准坐标系转换为标准计算坐标系下工作面开采沉陷预测的问题。通过实例计算和分析表明：

1)变步长辛卜生数值积分方法可以准确、可靠地对地表开采沉陷预测值进行计算；

2)基于变步长辛卜生数值计算方法的开采沉陷预测结果略优于MSPS软件计算结果；

3)虽然由于预测参数不足够准确导致的误差为沉陷预测误差的主要误差，但是由于积分运算导致的误差仍不可忽视，在开采沉陷预测中应尽量选择合适的数值积分方法，减小由于计算导致的沉陷预测误差。

虽然文中只探讨了基于概率积分法的地表沉陷数值积分方法，由于其它地表变形值(如倾斜、曲率等)的预测公式与概率积分法地表下沉值预测公式类似，文中提出的数值积分方法同样适用于地表倾斜、曲率、水平移动和水平变形预测值的数值计算。