基于GAMIT对国家GNSS基准站进行的北斗基线解算分析

刘洋洋，党亚民，许长辉

(中国测绘科学研究院 大地测量与地球动力学研究所，北京 100830)

北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)是中国具有完全自主知识产权研制的继美国全球定位系统(Global Positioning System, GPS)和俄罗斯卫星定位系统(Global Navigation Satellite System, GLONASS)后第3个成熟的卫星导航定位系统；美国的GPS系统自从上世纪建成以来，已经占据大半市场[1]；随着北斗导航卫星系统的逐步建立，已经向亚太大部分地区正式提供连续无源定位、导航、授时等服务，且在亚太地区，BDS较GPS能提供更好的定位服务，北斗系统在定位精度等方面不逊GPS系统[2-4]。

GAMIT软件是美国麻省理工学院 (Massachusetts Institute of Technology，MIT)与斯克里普斯海洋研究所 (Scripps Institution of Oceanography，SIO)共同研制的国内外公认的高精度数据后处理软件之一，由于其优良的解算特性，在国内外GPS数据高精度解算时得到广泛应用[5]，但是由于BDS与GPS系统在星座构型、坐标框架、时间系统。信号频率等方面有明显差异，GAMIT 10.6版本之前只能解算GPS数据，对于BDS数据不能进行有效处理[6]，国内学者自行利用算法程序进行北斗数据的处理，得到一些较可靠结论。文献[7]自行编制了北斗单历元定位算法程序，利用国内某城市变形监测数据进行处理。并与Track解算的GPS数据进行对比分析；文献[8]编制程序对北斗数据进行处理，与中海达TGO软件、天宝TBC软件和Bernese软件进行对比分析；文献[9-10]根据程序算法精确固定模糊度进而对北斗基线数据进行解算，也获得较好结果。但是这些文献所采用的分析方法均是自行编制的软件，且采用的数据质量难以评定，得到的结论缺乏可信度，本文采用GAMIT 10.61软件，对中国国家GNSS基准站的多系统观测数据进行北斗、GPS单系统数据解算，并采取自行编制的程序进行BDS/GPS组合基线解算分析，根据基线解算结果进行对比分析。

1 基线解算模型

高精度基线解算利用双差观测量建立误差方程，因双差观测组合可以消除接收机钟差、卫星钟差，削弱对流层延迟、电离层延迟、卫星星历误差，且保留载波相位的整周模糊度为整数，也能消去解算参数，缩短解算时间[11]，采用载波相位测量的观测值方程式为

(1)

根据式(1)进行单点定位，构造基线在观测值间求差并利用差分观测值进行相对定位[12-13]，观测方程为

(2)

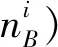
(3)

式中：P为伪距观测值；dX,dY,dZ为基线向量的坐标改正数；λ为载波频率的波长；l,m,n为3坐标方向上的方向余弦；Mp,ML为伪距和相位的多路径误差；εP,εL为伪距和相位的观测噪声。

2 算例分析

2.1 单系统基线解算分析

利用GAMIT 10.61版本，对国家GNSS基准站的4系统多频观测数据进行解算，分别进行单BDS/GPS的数据解算，解算日期为2017-04-10—2017-04-29共计20 d，选择测站分布均匀共75个站，站点分布见图1。解算设置观测值为LC_AUTCLN，解算策略选择BASELINE，截止高度角设置10°，设置采样间隔30 s，海潮模型选用FES2004，对流层映射函数设置为VMF1GRD.2017，大气潮汐改正模型、大气质量负荷改正模型设置为atl.grid、atmdisp_cm.2017，根据以下解算方案进行分析：方案1单独解算北斗系统的观测数据；方案2单独解算GPS系统的观测数据。

标准化的均方根误差(normalized root mean square，NRMS)表示解算出的单时段基线值与其加权平均值的偏离程度， NRMS值是衡量GAMIT基线解算质量的重要指标之一，计算式为

(4)

一般认为NRMS值应小于0.3，在0.25左右即可认为解算成功，否则需要检查原因，重新处理。若NRMS值大于0.5，表明基线解算是有问题的，可能性有未除去大周跳、某解算参数设置有问题、解算模型设定有误等情况。NRMS值越小，则代表基线解算的精度越高[14]，本次2种解算方案的基线解NRMS值结果见图2。

从图2可以看出，两种方案的所有解算天数的NRMS值小于0.25，满足解算要求，且解算效果较好；两种方案的NRMS值相差较小，从趋势上看来，方案2较方案1的解算效果更好，即在基线解算时，

图1 所选取测站分布图

图2 不同方案单天解基线NRMS值

GPS的效果略BDS较好，原因可能在于：测站接收的BDS的数据质量不如GPS、GAMIT对BDS系统数据解算添加的改正模型不如对GPS的改正效果精度高。

GAMIT采用双差观测量，在组合成基线解算时，会受到测站距离的影响，分析不同系统解算出来的基线长度均方差值(Root Mean Square,RMS)，将RMS值的变化量统计作为纵轴，横轴为基线长度，做升序排列，并将两方案结果对比，见图3。

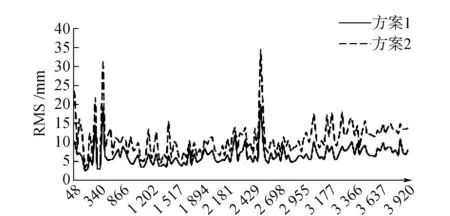
图3 不同方案解算的基线长度精度

从图3可以看出，方案1的基线长度精度明显不如方案2，即BDS单系统计算的精度略不如GPS单系统，但变化趋势一致，在明显的4处突变区域，都有较大反应；随着基线长度的增加，2方案的RMS值相差越大，说明，随着基线越来越来长，BDS的解算结果跟GPS结果差距加大；两种方案的长基线相对误差达到10-9，说明，即使BDS的基线长度解算精度不如GPS，但是也满足高精度要求的使用。

为了更加详细的分析解算单BDS和单GPS系统的数据结果，将基线的N，E，U方向做相对比较，且加上基线长的影响因子，以基线长为横轴，单方向中误差为纵轴，两方案在3方向的结果见图4。

从图4可以看出，方案1的3方向的基线精度均不如方案2，但随着测站距离的增加，方案1和2的精度变化趋势一致；N方向上，BDS系统数据解算质量不如GPS系统，中误差趋于一致，数值均值变化2 mm，BDS基线在南北方向精度6 mm，而单GPS系统较单BDS系统N方向中误差降低30%，且差值大的部分在基线较长的部分；E方向上，2种方案的精度差距较N方向精度差距明显，且不管基线长度，单BDS系统基线东西方向精度的结果均比单GPS系统中误差大4～6 mm，结果为10～12 mm，均值也是差5.1 mm，GPS的解算中误差较BDS系统降低42%，随着测站距离增加，BDS数据基线的突变也较多；U方向上，两种方案的精度都不是很好，这符合一贯的研究成果，高程方向的精度不如水平方向， 跟地壳的构造形变等因素有关[15]，此次结果中，GPS的U方向较BDS精度高，

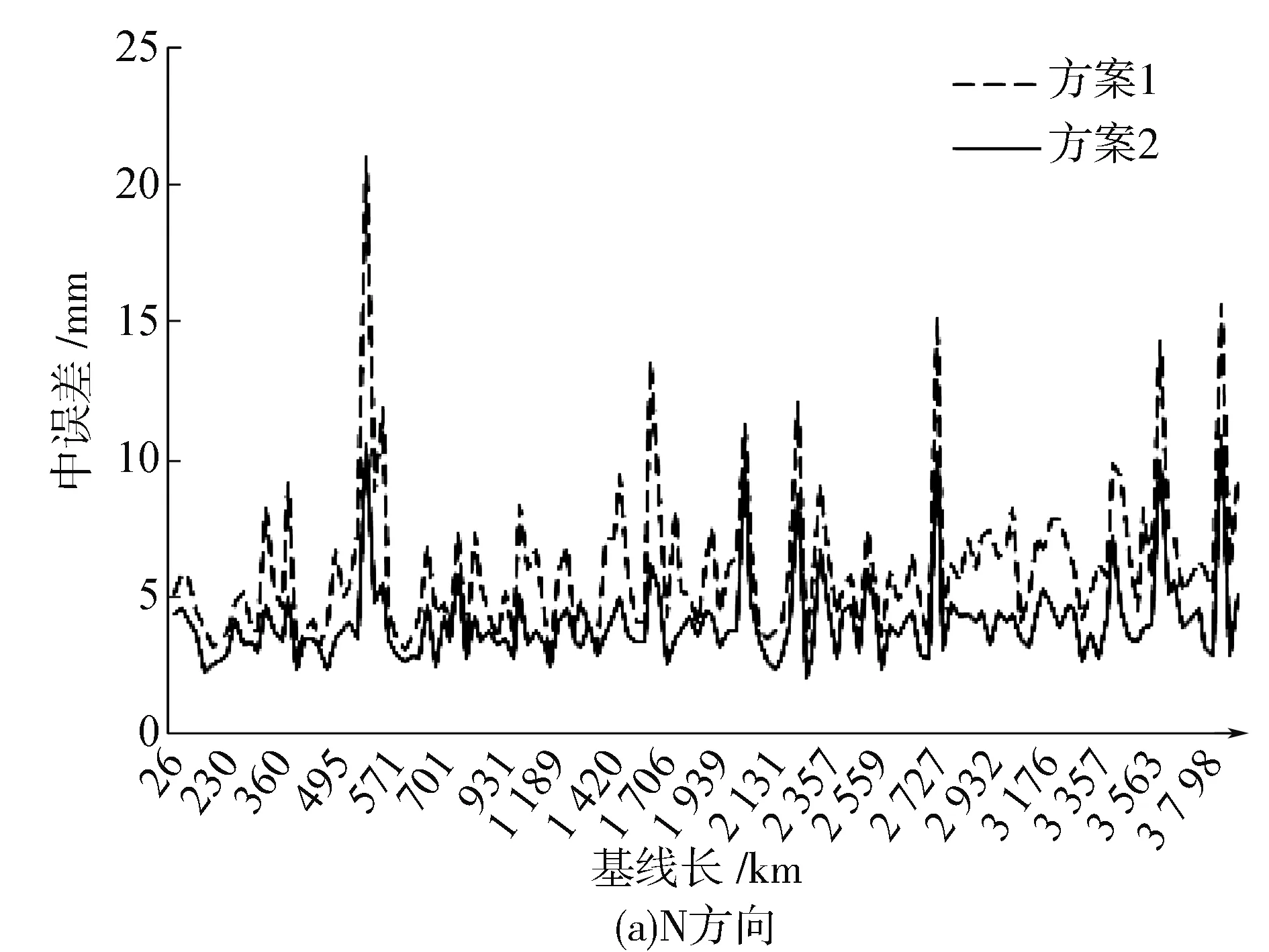
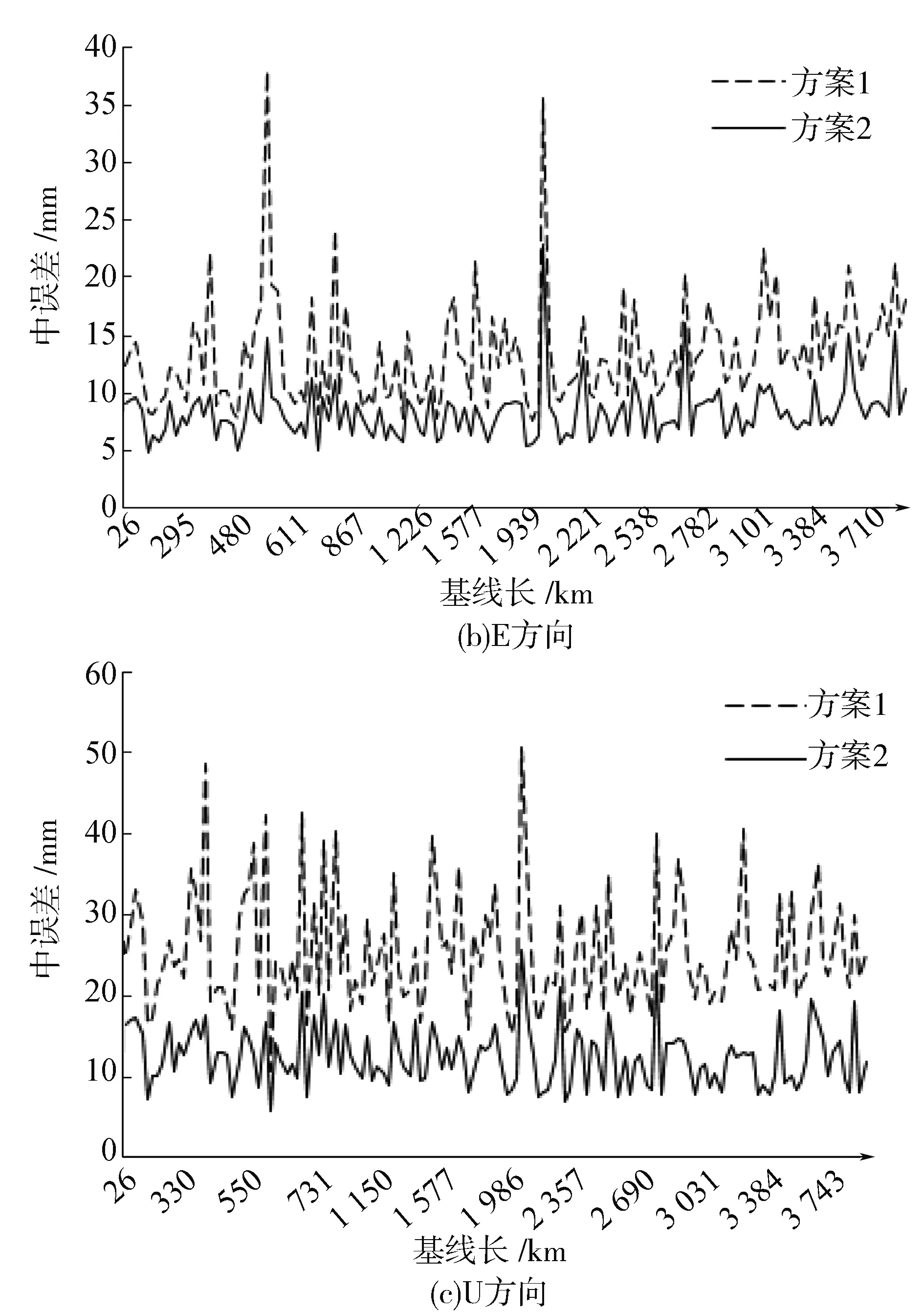
图4 基线单方向精度统计

且基线长度增加，并未给GPS数据解算带来较多突变，而BDS的中误差突变情况就较多，中误差均值为25 mm，大约是GPS系统中误差均值的2倍，反应目前BDS数据在高程方向精度较差，可能跟目前可观测到的卫星少、数据质量不稳定、改正模型精度不理想、受地壳形变因素干扰较大有关。

2.2 BDS/GPS组合系统基线分析

选取其中图1中所示测站进行BDS/GPS组合基线解算分析，由于GAMIT只能处理单系统数据，故此组合分析采取自行编制的软件进行测试。为避免不同软件之间处理数据出现的可能影响，故分别进行单BDS、单GPS、组合BDS/GPS基线解算试验，并分别从结果中选取其中几条基线解结果进行对比，如表1所示。

从表1可以看出，单BDS系统与单GPS系统的基线精度与图4中相差无几，水平方向精度基本优于1 cm，垂向精度1～2 cm，说明此次编写的程序可信度较好；BDS/GPS组合解算基线的精度较BDS系统有所提升，总体能优于1 cm，特别是高程方向，加入GPS系统后，可见卫星数目增大，有效提升了U方向精度。

表1 单系统与组合系统的基线解精度分析 mm

3 结 论

本文基于GAMIT10.61分别解算单BDS、GPS系统数据，通过对比分析基线解算结果精度，得出以下结论：

1)利用GAMIT解算BDS、GPS基线的NRMS值都较小，均能满足高精度解算的要求，基线的相对精度达到10-9，在工程或科研中，利用GAMIT解算BDS数据，完全可以满足精度需要。

2)BDS数据解算基线的南北方向精度6 mm，与GPS数据解算基线相差无几；BDS系统基线的东西方向精度10～12 mm，较GPS系统数据中误差增加42%，且存在突变情况；BDS系统基线的高程方向精度25 mm，且随着基线长度的增加，中误差存在较多突变发生，而GPS基线高程精度约为13 mm，存在较大差异。

3)组合BDS/GPS系统的基线解，提升单BDS系统的精度，特别在高程方向，精度优化1 cm左右。

4)由于GAMIT软件此前一直仅支持解算GPS数据，所以在新版本中可能对BDS数据解算时，加入的模型或卫星信息不是完全如GPS系统的精确，造成基线水平方向、高程方向的差异，而国内一些高校和研究院所自行编制的解算BDS数据的软件，能达到更好地解算精度，如何提高利用GAMIT解算BDS数据也是未来值得探讨的课题。