附加正交函数拟合条件的导航滤波方法

刘国良，蒋廷臣，喻国荣，潘树国，张 建2,

(1.淮海工学院 测绘与海洋信息学院，江苏 连云港 222005; 2.南京康帕斯导航科技有限公司,江苏 南京 210096; 3.东南大学 交通学院,江苏 南京 210096; 4.东南大学 仪器科学与工程学院,江苏 南京 210096)

随着无人机、共享单车、滴滴打车、无人驾驶汽车等大众导航新兴产业的发展，对于利用全球卫星导航定位技术实现米级至亚米级导航定位的需求正日趋旺盛。在大众导航领域采用的GNSS接收机大都是价格低廉、功能单一、数据质量不稳定的单频接收机。当这类接收机短暂经过城市高楼、高架桥、高大绿化植物时，卫星信号会被反射、遮挡或衰减，使得过街精度因子[1]快速恶化，导致接收机的定位结果往净空条件好的一侧偏移。

对于遮挡环境中，过街精度因子受到影响的问题，颜瑜军[2]基于3D建筑模型提出SM 与GPS组合的定位算法。王励扬[3]等利用车轮进动信息将DR系统与GPS系统组合，在信号遮挡时也能得到连续可靠的定位。欧敏辉[1]利用惯性导航不受净空环境干扰的特点，验证GPS/INS组合导航定位算法，使得过街平均误差提高到1.49 m。刘志锋[4]等通过电子罗盘和低精度IMU，融合航迹推算与合成孔径等技术实现障碍物遮挡环境下的动态定位。但是此类组合算法加入其他测量设备，极大地增加硬件成本，难以满足低成本的大众导航现实需求。因此，一些学者提出通过附加约束条件的方法从软件层面进行优化，常有附加迹向约束[5,6]，附加基线约束[7]、附加速度约束[8]的卡尔曼滤波算法等。附加迹向约束是基于载体运动时一般不会偏离航向的假设，通过现有地图或已知的道路航向构建约束条件，缺点是需要提前获知准确地迹向信息。附加基线约束通常是利用两个或多个天线间相对距离始终保持固定而建立约束方程，这种约束条件较为准确，且实用性较强，但也在一定程度上增加硬件成本。附加速度约束是通过载波或多普勒观测值解算得到的速度及方向，从而建立下一历元的运动约束条件。附加速度约束是目前比较经济可靠的方式之一，不需要通过外加硬件或先验信息而增加成本，但其仍然容易受到观测环境的影响而造成滤波不稳定。

为此，本文提出在速度约束的基础上增加状态拟合约束的抗差自适应滤波方法。该方法充分利用载体稳定的运动信息，通过采用正交函数最小二乘拟合的方式预测载体运动状态，从而形成新的约束条件，以增强单一速度约束滤波的稳定性。同时，为抑制不良观测值和运动模型误差的影响，加入抗差估计和自适应调节策略，利用速度条件和运动状态拟合条件联合建立抗差自适应卡尔曼滤波模型。

1 约束卡尔曼滤波模型

卡尔曼滤波是一种具有很高计算效率的实时参数估计方法，常用于导航定位算法当中。在实际的导航应用中，不仅速度，还有很多潜在的信息也能作为卡尔曼滤波的输入，文献[9]和[10]通过融合多个约束条件推导约束卡尔曼滤波模型。

假设卡尔曼滤波系统状态方程和观测方程为：

(1)

式中：下标k代表当前时刻；Wk为状态输入噪声；Γk-1为系统噪声驱动矩阵；Xk-1为前一时刻的状态估值；Φk,k-1为状态转移矩阵；Xk为当前时刻的状态向量；Lk为观测向量；Ak为设计矩阵；ek为观测噪声。假定观测值独立且系统噪声与观测噪声是互不相关的零均值高斯噪声。若附加约束条件为：

Dk=BXk+εk.

(2)

式中：设计矩阵B为时不变的单位阵，有时为rk×m维时变矩阵Bk,Dk是约束值矩阵，其协因数阵为Rk；εk为约束条件的噪声。当εk=0代表约束条件准确可靠为强约束，否则εk≠0。因此，由式(1)、(2)可建立拉格朗日最优化条件：

(3)

(4)

(5)

上式即为约束卡尔曼滤波模型。该模型由两部分构成，第一部分为标准卡尔曼滤波过程；第二部分为对标准卡尔曼滤波加以约束修正过程。

当Lk存在不良观测值和系统状态模型存在误差时，可按等价权原理对不良观测值作抗差估计和采用自适应因子调节模型误差的影响。即式(4)和式(5)的第3式可改写成附有约束条件的抗差自适应滤波模型。

(6)

2 正交函数的最小二乘拟合

在实际的导航定位中，当载体短暂经过高大建筑物时，常规最小二乘估计得到的定位结果会大幅偏移，若仅利用上一时刻精度不高的位置及速度估值去约束下一时刻的运动状态，一者容易造成基于速度建立的运动模型不准确，二者若在下一时刻也未观测到良好的卫星信息，未能及时对滤波模型做出准确地纠正，仅以速度约束的卡尔曼滤波模型的稳定性会容易受到扰动。对于机动性不高的载体，其运动轨迹、速度及航向的变化一般为直线或规则曲线，即下一时刻的运动状态，与之前若干时刻的运动状态间能构成直线或规则曲线等模糊依存的关系，且这种关系是呈现倒逆衰减趋势的。在数据处理中，建立这种模糊的依存关系常采用数据拟合的方法。在实际运用中，通过多项式进行拟合常采用正交多项式做最小二乘拟合[14]的方法。这种拟合方法采用递推公式，是目前进行曲线拟合的最好方法[15]。

假设各多项式函数{P0(x),P1(x),…,Pn(x)} (0,1,…,n为多项式次数)是满足：

(7)

若Ak=1时为标准正交函数系，对于给定节点{x0,x1,…,xm}求得离散正交多项式{P0(x),P1(x),…,Pn(x)}(n≤m)为

(8)

其中

(9)

因此，由最小二乘导出的方程组为：

(10)

解得系数{a0,a1,…,an}，则拟合函数为：

φ(x)=a0P0(x)+a1P1(x)+…+anPn(x).

(11)

由状态估值y求得拟合残差平方和均值为：

(12)

3 实测数据分析

在市区道路动态定位中，高大构筑物间断性地出现，因此信号遮挡亦为短暂性、间歇性的。此时若利用载波进行定位需要频繁初始化固定模糊度，实用性不强，而码伪距无须固定模糊度，且定位算法简单，对接收机硬件要求也不高，较符合大众导航领域米级至亚米级的定位需求。因此，本文采用GPS L1频点和BDS B1频点的码伪距观测值作为基础定位数据源。

3.1 遮挡环境影响分析

为直观重现卫星信号被短暂性、间歇性遮挡所造成的影响，采用某CORS站年积日为8d GPS 02:29:50～23:59:59的Trimble Net R9接收机采集的静态观测数据进行分析，在某观测质量较好的时段内，随机取120组连续10个历元剔除方位角在0°～180°的卫星数据，模拟实际间歇性遮挡环境。其中CORS站坐标参考值由GAMIT联合同期IGS站数据获得。周积秒为103 010 s时的全部可见卫星视图如图1(a)所示，遮挡后如图1(b)所示。

从图1可见，遮挡前可视卫星空间分布良好，遮挡后分布重心偏西南方向。采用单历元伪距单点解算间歇性遮挡前后数据并与参考值作差，相对应的平面定位误差分布如图2(a)、2(b)所示。

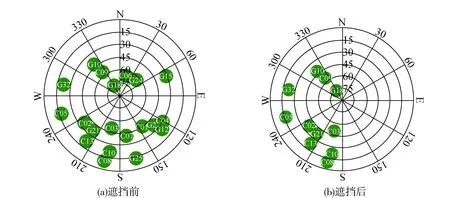
图1 周秒为103 010 s时星空图

图2 平面定位偏差

从图2(a)中看到，间歇性遮挡前伪距单点定位偏差在±1.5 m且分布均匀，表明在此测段内卫星观测数据质量较好。从间歇性遮挡后的图2(b)可见，未被遮挡的历元定位结果正常，被遮挡的历元有大幅度跳跃性偏移，N方向最大偏移量达10 m，偏移方向在卫星密集分布的西南方。为更直观显示各历元的实际偏移情况，绘制间歇性遮挡前后各历元在E方向的定位偏差，如图3所示。

从图3(a)可以看出，间歇性遮挡前N方向的定位偏差在±1.5 m左右，而图3(b)显示所随机选取的多组遮挡历元N方向的定位出现大幅度偏移，最大偏移量将近10 m，而未被选中遮挡的历元定位偏差仍在1.5 m之内。由此说明，当可视卫星被遮挡，导致空间分布不佳时会使解算结果出现大幅度的偏移。

除了遮挡之外，由高楼反射引起的多路径效应也会使定位结果出现不同程度的偏移。但无论是可视卫星分布不佳还是多路径效应的影响，在低成本的大众导航领域常是采用增加约束的方法予以抑制。

3.2 解算方案设计

为了验证本文所提方法在大众导航领域中的应用效果，采用集成Ublox-m8t芯片的单频GNSS接收机，采集多组动态实测数据。通过采集的码伪距观测值作基础定位，以3种解算方案进行解算分析：

方案1：伪距单点定位。采用经典最小二乘的参数估计方法。

方案2：速度约束的伪距单点定位。在方案1的基础上，采用多普勒求得的速度估值，建立匀速运动CV模型[9]，同时加入抗差等价权IGG-III方案，并采用两段函数法确定自适应因子，联合码伪距建立抗差自适应卡尔曼滤波模型。

方案3：拟合约束的伪距单点定位。在方案2的基础上，建立状态拟合+速度约束的抗差自适应卡尔曼滤波定位方法。

3.3 动态测试分析

第1组：在推行的自行车上简易安装ZHD-H32接收机和单频GNSS接收机。具体路线如图4(a)所示，接近终点的遮挡路段定位结果如图4(b)所示。

在图4(a)中，路线起点为天桥，随后转入半边有绿植遮挡的人行道，沿着地面近似直线的标识线推行至终点。图4(b)为第1 166～1 239个历元各方案的定位结果。从图4(b)中可以看出，当接收机经过遮挡信号的高楼时，伪距单点定位结果最大偏移约达30 m，过街精度极差，而基于速度约束的定位结果在一定程度上减少偏移量，但是拟合约束的改善效果更佳，定位结果更为平滑稳定。为直观表明拟合约束的改善效果，把速度约束和拟合约束的解算结果与参考值做差，绘制偏移明显的E方向差值如图5所示。

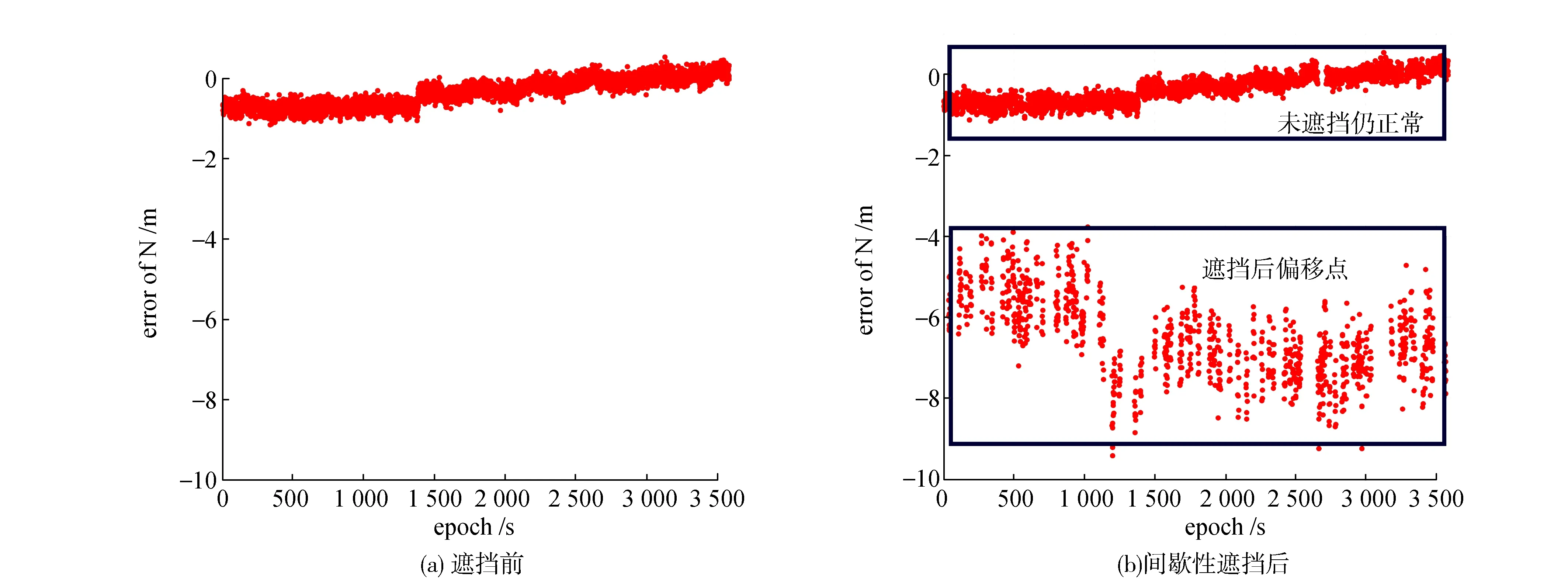
图3 N方向定位偏差

图4 第1组动态测试

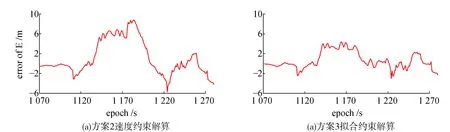
图5 第2组动态测试E方向偏差

从图5(a)中可以看出，仅附加速度约束的滤波结果通过抗差处理和自适应调节，在一定程度上削弱不良观测值的影响，使伪距单点约30 m的偏移量缩小到8.75 m；在图5(b)中，本文所提的拟合与速度联合约束滤波方法，把最大偏移量缩小到4.34 m左右，相较于方案2提升了50.4%，进一步增强滤波的稳定性。

第2组：在SUV越野车上装载毫米级 IMU/GNSS融合定位的GNSS终端动态检测设备和单频GNSS接收机，两者共用同一接收天线。通过Inertial Explorer软件解算IMU/GNSS采集的数据，以其解算结果作为参考值。由检测设备的定位结果绘制的行车路线如图6所示。

图6 行车路线

从图6可见，路线经过高架桥底、山边公路、隧道以及市区楼房等，基本穿越城市各类遮挡物边沿。截取其中一处高楼遮挡严重的Google Earth图像，如图7所示。

图7 第2组动态测试遮挡路段定位对比

在图7中，道路南侧有遮挡高楼，北侧有遮挡楼房，北侧影响较南侧严重。此时，伪距单点定位结果往南侧最大偏移达22.27 m，仅加速度约束的定位结果最大偏移量缩小到8.27 m，拟合与速度联合约束的进一步缩小，最大偏移量为5.78 m，较伪距单点提升74.0%，较速度约束提升30.1%。另外，分析全程(除隧道外)拟合与速度联合约束定位结果与参考值的偏差，统计结果如表1所示。

表1 拟合约束结果偏差统计表 m

从表1可以看出，即使在城市复杂道路环境下，本文所提方法在N，E方向仍能达到97%以内的定位精度。另外，需要注意的是，测试发现当接收机长时间处于可视卫星空间分布不佳的遮挡环境中时，若仍做机动性拐弯或小半径变道，附加拟合约束的定位结果会存在一定程度上的偏差。

4 结束语

本文通过实测数据分析在可视卫星空间分布不佳的遮挡环境中，定位结果会出现大幅度的偏移，通过采用增加新约束条件的方式以缩小定位的偏移，利用最小二乘正交拟合的方法，利用的拟合约束条件以增强卡尔曼滤波的稳定性，改善短时不良观测环境对定位所造成的偏移影响。从上述分析结果可以看出：

1)在高楼林立的城市道路观测环境中，卫星信号常受遮挡，可视卫星空间分布不佳，是使定位结果出现大幅度偏移的主要因素。此时若采用单历元伪距定位的方法会出现跳跃性的偏移，但通过增加约束的方法能够在一定程度上削弱遮挡环境的影响。

2)从各解算方案可以看出，附加拟合约束的定位效果最好，仅以速度约束的定位效果次之。从实测数据解算的最大偏移量看，附加拟合约束的定位效果比速度约束的提升30.1%以上，表明本文所提方法具有一定程度上削弱和大幅度偏移，增强滤波稳定性。

3)在实践中，通过拟合来建立约束条件也存在一些困难，如拟合窗口的宽度一般难以预先准确设定。在测试中试过m=5,10,15,20,35，其中m=10时效果较好。另外，通过拟合建立的约束条件并不能总保证其准确性，在观测环境良好时可不启用，拟合的多项式次数可按实际情况设定，文中采用的是二次多项式。

同时，本文所述的方法并未能完全消除遮挡、多路径和不良观测值的影响，仅是在一定程度上抑制偏移量，提高过街精度。当载体在遮挡环境下，还需采用惯导、激光、雷达以及视觉SLAM等辅助测量手段以进一步提升定位的稳定性及可靠性。