江北机场高填方夯后碎块石土剪切力学性质研究
马 昊,黄 达,2,肖衡林,王俊杰,马文浩
(1.重庆大学土木工程学院,重庆 400044;2. 河北工业大学土木与交通学院,天津 300401;3.湖北工业大学土木建筑与环境学院,湖北 武汉 430068;4. 重庆交通大学国家内河航道整治工程技术研究中心,重庆 400074;5. 空军航空大学,吉林 长春 130022)
山区机场大规模填筑工程填料大多就近或就地取材,填料多为岩体爆破得到的超大粒径块石夹碎石料,其物质组成不同于一般填土体。如重庆江北机场第3跑道高填方工程填料主要为砂岩、泥岩及少量黏土的碎块石土,其中泥岩经强夯后演变为泥质胶结物,夯后地基富含大粒径碎、块石(最大粒径甚至大于80 cm)。本文将这类填料称为碎块石土填料。目前已有多起高填方边坡大规模变形失稳的案例[1~3], 此类高填方边坡的稳定性受填料的剪切力学性质控制[4]。
鉴于碎块石土含有较多大尺寸块石、其结构极其不均匀性的特点[5],采用传统的室内试验难以获得相应的力学特征[6]。野外大尺度原位试验是揭示这种高度非均质复杂地质介质力学特性的一种有效办法[4]。李晓等[4]通过23 个大尺度原位推剪和压剪试验,较为系统地研究了土石混合体的剪切力学性质。张晓健等[6]对泥质页岩-粉质黏土混合填料进行了12个原位大型水平推剪试验,将土石混合填料的水平推力-位移曲线划分为压密、裂隙内部开展、裂隙贯通、剪切带形成、破坏后 5 个阶段。虽然原位试验较适用于土石混合料这类非均匀体,但超粒径颗粒的存在,使得将常规原位剪切试验运用于其参数取值时存在诸多问题[7]。近年来,已有部分学者利用特制设备进行了土石混合体大型室内试验研究,如夏加国等[8]对含超径颗粒的土石混合体进行了大型三轴剪切试验研究,胡峰等[9]基于大型直剪试验对土石混合体剪切带变形特征进行了试验研究。原位和室内大尺寸物理试验虽能较好地反映其真实力学特性,但试验结果随机性较大,成本高昂,局限性较大,可重复性差,难以广泛推广[10]。
碎块石土力学性质的试验技术及理论还有待发展,巨粒组颗粒粒径和试验设备尺寸的矛盾短时间内无法克服。本文采用现场大型探槽拍照及取样、图像处理、颗粒筛分、力学试验及数值模拟方法,依托重庆江北机场高填方工程,以剪切力学性质测试为例,提出一种新的碎块石土力学性质获取思路。
1 工程背景
1.1 地质条件及高填方边坡概况
重庆市江北机场第三跑道(T3)扩建工程所在场区地貌受构造剥蚀影响,为浅丘斜坡地貌,地面原始标高235.70~426.41 m,整体地势中、西部高,北、东、南侧低。岩性为侏罗系中统沙溪庙组(J2s)砂质泥岩、泥岩、砂岩,岩层呈单斜构造,产状15°~56°∠18°~27°。其中场区南部为岭状丘陵地貌,原始标高276~363 m,沟谷切割较深,岩层倾角较陡(25°~40°),地形起伏大,溪沟发育,沟底多覆盖第四系粉质黏土,两侧斜坡基岩出露,坡角15°~30°。
第三跑道(T3)场地平均地坪标高约400 m,原地形各地貌单元间高差达120 m,最低处标高仅235.70 m。整个施工区如图1所示,挖填方总量约7.533×107m3,填方边坡高度普遍在60~120 m,属于超大规模的超高填方边坡[11]。

图1 重庆江北机场T3填筑工程Fig.1 The fill project of the Jiangbeiairport (T3) in Chongqing
1.2 填料基本特征
本期扩建工程填料多来自场地内拟建航站楼及北侧毗邻地块的挖方区,总开挖量约6.1×107m3,填料岩性主要为砂质泥岩、砂岩、泥岩。挖方施工主要采用钻爆法。破碎岩块粒径差异较大且形状不规则,少量块石最大块径接近2 m。采用强夯法填筑施工,每堆填1层(单层厚度4 m)点夯1遍,在最后一层强夯填筑层点夯后进行满夯。
2 夯后填料级配特征
2.1 级配信息提取方法
《土的分类标准》[12]约定巨粒组土粒粒径范围是d>60 mm。对于填料中巨粒土组分,本文首先对夯后填土开挖探槽(槽深为单层强夯厚度),并在探坑垂直壁上摆放十字标尺,然后通过正面拍照获得高清夯后填土照片。运用Photoshop软件对探槽断面照片进行二值化处理,进而通过Matlab编程提取石块二值图像的像元坐标与灰度值及边界(图2)。并通过像元间距与真实尺寸的比例关系换算出巨粒组颗粒的真实尺寸。

图2 夯后填土巨粒边缘轮廓提取Fig.2 Extraction of giant grained rock blocks infill after dynamic compaction
对于粒径d<60 mm中小粒径土石料进行标准筛系筛分。共取15份料样,按取样探槽编号分5组,每个探槽内等深度间隔共取3份土样。将同一探槽内3份土样各粒组质量相加,得到各个探槽土样的级配曲线。
2.2 级配特征
共统计了5个探槽内的8个典型断面,图3为填料颗粒级配曲线,其中粒径大于60 mm的碎块石为图像识别结果(图3a)而粒径小于60 mm的土体为筛分结果(图3b)。探槽断面出露的块石最大粒径约1 000 mm,各断面出露的碎块石含量差异较大,部分粒组有缺失。

图3 夯后填料级配曲线Fig.3 Grain-size distribution curves of fillafter dynamic compaction
根据8个断面的粒径分布,将填料进一步分为三类:
富含大块石类(A类):中—大粒径含量较多且无粒组缺失,粒径d>60 mm的质量含量超过35%, 如断面2,6。
含大块石且级配不连续类(B类):断面1,3,5级配曲线局部有平台,中粒径块石存在明显缺失,级配不连续。
缺失大块石类(C类):无大块石(d>800 mm),粒径d>60 mm的质量含量小于25%,如断面4,7,8。
由图3b可知,探槽1,4,5(第1组)和探槽2,3(第2组)的碎石土级配曲线分别相近。对比2组试样的筛分结果,第2组的碎石土试样粗砾(20 mm 分别选取三类代表性夯后碎块石土的典型分布断面进行颗粒流模拟(表1),断面信息采集区长3.2 m,宽2.1 m。 将夯后土石混合料简化为石块和土体胶结料两部分,Medley[13]提出了二者的分界粒径为: d0=0.05Lc (1) 式中:d0——分界粒径; Lc——试样的工程特征尺寸。 本文信息采集区为矩形框,Lc可取短边2.1 m,由式(1)可得,分界粒径约为0.11 m。基于前面级配研究及相关土体粒径分级标准,采用分界粒径为60 mm,其值小于110 mm,符合要求。 3.2.1直剪试验模拟 采用PFC2D对填料进行直剪数值试验。分别使用颗粒单元和墙单元(wall)分别模拟试样和剪切盒(图4)。以下部剪切盒为主动剪切盒,由1#,2#,7#,8#墙体围合而成,试验时以0.1 mm·min-1向右运动;上部剪切盒在剪切过程中保持不动,由3#,4#,5#,6#墙体构成;通过Fish语言编程实现对5#墙体的伺服控制,以维持法向应力恒定。试验时法向应力取200,400和800 kPa 3个水平。 3.2.2填料离散化及接触模型选取 填料颗粒流模型的建模步骤如下:(1)通过图像处理技术将填料断面影像二值化,并提取石块边界; 图4 直剪试验PFC模拟Fig.4 Numerical modelling of the directshear test using PFC2D (2)通过Matlab编程提取二值图像中石块部分的像元坐标,并将其转换为PFC模型中的ball单元坐标,进而建立各石块的几何模型,完成块石建模;(3)在模型剩余区域填充土体胶结料的ball单元,完成土石混合填料的几何模型建模。三类典型试样二值图像及颗粒流数值模型见表1。借助断面影像二值化处理方法对试件中块石几何特征进行统计如表1所示,三类典型样的块石几何特征差异明显,其中A类样块石含量明显高于B和C类样;各试样的石块方向角各不相同,其中B、C样较为接近,其石块长轴方向近水平(与直剪方向近平行)。 表1 试样模型及含石特征统计 3.2.3颗粒接触模型及细观参数校核 根据岩土类材料的摩擦及粘结特性,土体胶结料和石块均选用接触粘结模型进行模拟。由于填方体粒径差异巨大,属高度离散介质,土颗粒与碎块石间的接触特性是影响土石混合体性质的重要因素,因此选用接触粘结模型,能够更好地反映土石混合体的力学行为[14]。 图5 胶结材料及砂岩块石直剪试验与数值模拟结果对比Fig.5 Comparison between laboratory experiments andnumerical simulations under different normal stresses 对于土体胶结物,采用直剪试验进行参数标定,数值模型尺寸为300 mm×400 mm(宽×高,与室内试验尺寸一致),包含3 569个颗粒,试验及模拟曲线如图5a所示。对于大粒径块石,由于其力学性质好于土体,通过单轴压缩试验(砂岩试样数值模型宽50 mm、高100 mm)来确定其细观参数,结果曲线如图5b所示。标定后的颗粒细观参数见表2。 表2 颗粒及颗粒间粘结参数 图6给出了剪应力-剪位移以及法向位移-剪位移模拟曲线。 图6 不同法向应力下碎块石土数值直剪试验曲线Fig.6 Numerical direct shear experimental curves ofgravel-block soil under different normal stresses 分析剪应力-剪切位移曲线可看出,碎块石土剪切过程中峰值及峰后剪应力-剪切位移曲线均存在较强的波动性;峰后出现明显的剪应力跌落,且法向应力越大跌落值越大,本研究中法向应力大于400 kPa时均存在较明显的峰后应力跌落;缺失大块石的C类试件(图6c)峰后出现渐进性应变软化特性,峰后应力下降随剪切位移逐渐减小,而且相对A,B两类试件其峰值剪应力相对较小(表明级配不匀劣化了土石混合物的剪切强度)。 另外,法向应力越小,相同剪切位移条件下产生的法向位移越大。法向位移从大到小依次为试件A、试件B和试件C,表明含石量越多法向位移越大,剪胀现象越明显。当剪切面附近含石量较小且级配不均匀时,峰后剪切位移达到一定值后,法向位移不再明显增加,如图6c中的试件C。 通过颗粒间力链与粘结破坏的演化过程来研究土石混合体填料的剪切破坏演化机制。由于依托工程填方工程普遍较高,故以法向应力为800 kPa为例,提取各试样在切向位移0.01,0.05和0.12 m时的颗粒间力链演化图(图7左,黑色表示相邻颗粒接触力链)和粘结破坏演化图(图7右,紫蓝色表示切向粘结破坏(剪破坏),红色表示法向粘结破坏(拉破坏))。 图7 填料试样A力链演化图与粘结演化图Fig.7 Force chain evolution of gravel-block soil 由图7可见,剪切起始阶段(切向位移0.01 m),填料模型的剪应力在胶结料和块石两部分中均匀分布,随着切向位移的增加(0.05 m),胶结料颗粒粘结逐渐破坏,试样中部粘结破坏以剪切破坏为主,上剪切盒左侧和下剪切盒右侧粘结以拉伸破坏为主。三类试样中,A类试样粘结破坏范围更大,A类试样中块石粒径最大且位置居中,大块石受力发生转动对周围颗粒粘结破坏有促进作用。力链演化图表明,胶结料承担的抗剪力逐步由块石来承担,试样中部形成贯穿大块石的明显力链,力链分布与块石位置有关。当切向位移继续增大(0.12 m),块石和胶结料接触力均变小。此外,图7还显示出,切向位移增大到0.05 m之后,试样剪切面两端和中部块石周围出现明显白色(表示相邻接触的颗粒已经相互脱离)脱空区域(红色框内),表明此处颗粒发生滑移,颗粒之间的孔隙增大;增大至0.12 m后,破坏绕大块石进一步扩大, 孔隙等值线图(图8)中部逐渐形成有明显分叉、绕块石特点的剪切带。 图8 填料试样A孔隙演化图Fig.8 Porosity evolution of gravel-block soil 试样B的力链演化与粘结破坏具有与试样A类似的规律,但由于试样B中块石直径较小,粘结破坏以及力链集中的范围均小于试样A。对于试样C,由于其剪切面附近无大块石,粘结破坏向剪切面上、下两侧发展程度较小。 由三类碎块石土试样(A类、B类、C类)数值模拟直剪试验得到不同法向应力下的峰值剪应力,根据摩尔库仑强度准则,得到夯后碎块石土的剪切强度参数(图9)。图9表明A,B,C三类试样的黏聚力和内摩擦角依次减小。因此,就本文所研究的碎块石土来说,含石量越高其抗剪强度越高,且当级配不匀(中等粒径石块缺失)时剪切强度将减小。而另一方面,含石量较高特别是级配不匀时,在降雨及地表水(如库水、河流)作用下,渗透系数相对更高,易出现潜蚀及浸蚀破坏,进而使得土石混合堆积体结构破坏及强度参数降低,造成边坡及地基的损伤、破坏[15],造成较多降雨诱发堆积体滑坡及库区等涉水堆积体的滑坡灾害[16]。 图9 碎块石土剪切强度-法向应力关系曲线Fig.9 Curves of shear strength and normalstress of grael-block soil (1)建立一种基于图像处理技术与筛分相结合的碎块石土真实结构及级配信息提取方法。石块部分通过图像处理技术提取粒径参数,而土体部分通过筛分获得级配参数。 (2)根据碎块石土结构及级配信息,采用离散元方法,提出了将碎块石土中的土体及块石力学性质分开标定的数值仿真思路。 (3)江北机场夯后填料在剪应力临近及达到峰值后,其剪应力与法向位移具有波动、跳跃特征,且剪切面附近块石粒径越大,数量越多,曲线波动越明显。随剪切位移的增加,剪切面附近孔隙度逐渐增大,试样中部逐渐形成近水平带状剪切带,且具有分叉、绕块石扩展特征。 (4)颗粒粘结破坏具有局部化特征,初期抗剪力由胶结料和块石共同承担,之后胶结料承担的抗剪力逐步向块石转移。临近峰值及峰后,抗剪力主要由块石承担,力链分布极不均匀。 (5)针对本次研究,碎块石土中含石量越多,黏聚力和内摩擦角越大,级配不匀会造成剪切强度的降低。剪切带附近含石量越多,剪切带宽度将增大。3 夯后填料直剪数值模型的建立
3.1 模拟对象及石块-土体分界粒径
3.2 数值模型的建立
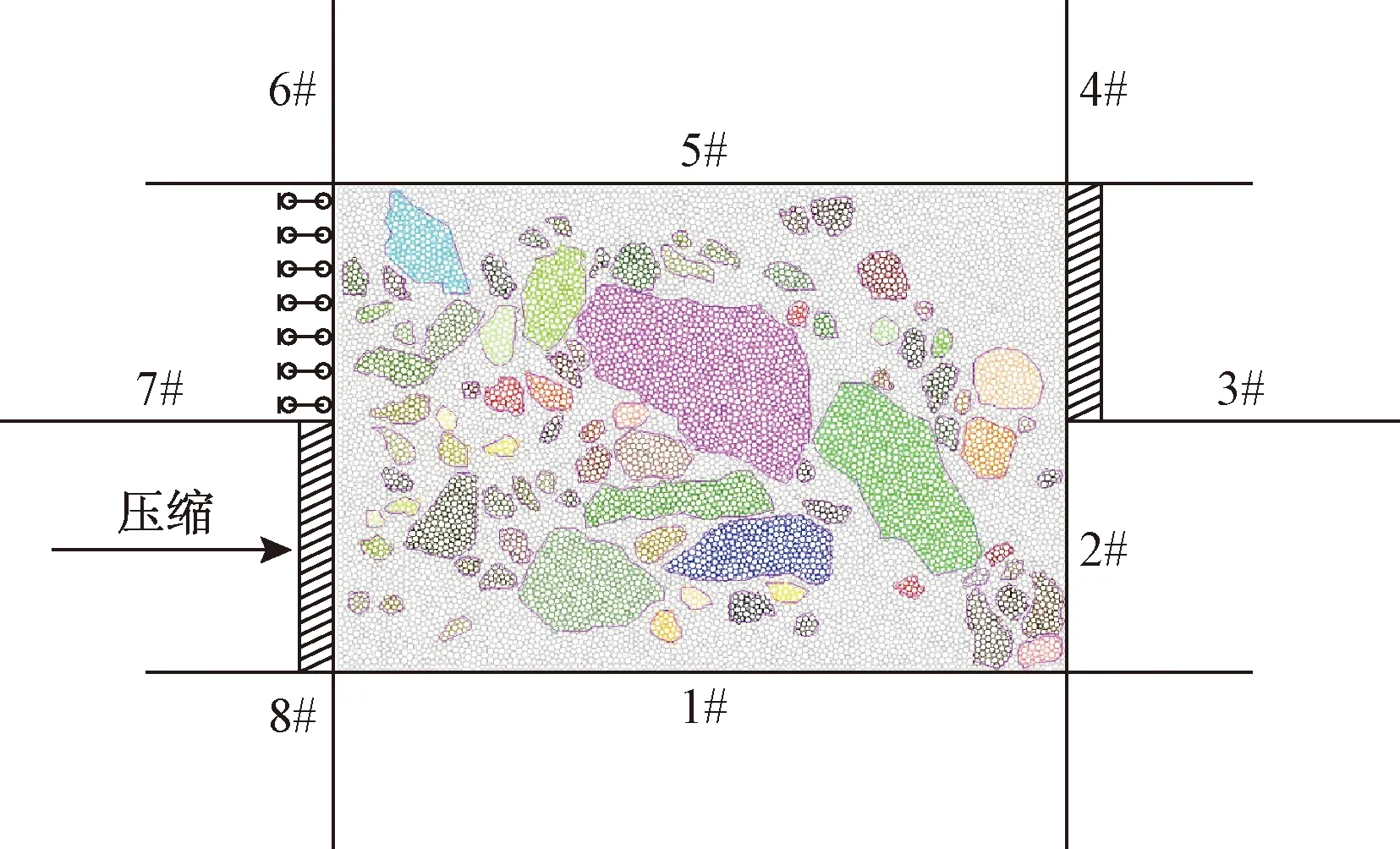



4 模拟结果分析
4.1 法向位移-剪位移曲线

4.2 破坏演化

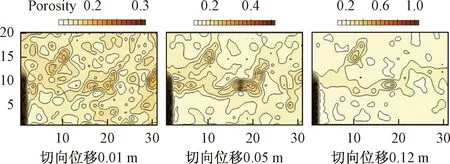
4.3 剪切强度

5 结论

