融入数学体验活动的教学实践与思考——以“作一个角等于已知角”为例

张爱平 沈雪英

(江苏省南京市金陵汇文学校 210036)

数学体验活动是学习者置身某种场域中，参与的特定的数学活动，是学习者亲历具体的操作过程，感受数学对象，发现数学问题，领悟数学思想方法，积累数学活动经验，提升数学关键能力的一种学习方式，包括由环境刺激产生的情感体验活动、实物操作产生的行为体验活动和内省反思产生的认知体验活动，不仅有外部操作中的发现、验证和探索，还有注重内隐感知、领悟和自我建构．通过数学体验活动，学生积极参与，主动思考，理解数学本质，经历数学方法的形成过程，积累数学活动经验，发展数学能力．本文以“作一个角等于已知角”为例，谈谈融入数学体验活动的课堂教学实践及思考．

1 教学背景

尺规作图的提出可追朔到古希腊时期，它是指用没有刻度的直尺和圆规解决一些平面几何作图问题．直尺的功能就是画直线，圆规用来画弧线或者截取相等长度的线段．尺规作图剔除了线段的刻度和角的角度，将刻画基本图形(线段、角)大小的“数”问题转变为“形”的问题，可以培养学生的数学操作能力和逻辑思维能力.

1.1 课标及教材内容要求

《义务教育数学课程标准(2011版)》(以下简称《课标》)相对《全日制义务教育数学课程标准(实验稿)》对尺规作图的教学提出了更高要求，在“学生要保留作图痕迹，知道作图步骤“的基础上提出”要能了解每一步步骤的道理”的要求，即既要会“作图”， 辨清步骤，又要能 “明理”，弄清原理．

(1)能用尺规完成以下基本作图：作一个角等于已知角；

(2)在尺规作图中，了解作图的道理，保留作图的痕迹，不要求写出作法．

《课标》对学生的学习提出高标准，教师的教学行为必然也要相应的改变．

“作一个角等于已知角”是苏科版七年级上册第6章平面图形的认识(一)6.2节中的一段教学内容．教材中是这样叙述的“议一议 只用直尺和圆规，怎样作一个角等于已知角？”“做一做 阅读下列作法，并根据作法中的步骤用直尺和圆规作角．”

1.2 教学现状及学情分析

“作一个角等于已知角”是五个基本尺规作图之一，在多年的教学中，常常遇到这样的尴尬情形，学生刚学习这个作图时掌握的很好，过一段时间后就几乎全部遗忘．反思以往的教学，也许是过多地注重作图步骤和技巧，而忽视呈现作图步骤是如何自然产生的，学生“依葫芦画瓢”，缺少对作图步骤生成的体验，缺少对已有画图经验的联系，这就导致学生对这个作图的掌握停留在机械操作层面，知其然，而不知其所以然．

学生已有的知识和经验有：作一条线段等于已知线段，知道角是由公共端点的两条射线组成的图形，用量角器画一个角等于已知角．学生已了解直尺和圆规的功能，知道作一个角的关键是终边的确定，这些都为本作图的体验教学提供了保障．而尺规作图一般步骤是：想象图形，画出草图；分析草图，形成作法；尺规操作，规范作图；证明等．但是此作图的理论证明要在八年级第一章全等图形学习后才能完成，利用“边边边”证明三角形全等，再根据全等三角形对应角相等，这阻碍了本节课作图操作后逻辑推理论证的完成．《课标》提出了“会作” 与“明理”的双重要求，受教材体系和学生已学知识的限制，“证明”是无法在本节课中实现，那么能不能让学生先在体验活动中“明理”呢？七年级学生的思维正由直观形象思维向抽象逻辑思维的转变，学生的分析能力和逻辑推理能力有待提高，这就要求教师准确把握教学的方向，设计符合学生的认知最近发展区的体验活动，将探索作法扎根在体验中，学生在自我的探索中获得准确的作图步骤，“明理”前置，以“理”生“法”，学生自主“生成”作法.

2 教学设计

尺规作图体验活动的设计要充分体现直尺和圆规的强大功能，于无形中化“无刻度”为“有刻度”，引导学生自主探索作法，完成知识的承接，实现认知的自然过渡．作一个角等于已知角的关键是确定角的终边，而确定终边的关键是确定这条边上的另一个点，所以这个尺规作图的难点就是如何确定终边上的这个点，将确定边的问题转化为确定点的问题．终边上这个点的确定，又与已知角的终边上的哪个点对应，这个“标志点”该如何确定，这个“标志点”的确定对要作出的角终边上的“对应点”的确定有怎样的帮助呢？笔者根据体验学习的内涵，设计的三种体验活动，旨在引导学生自然生成作图方法，发展学生学习、探索新知的能力．

2.1 在同一个圆里找两个相同的扇形

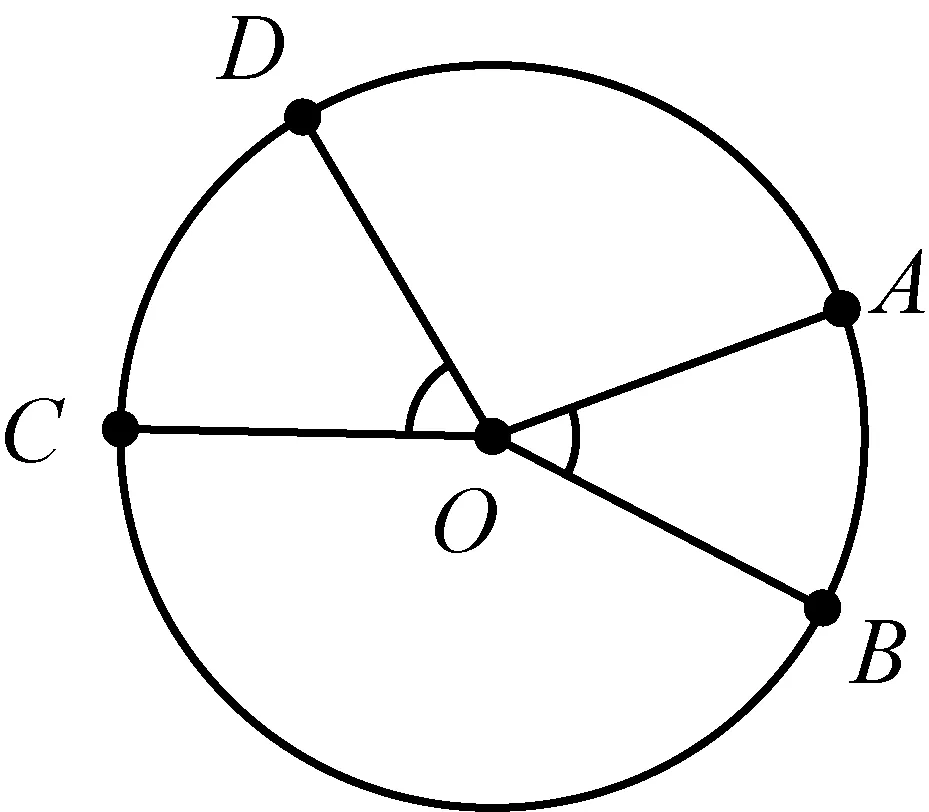
图1

如图1，已知∠AOB，在这个圆中找一个∠COD，使得∠COD=∠AOB．

借助这个已知圆，根据“同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．”要找到相等的圆心角，只要用圆规量出长度相等的弦长．

体验过程的反思：圆的出现过于突兀，圆的性质是九年级的内容，学生的知识储备还不够．

2.2 做两把相同大小的折扇

如图2，要制作和它一样大小的一把折扇，我们要准备什么尺寸的材料呢？

学生容易想到选同样大小的弧形纸作扇面和同样长短的竹片作扇柄．扇柄的长度是圆弧半径的大小，纸面的大小可以决定纸扇张开的角度大小．一般折扇制作的三步骤，固定一根扇柄—糊纸面—固定另一根扇柄，这个过程和“用尺规作一个角等于已知角”的过程非常的类似．

图2

体验过程的反思：(1)制作纸扇准备的材料繁琐；(2)制作纸扇耗费时间，数学课堂成了手工课堂；(3)扇面纸的大小的裁剪学生更容易想到用叠合法去裁剪，那么扇子的张角的大小的确定更容易联想到扇面纸面积的大小，不容易转化到弧长的大小，因此作一个角等于已知角的第二条线上的这个点不容易自然生成．

2.3 量角器画角的演变

问题1回忆小学时是怎样用量角器画一个角等于已知角的？量角器的功能是什么？

如图3，量角器画角的一般步骤，先量出已知角的度数，再根据度数画出另一个相等的角．在“量”这一阶段可分为三步：对准顶点、重合始边、读出终边所读的数值；“画”这一阶段也可分为三步：画始边、根据数值点出终边上的一个点、画终边．此时，量角器的功能是确定角的度数．

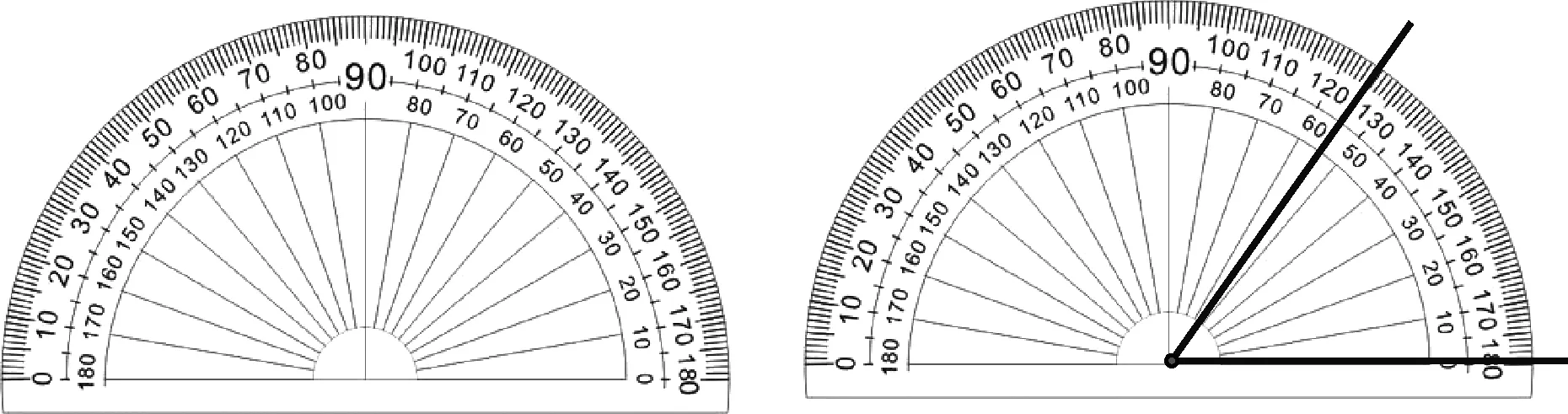
图3

问题2如果量角器的刻度看不清楚了，你还能用它画出这个角吗？此时量角器的功能又是什么？

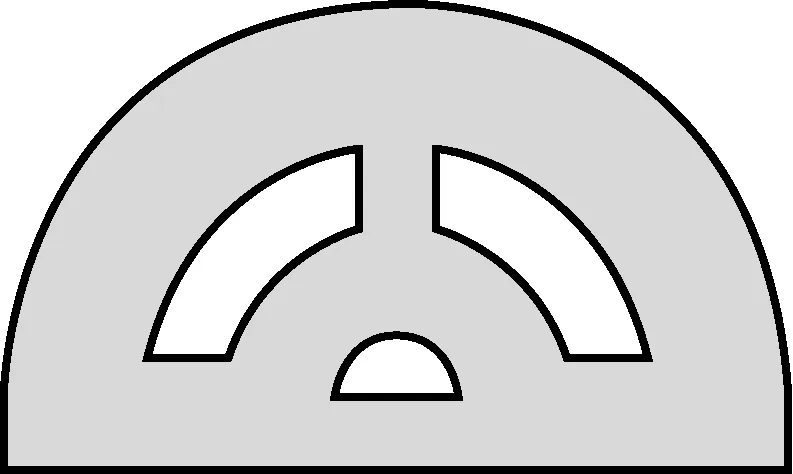
图4

图5

如图4，量角器没有刻度了，那么在“量”这一阶段中的前两步：对准顶点、重合始边仍可以完成，第三步读出终边所读的数值无法进行了．结合“画”这一阶段的画好始边后点出终边上的一个点遇到了障碍．那没有数值了，该怎么确定终点上的这个点？

如图5，学生就会发现，在量角器上相应的位置上作个“标记点”即可完成上述的操作．此时量角器的功能就弱化为找圆弧上的一个“标记点”了．

问题3如果没有量角器，只有类似量角器的外轮廓的半圆弧，你能借助圆规和直尺画一个角等于已知角吗？

完成问题2时，学生已认识到量角器的功能从“数”转变为“形”了，没有了刚才无刻度的量角器这一工具，半圆弧上如何去替代刚才“标志点”？

如图6，利用圆规创造量角器的弧，这时候，另一个和已经存在的等半径的半圆就自然会被画出来．如何度量弧线的长短呢，圆规能确定线段的长短，要确定弧线的长短，只有“化曲为直”，通过确定以弧线两端点为端点的线段的长短去确定弧线的长短，这样确定“标志点”的另一条弧线也自然生成．

图6

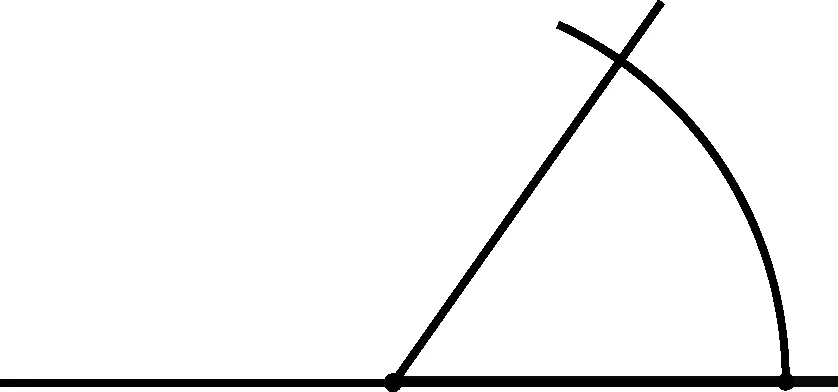
图7

问题4如图7，擦去半圆中多余的弧线，只留下确定终边上点的位置的一小段，请根据刚才的操作探索过程，用圆规和直尺作一个角等于已知角．

学生回忆活动的全过程，经历了“量角器-没有刻度的量角器—半圆—圆弧”的画一个角等于已知角的过程，用“尺规”作一个角等于已知角的步骤已了然，如图8，具体作法如下：

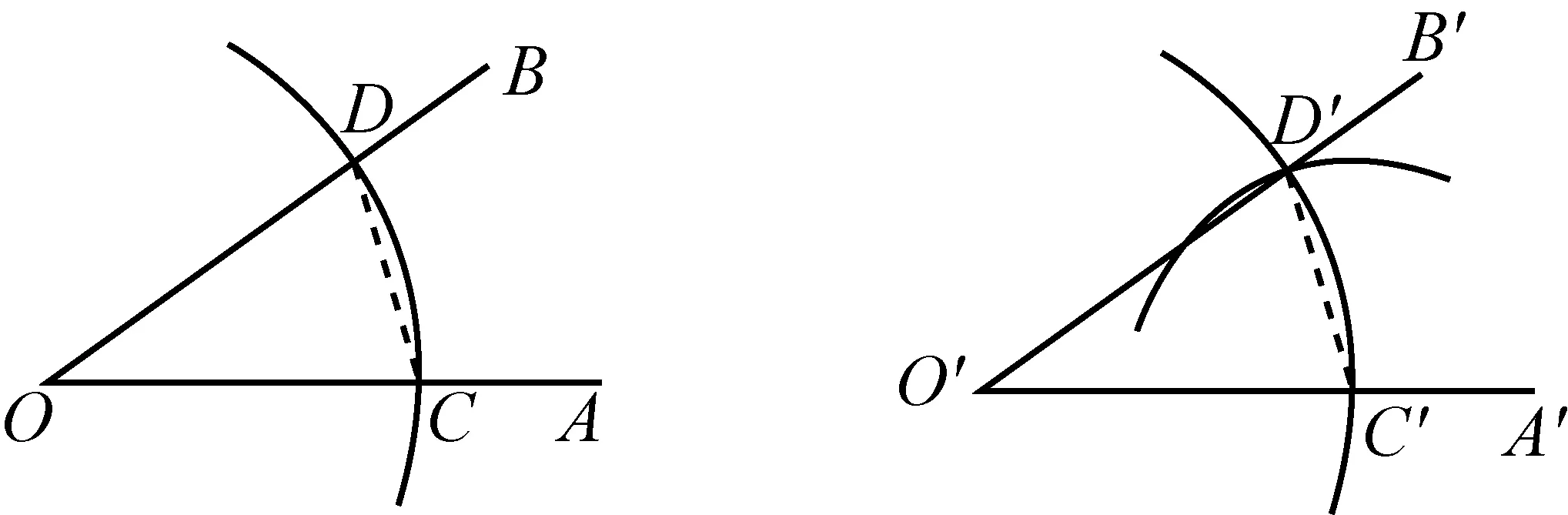
图8

(1)以点O为圆心，任意长为半径用圆规画弧，分别交OA、OB于点C、D.

(2)任意画一点O′，画射线O′A′，以点O′为圆心，OC的长为半径画弧交O′A′ 于点C′.

(3)以点C′为圆心，CD长为半径画弧，交前弧于D′点.

(4)过D′画射线O′B′，∠A′O′B′就与∠AOB相等.

3 教学思考

正如苏霍姆林斯基所说：“对于儿童来讲，掌握知识这个最终目的不可能像成人那样成为他付出智力努力的主要动力．学习愿望的源泉在于儿童智力劳动的性质，在于思想的情感色彩，在于理性的体验．如果这个源泉涸竭了，任你用什么办法也不可能让孩子坐下来念书．”这里设计合理的体验活动，改变了以往教学时作法的复制和灌输，根据学生已有的知识和经验，引导学生参与数学思维探究活动，在体验活动中自然形成数学方法、充分理解数学本质．学生的学习过程是一个自己理解、自主建构新知的过程，学生带着自己原有的知识、方法、经验去主动体验、思考、反思，建构新的知识体系，提升数学操作能力和逻辑思维能力，积累新的数学活动经验，提升学生的学习力.

3.1 数学体验活动要合理充分

首先，选取体验材料要合理．本文的三种设计分别选取了圆、折扇、量角器三种素材，它们或多或少都与“作一个角等于已知角”作法的探索有着内在的联系．但是综合考虑学生对素材的熟悉程度、对已有经验的联结紧密度、对对象的本质特征相似度等因素，量角器无疑是最合适的材料．由此可见，选取最合理有效的操作工具，便于学生按照自己探索的操作步骤动手画图，自主形成作法．合理的体验材料便于学生进行数学活动，自然地引发数学思考，在不同材料的体验使用中科学选择.

其次，学生体验的过程要充分．库伯教授构建的体验学习模型“体验学习圈”：具体体验—观察与反思—抽象概念—在新情境中体验，依次循环．在选择量角器作为体验材料后，笔者设计的体验活动分为4个层次，量角器画角—无刻度的量角器画角—半圆弧画角—尺规作角，每个层次的活动都经历了具体体验、观察反思形成经验、再弱化工具、再次体验形成新的经验，循环了3次后，学生的体验过程充分．尺规作图贵在思路的形成，将一个角搬到另一个位置，用圆规和直尺精确地作出来，这样的自主探究、找寻原理、发现作法可以确保学生知识形成的基础牢固，相应的作法生成自然无痕，学生经历了“角的尺规画法”的形成过程，通过探究式的体验活动，理解数学本质，符合学生的认知规律.

3.2 数学体验活动要融合迁移

迁移是指学习者把理解的知识、形成的基本技能迁移到不同的情境中去，促进新知识、方法的学习或解决不同情境中问题.“利用尺规画一个角等于已知角”的探究过程中，融入必要的体验活动，适时调用小学时量角器画角的活动经验，分析得出尺规作角与用量角器作角之间的共性，将量角器画角中的基本方法和经验，类比迁移到利用直尺和圆规画角的过程中，教师准确激活学生原有的知识、方法和经验，设计体验活动，引导学生从简单熟悉的问题开始，不断变更背景，寻找素材的内在联系，完成知识、方法的自主建构．体验活动过程的条理化，活动经验的领悟，实现数学思想方法的融合和发展，这样的体验学习过程贴近学生认知水平，符合最近发展区理论，搭建起新旧知识之间的支架，引领学生学会思考，掌握分析方法，明确作图步骤，利用不同工具的画法迁移合理自然.

3.3 数学体验活动要发展能力

《教育部关于全面深化课程改革 落实立德树人根本任务的建议》指出核心素养是学生应具备的适应终身发展和社会发展需要的必备品格和关键能力，在数学课堂教学中融入体验活动，就是要帮助学生培养和发展数学学科的关键能力. 尺规作图是一种情境的创设，由学生自己动手作出一张符合要求的图形，这是几何教学中难得的实践活动，是让学生从操作体验提升到理论认识的重要途径．尺规作图的完成是学生动手操作和几何推理相结合的结果，其几何直观能力、几何推理能力、空间想象能力等数学学科关键能力得到发展；作图前的体验活动，学生动手度量、拼凑、截取、叠合等几何操作过程，具有不可替代的直观性，为其数学学科关键能力的发展添砖加瓦．

尺规作图是人类理性思维的瑰宝，它的教学方法没有固定的模式，但是“明理” 才能 “得法”．在数学体验活动中，留给学生更多自主探究、思考分析的空间，多动手，多探究作图的原理和作图方法，融入了体验活动的学习，发展了数学学科的关键能力.