基于线性规划单纯形法优化矿岩调运研究

王晓冬

（长春黄金设计院有限公司，吉林 长春 130000）

矿岩调运是组成矿山系统项目的的重要环节，能按照露天矿经营规模，给采矿及剥岩科学配置运输计划，设计经济最佳的流向，令总运输费用最少。露天矿原矿和岩石运输量较大，运输费占采矿年运营费的30-50%，减少运费是降低采矿生产投资的有效渠道。通过合理的方法求出最好调运方案，能够尽量节约运输成本。国内大多数露天矿岩调运通常是靠经验进行，对矿岩的运输总量及去向配置极少有统一计划，随机性及盲目性较大，造成在生产阶段岩石无法根据最佳线路排至相关排土场，岩石运送功无端加大，导致排岩费用增多，严重影响到企业经济利润。完善矿岩调运计划，使矿山生产运输设施发挥最大的作用，对矿山单位提高经济收益作用较大。

1 线性设计单纯形法的数学模型

单纯形法是处理线性规划工作的重要算法，它的求解基本思路见图1所示。针对一个可行不空并有最佳解的线性规划现象，经在可行区的边缘上寻求与变换基础可行解而最后求出最佳解。

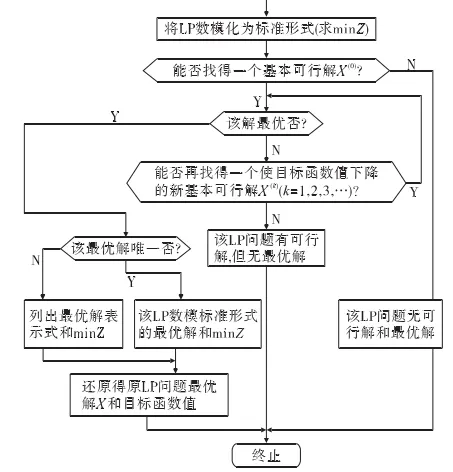
图1 单纯形法求解的具体思路

采取线性设计单纯形法求出运输问题时，要先将运输问题转变为规范矩阵模式的数学模型，建立（m+1）·（n+1）矩阵初期单纯形表。若规范化后的目标函数式子右边包含常数项，于列表时将之从计算早期就参加矩阵调换。根据规范化后数学模型上的各信息所出现的初期单纯形表，根据表中参数矩阵上是否存在一个m阶单位系矩阵，然后分两个环节进行计算。鉴别与寻求新的基础可行解为单纯形法的重点。当鉴别求出的基础可行解是非最佳解后，就应在该基础上继续寻找令目标函数值降低的新的基础可行解，经矩阵的旋转调换，令系矩阵上存在一个m阶家单位系矩阵I0，然后使新单纯形表上的I0为基，就获取一个新基础可行解，判定是否非唯一最佳解后接着求其所有最佳解。若已获得一个不符合最佳性鉴别规定的基础可行解，而又不能再获得一个目标函数值降低的新基础可行解，就判断该问题存在可行解但无最佳解。

2 矿岩调运计划及各项参数设置

2.1 矿岩运输问题处理计划

单纯形法所具备的数学参数为剥岩量、运送量及单位运输费用，先求得各项参数和给出各项参数的计算方程，然后制定运输算平衡表及运价表，确定生产能力、剥岩量、运送量及单位费用，将具体生产产问题变成数学模型，按照设定的约束条件，创建线性设计单纯形法约束式子，根据计算法流程制定计算流程，获得方程最佳解，就能得出运费最低的矿岩调运计划。

矿岩运输所需处理的问题是以最少的运输费用将开采矿石和剥离矿石运输到指定地点。矿山各采区开采能力不变，矿石岩石产量不变，各排土场的容量不变，并且一定要将所有剥离岩石运送至相关排土场，从每个采区至各排土场的运费及运量是线性关系[1]。假如矿山采场包含m个采矿及剥离工作面，把岩石运送n个排土场，剥岩量和排弃量相同，是运筹学方面的平衡运输内容。根据图1求解思路将所计算的平衡运输内容转变成线性设计单纯形法数学模型，求得最佳解，找出令总运费最低并符合剥离岩石和排弃岩石相同的最佳运输计划。

例如：采矿开采能力i运向排土场j的基本运价是Cij=1、2···，m；j=1、2···，n，Xij达标开采能力i到排土场j的最好运量，Z是最低总运费，就采取线性设计原理建立数学模型。其中。目标函数为：

制约条件1：

制约条件2：

非负条件： 0≤Xij （4）

2.2 各项参数的设置

线性设计单纯形法求解的重要步骤是按照采场开拓运送模式及运输排土形式，制定平衡表与运价表，各项计算参数的运算是求解的重点，各参数要按照其影响要素逐一求出。

（1）采场车辆运距的设置

采场车辆运距包括固定线与移动线两个方面，其表现模式均是具体信息矩阵。固定线运距可以图上量取也可现场测量；移动线运距就和多种因素相关，如采矿方式为横向推进或者纵向推进、采取哪种运输模式、各开采期间的采购量等，要按照每年及上年度的采场规划年终图展开计算与检测[2]。采场移动线运送距离的设置比较复杂繁重，信息量较大，对计算环节及最后结果影响很大。

（2）车辆效率回归式子

按照运距以及现场运输设施型号、尺寸、设备性能、公路坡度、路况和现场具体统计的样品信息，求得车辆运送效率和运距的回归式子。采取EXCEL的回归研究作用，将收集到的车辆形成月报表相较于运距的现场样品数值录进EXCEL表格，制定散点图，按照信息和散点图做回归分析，获得车辆效率和运距的回归式子曲线，如图2所示。

图2 车辆运距与运送效率回归式子

（3）车辆运费回归式子

车辆运费指标要按照运距，以及现场运输设施型号、尺寸、设施性能、耗油系数、轮胎耗损、运送路况、目前所用燃料价格与人工成本等因素，按照现场具体统计的样品信息，求得车辆运费和运送距离的回归式子，按照信息和散点图做回归分析，获得车辆运费和运距的回归式子，如图3所示[3]。

图3 车辆运距与运费回归式子曲线

例如：85吨矿用电动轮自卸车辆的运费回归式子：

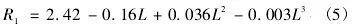
其中，L代表车辆运距，千米；R1表示车辆运输成本，元/（t·km）。

（4）铁路运输成本回归式子

同理，根据场地铁路机车与汽车设施型号尺寸、质量、线路坡度等多种因素，以及现场详细统计的样品信息，求得铁路运费和运距的回归式子以及曲线图。回归方程是：

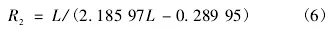
其中，L表示铁路运距，千米；R2表示铁路运输成本，元/（t·km）。

（5）胶带机运输成本回归式子

根据场地胶带机设施型号、尺寸、性能、耗电系数、材料耗损、胶带机坡度等多种要素，以及现场具体统计的样品信息，求得胶带机运输成本和运距的回归式子与曲线图。

回归式子：

其中，L表示胶带机运距，千米；R3表示胶带机运送成本，元/（t·km）。

运距表制定的重要依据为计算运距与各运输模式的运输运营成本，单位运营成本Cij要按照所采取的设施状况及运营成本指标，分别求出车辆、铁路及胶带机运营成本指标，要考量资金时间价值的作用[4]。根据上述方式求出的Cij是静态值，未考量成本的时间价值，要及时调整。而各种成本要根据动态计算，即求出每一项成本时，考量到该项成本的支出时间，把该年的成本开支贴现至计量基准年，即：

其中，NPV表示净现值；D代表矿山总期限；Fy表示第r年的资金流量；Mr表示一次偿还复利指数；1/Mr表示一次偿还限值指数；P8表示投入基准效益率；Er表示采矿年份。

根据一般的设计流程在矿石运输设计中，通常不得给出开采进程方案，只能明确矿石产量和各性能的分层岩石量，因此，要精准计量Er是很困难的，仅能按照现有的分层岩石量大概计算每种能力的采矿年份Er。即：

其中，Er、Er-1分别是r水平与r-1水平的采矿年份；Xr表示r性能的分层岩石量；万吨；P3表示岩石年产量，万吨/a。

调整后的运价是：Cij=Cij/Mr（元/吨）。

3 结论

第一，矿山运输过程存在很多可行的运输计划，采取线性规划单程形式理论创建数学模型，制定运算流程求解，是完善矿岩调运的有效举措。利用单纯形法运算流程找出矿岩运输最佳方案，尽量节省运输成本。第二，运算流程求解迅速，精度大，省时省力，还能够按照现场具体参数的改变立即调整，可以有效应对矿山具体生产环境的改变。第三，线性规划单纯形法还可以为生产管理人员决策进行服务，在处理包括多项约束变量情况时给出最佳决策。在指定资源环境下怎样发挥最大经济价值的问题，也能采取该方法解决。