基于少量导联的脑-机接口实现方法研究

施晨韵，吴小培，殷 婵，欧阳蕊

(安徽大学 计算机科学与技术学院，合肥 安徽 230601)

脑-机接口(brain-computer interface， BCI)是人-机交互技术的一种特殊实现模式。BCI系统通过对任务相关神经活动进行信号处理、特征提取和分类，实现思维活动和控制命令的转换，进而实现大脑对外部设备的直接控制[1]。

头皮脑电(electroencephalogram，EEG)是一种常用的神经活动获取方法。基于EEG的BCI(EEG-BCI)实现方法具有无创、高时间分辨率、操作简单和成本低等明显优势，近年来一直是BCI领域的研究热点[1-2]。但是EEG信号容易受到眼电、肌电和心电等生理伪迹以及外部电磁环境的干扰。此外，受大脑容积传导效应的影响，EEG的空间分辨率通常较低。因此EEG-BCI系统的实现对EEG信号处理和模式识别方法提出了很高的要求。

研究表明，基于多导联EEG的空域滤波技术能有效改善BCI系统性能[3]。Ramoser等首先提出采用共同空间模式(common spatial pattern， CSP)对运动想象脑电进行空域滤波和特征提取[2]，获得了非常理想的分类效果。目前，CSP空域滤波方法被广泛应用于BCI研究领域。CSP是一种有监督设计方法，其性能与训练样本规模、质量以及EEG导联数量等因素密切相关。为了获得有效数量的训练样本，通常需要进行较长时间的数据采集工作。在此期间，受试者往往会因为疲劳和精力分散等原因影响数据采集质量，进而导致CSP滤波器以及BCI系统的稳定性不理想。独立分量分析(independent component analysis， ICA)是一种多通道盲源分离方法，其特点是能实现有用信号和干扰噪声的有效分离[4]。相比CSP的有监督设计，ICA属于无监督设计方法，因此训练样本采集相对比较容易。Kachenoura等充分肯定了ICA在BCI系统实现中的应用价值和潜力[4]。但到目前为止，相关研究报道还比较有限。根据现有的文献资料[4-5]，ICA输出排序的不确定性以及对EEG导联分布的过于敏感可能是阻碍其实际应用的主要原因。

本文围绕运动想象脑-机接口的实现问题，对少量导联情况下的ICA-BCI系统设计和性能评估方法开展研究，提出采用自测试技术对ICA滤波器进行了优化设计。论文采用BCI competition IV-2b公开数据集对本文方法进行了测试[6]，实验结果验证了所提方法的有效性。

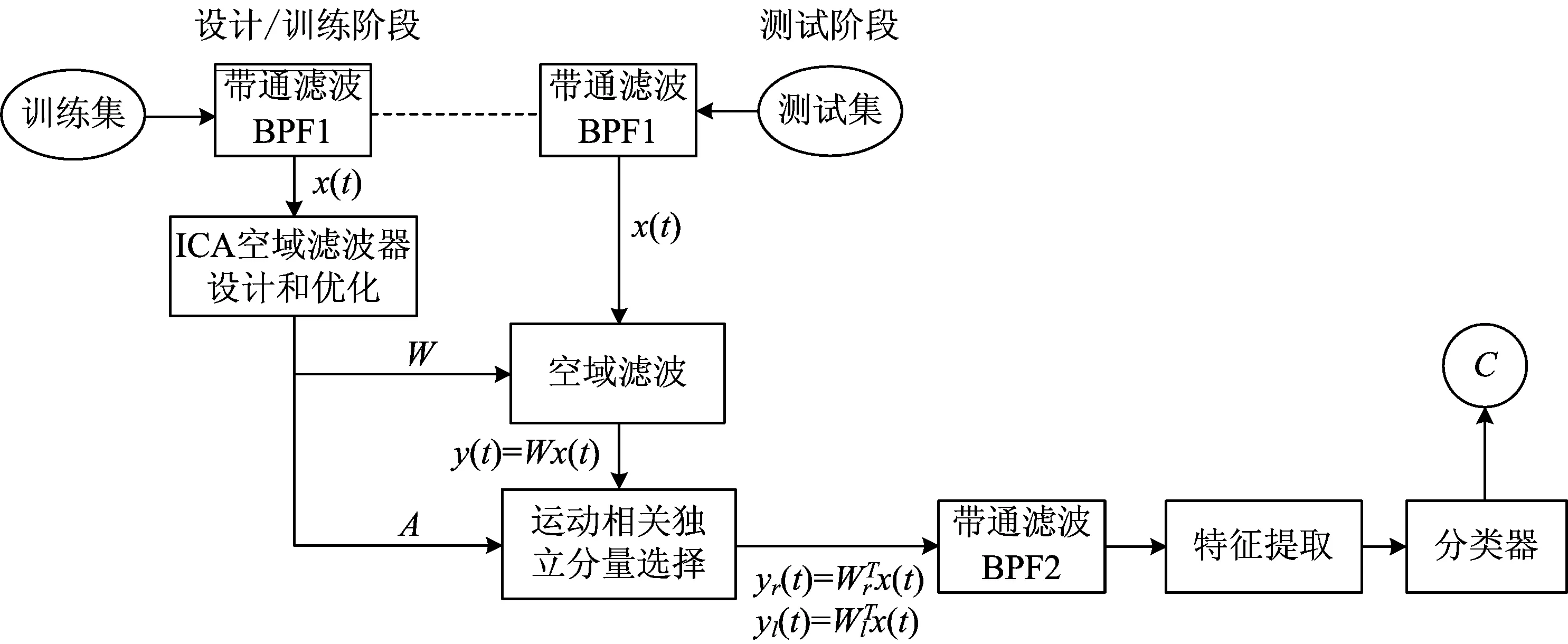
图1 MI-BCI系统实现框图

1 方法

神经电生理研究表明，当肢体进行真实运动或者想象肢体运动时，大脑运动皮层EEG中的mu/beta节律成分会出现幅度调制现象，称之为事件相关同步或去同步 (event-related synchronization/desynchroni- zation，ERS/ERD)[1-2]。通过对多通道EEG的分析和处理，可获取与运动想象(motor imagery，MI)类型相对应的EEG特征，在此基础上，通过对EEG特征进行分类，可实现从肢体运动想象到控制命令的转换。基于这一原理所建立的BCI系统称之为运动想象BCI系统(MI-BCI)。

图1给出了本文MI-BCI系统的实现算法框架，其中包含系统“设计/训练”和“测试”两大部分。具体包括常规的时域带通滤波器(BPF1，BPF2)的设计和ICA空域滤波器的设计及优化。然后将所建系统模块应用于测试集中单次试验的分类。

1.1 ICA空域滤波与运动相关独立分量选择

根据图1所示MI-BCI系统框架，采用ICA空域滤波器对带通滤波后的多道EEG信号进一步处理，以获取与左/右手运动相关的EEG源成分。ICA算法假设n个头皮电极记录的多道EEG信号x(t)=[x1(t),x2(t), … ,xn(t)]T是m个相互统计独立的隐含源信号s(t)=[s1(t),s2(t), … ,sm(t)]T的线性瞬时混合，即：

(1)

式(1)中，A为n×m常系数混合矩阵，不失一般性，通常假设n=m。在源的独立性假设前提下，ICA利用多道观测数据x(t)进行分离矩阵(W=A-1)估计和隐含源的提取，即：

(2)

式(2)中，y(t)=[y1(t),y2(t), … ,yn(t)]T是对真实源s(t)的逼近，分离矩阵W中的各行向量wi,i=1,…,n称之为ICA空域滤波器，用于提取不同的独立源yi(t)=wiTx(t)。

基于不同的源独立性度量方法，研究者提出了若干经典ICA算法，如Infomax算法、FastICA算法、Jade算法以及Sobi算法等[7-10]。本文采用基于超高斯模型的Infomax算法。分离矩阵W的迭代学习规则如下[7]：

(3)

式(3)中，E为统计平均运算，sign是符号函数，μ为学习率。

由于ICA输出存在排序不确定性，因此如何从n个输出独立分量{yi(t),i=1,…,n}中自动识别出运动相关独立分量(motor related independent components，MRICs)是当前在线ICA-BCI系统实现的难点[4，11-13]。到目前为止，MRICs的自动识别还没有统一方法。本文根据独立分量在头皮电极上的投影系数，即与yi(t)对应的混合矩阵A的列向量ai=[a1i,a2i,a3i]T系数进行MRICs识别，它们之间的关系可由(4)式表达，其中，ai也称之为独立分量yi(t)空域特征。

(4)

本文所用数据为C3，Cz，C4三导联左/右手MI-EEG，其中C3/C4导联电极最靠近左/右手运动皮层区域。根据神经电生理原理，MRICs在C3或C4头皮电极位置应具有最大投影系数[2]。根据(4)式，x1(t)，x2(t)，x3(t)分别为C3，Cz，C4电极的三路EEG信号。经ICA运算后，独立分量yi(t)在三个运动皮层头皮电极位置的投影系数为a1i、a2i、a3i，如果|a1i|(或|a3i|)为三个系数中的最大值，则判断yi(t)是左手(或者右手)MRIC。文中分别用yl(t)(或yr(t))表示，与之对应的分离矩阵行向量wl(或wr)为MRICs空域滤波器，它们之间的运算关系如(5)式。

(5)

1.2 ICA空域滤波器的设计和优化

ICA空域滤波器的设计不依赖训练数据的标签信息，是一种无监督设计方法[13]，这是ICA方法的优势。在已报道的研究中，为了充分利用训练样本中的统计信息，通常建议尽可能多的采用训练数据进行ICA滤波器设计，但这一传统思路的有效性和可靠性有时难以保证。原因是：1)实测EEG训练样本中的某些时段可能会包含比较严重的噪声干扰，如果不进行训练样本筛选，很难保证ICA空域滤波器的性能；2)过多的EEG训练样本会显著增加ICA运算的复杂度，降低BCI系统的实用价值[11-12]。

本文采用“自测试”技术对训练样本进行选择，进而实现对ICA空域滤波器的优化设计。具体实现过程如图2所示。自测试过程包括以下几个关键步骤：1)从训练集保存的连续EEG样本中，截取一段时长为T秒(经验值为100秒左右)的数据段用于ICA空域滤波器的设计[12]；2)基于所得MRICs滤波器[wl，wr]，对训练集中全部单次试验数据xi，i=1,…,I进行MIRCs特征提取和分类，并统计识别率；3)按设定的时间步长Ts移动数据窗，获取新的训练样本段，重复步骤1)和2)，遍历全部训练样本，保存全部空域滤波器及其对应识别率结果。

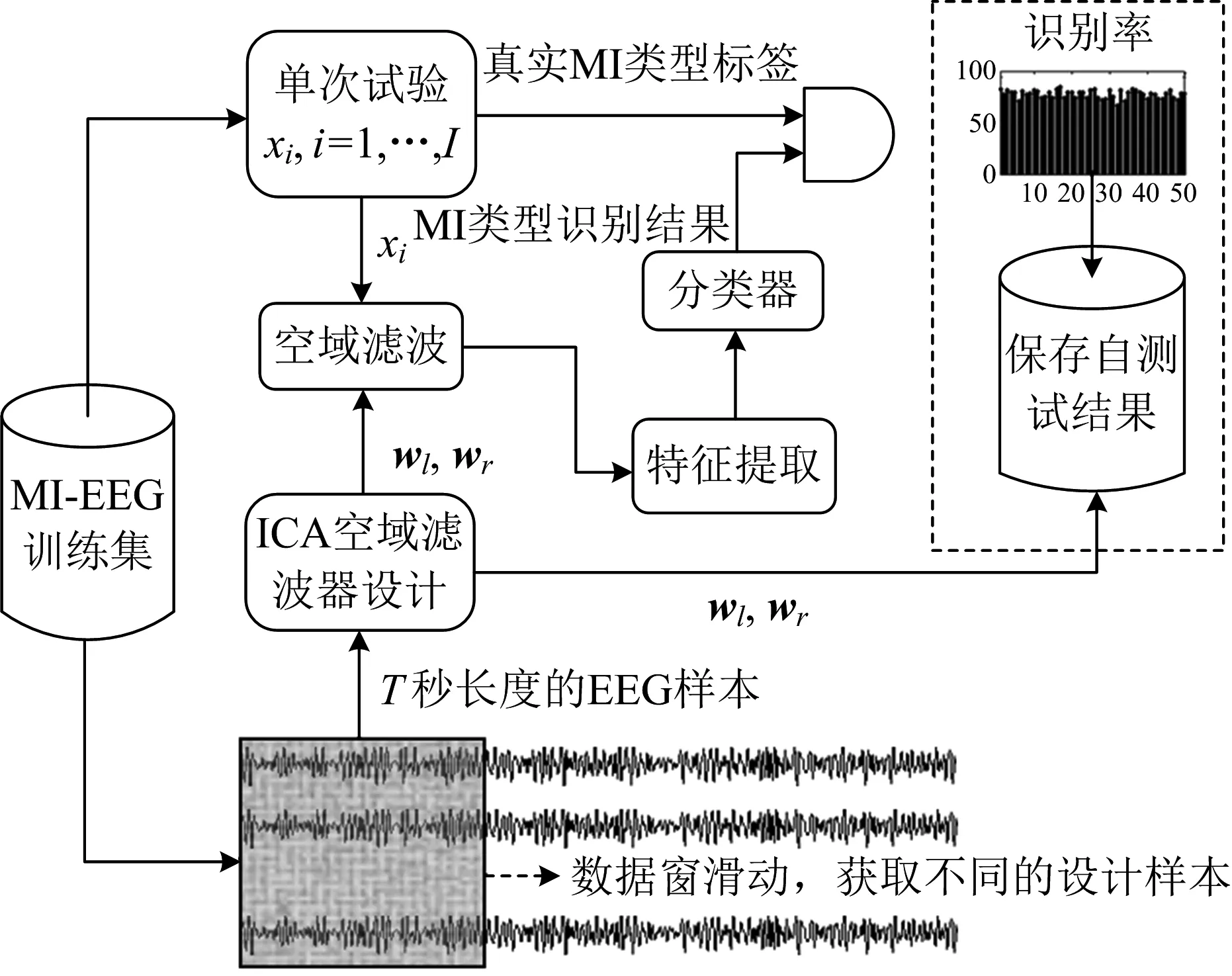
图2 自测试算法框图

1.3 时域带通滤波

在图1所示MI-BCI系统的设计和测试部分，采用了BPF1和BPF2两组带通滤波(均为64阶FIR线性相位滤波器)。对于全部9位受试者，BPF1采用统一频带范围：7～40 Hz。在BCI设计和测试阶段，BPF1用于对原始EEG数据进行带通滤波预处理，以增强运动相关的EEG成分并尽可能地抑制干扰伪迹。BPF2只用于测试阶段，其目的是对空域滤波器提取的运动相关EEG分量进一步增强处理。由于个体差异性，BPF2的频带参数需要根据不同受试者的MI-EEG特征进行专门设计。在本文的前期研究中，通过对9位被试训练数据(x_3T)进行时-频分析和“自测试”，获取了适合每位被试的BDF2频带范围，如表1所示。

表1 带通滤波器的频带范围

1.4 特征提取与分类

在获得左、右手MRICs并经BPF2带通滤波增强后，分别取yl(t)和yr(t)在运动想象时段的EEG样本(3.5～7.5 s，参见图3)，以该时段的信号能量El，Er作为特征：

根据运动想象诱发的ERD现象[1]，即被试在进行左/右手运动想象时，肢体对侧运动皮层的μ节律幅度会出现抑制现象。因此，通过对El和Er大小进行比较，可实现运动想象分类，即:

(8)

式(8)中，C为分类结果，“l”和“r”分别表示左手和右手运动想象。

2 实验结果与分析

2.1 实验数据

本文所采用的实验数据是2008年BCI 国际竞赛提供的公开数据集(BCI competition IV-2b)[6]。该数据集中包含9位被试者进行左、右手运动想象时采集的两类MI-EEG数据。每位被试提供5组数据(x_1T，x_2T，x_3T，x_4E，x_5E；x=1，…，9为受试者编号)，前三组作为训练集，后两组为测试集。后三组数据为同一实验范式下(提供MI控制结果的反馈信息)采集的数据。本文研究中，我们选择x_3T为训练集，x_4E，x_5E为测试集。每一数据集中含有3导联(C3，Cz，C4)运动皮层EEG数据，由160个单次试验组成(左、右手MI各80个)。单次试验的时间长度为8～9 s，采集过程如图3所示。

每次试验开始时(t=0)计算机屏幕中央出现一个灰色的笑脸，此后的2 s时刻(t=2 s)，一个短促“beep”声音提示受试者做好准备。MI类型提示在t=3 s出现在计算机屏幕上直到7.5 s结束。受试者在这段时间内按指定的运动类型进行左手或右手运动想象，此后MI提示消失，计算机屏幕变为空白，被试等待下一次单次试验开始。需要说明的是BCI competition IV-2b对参赛结果的评估标准是依据对两组测试集(x_4E，x_5E)的最优分类结果，并采用kappa值为量化评估指标[6]。

2.2 自测试实验

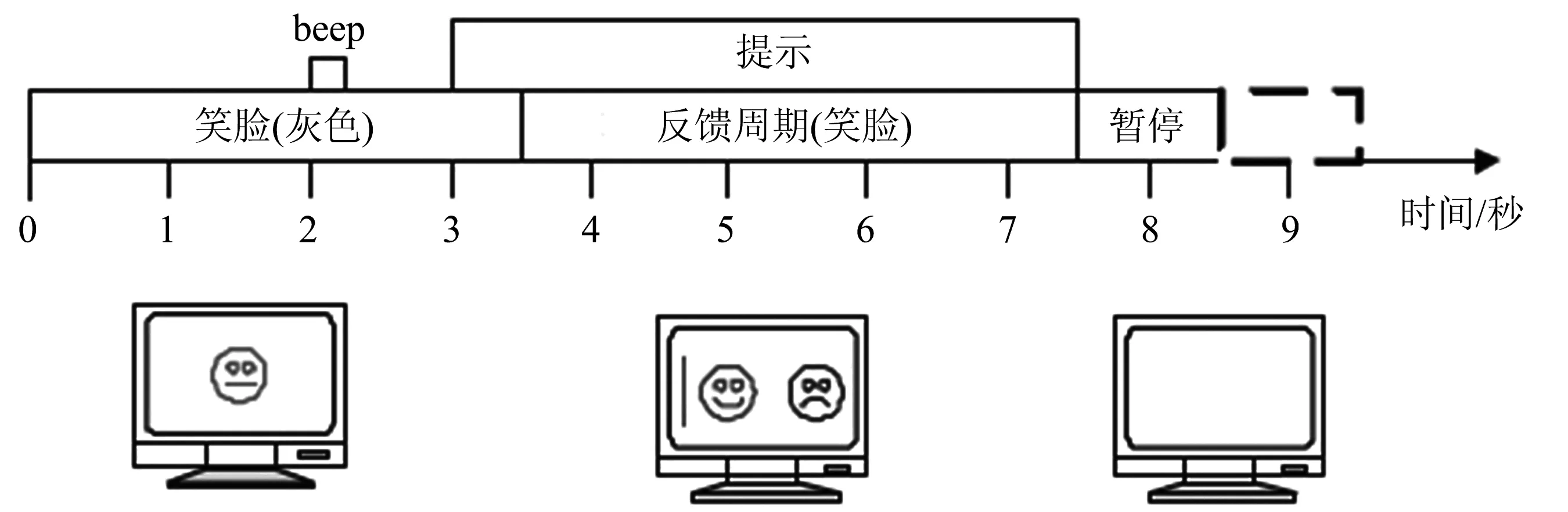
图3 单次MI实验的时间范式

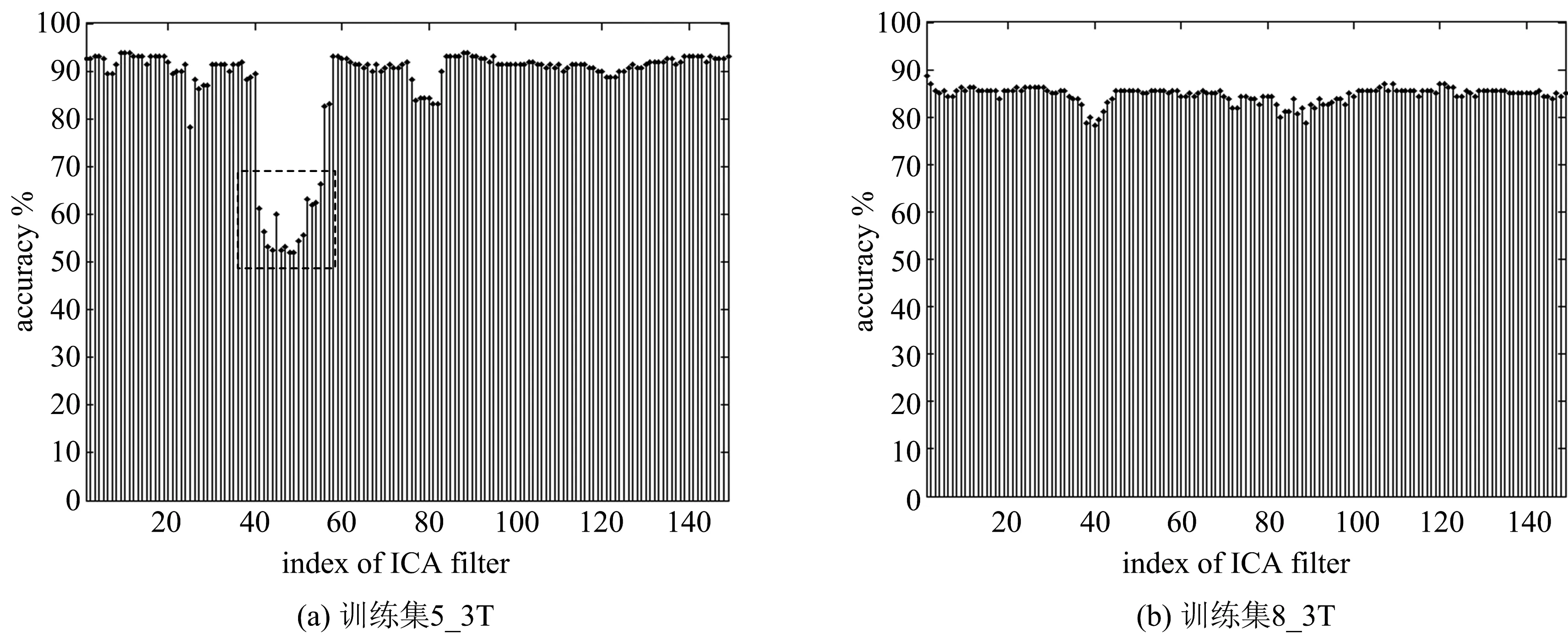
图4 自测试识别率结果

图5 受试者5的模型迁移测试结果

为了验证前述数据质量对ICA滤波器及其BCI性能的影响。本节依照图2给出的自测试算法流程，首先对第5和第8两位受试者测试集(5_3T，8_3T)进行了自测试。数据窗时宽T=96 s，数据窗滑动步长Ts=8 s，自测试识别率结果分别如图4(a)和图4(b)所示。根据图4(a)可以看到，在采用5_3T中某些EEG数据段设计ICA空域滤波器时，对应的自测试识别率明显降低(虚线方框标识)，表明该数据集中的部分数据段含有较严重的干扰成分。相比较而言，图4(b)所示识别率虽然也有一定的波动，但总体平稳，表明8_3T不含有被严重干扰的数据段。不难理解，在预处理、特征提取、分类方法和测试集等完全相同的前提下，自测试识别率的波动显然与ICA滤波器在性能方面的差异有直接关系，但根本原因还是ICA设计样本的差异。为了进一步验证样本质量、ICA滤波器性能和BCI识别率三者之间的关系，我们基于受试者5的三组数据集，进行模型迁移测试，其步骤与自测试基本一致，不同之处在于，测试集不再是5_3T自身，而是5_4E和5_5E。图5给出了基于5_4E和5_5E的迁移测试识别率。可以看到，图5图(a)(b)迁移测试识别率与4(a)所示的自测试识别率在变化趋势上具有很高的一致性。这一结果对ICA滤波器性能评估和优化选择具有实际意义。我们可根据训练集的自测试结果，选用与最大自测试识别率对应的ICA空域滤波器[wl，wr]构建MI-BCI系统，也可以根据自测试识别率，选择更多高质量的训练样本，进一步优化设计ICA滤波器，这样可有效避免低质量训练数据参与ICA-BCI系统的设计和训练，确保ICA-BCI系统具有良好稳定的性能。

2.3 全部数据的迁移测试

图6 九位受试者训练数据的自测试结果：(a)-(i)对应受试者1-9

图6给出了全部9位受试者训练集数据(x_3T，x=1，…，9)的自测试结果。在后续模型迁移测试中，分别从图6所示的9组自测试结果中，选择最大识别率对应的ICA空域滤波器[wl，wr]i，i=1，…，9构建相应的ICA-BCI系统，然后对每位受试者的两组测试数据(x_4E，x_5E，x=1，…，9)进行模型迁移识别率测试，所得结果如表2所示。考虑到BCI竞赛以两组测试集的最高识别为评估标准，所以表2最后一行列出了两组识别正确率结果中的最大值，并同时给出了相应的kappa值(见表3)。识别正确率(Acc)和kappa值(Ka)的换算关系如(9)式所示。为了便于比较，表3中列出了针对该组数据的BCI竞赛第一名的结果。

表2 九位被试数据的迁移识别率(%)(训练数据x_3T，测试数据为x_4E，x_5E)

表3 本文结果与BCI竞赛第一名结果比较(kappa值)

(9)

根据表3可知，使用本文所提算法对4位被试(1，4，5，6)测试集的分类结果优于BCI竞赛第一名的结果，其中在对被试6的MI分类中，本文方法优势明显(kappa值提升27.8%)。两方法对被试(7，9)的测试结果相同。两种方法应用于全部被试数据的平均kappa值分别为0.62和0.6，总体上，本方法要优于BCI竞赛第一名所采用的方法。

2.4 讨论

根据已公布的BCI competition IV-2b竞赛结果和参赛者所使用的方法[6]，竞赛第一名获得者采用了基于滤波器组的共同空间模式方法(FBCSP)[14]。竞赛第二名获得者则采用基于多时/频窗口的特征向量提取和分类方法。从所用特性向量维数和运算复杂度方面来看，竞赛所用方法显然要高于本文所提方法，但本文方法却获得了更高的识别率结果。

目前，CSP是MI-BCI系统实现主要采用的空域滤波算法。CSP空域滤波器虽然理论上具有最佳可区分性，但其不足之处也比较明显，例如，CSP设计所需的大量标签样本采集是一件比较困难的工作，用户通常需要长时间观察计算机屏幕提示进行运动想象，因此极易出现疲劳和精力分散问题，由此而产生的低质量训练样本是很难通过人工检查方式发现的[15]。到目前为止，低质量的训练样本所导致的CSP滤波器的稳定性和可迁移性较差问题还难以有效克服[16]。本文采用的ICA方法是一种无监督设计方法。ICA空域滤波器的设计不依赖运动类型标签，因此，训练样本采集要容易得多。在正式操作前，用户可在安静状态下采集ICA滤波器设计所需EEG样本。特别是导联较少的情况下，100秒左右的连续EEG样本基本能满足设计要求。虽然ICA滤波器也可能会因强干扰或者电极故障而出现性能下降(如图4(a)，图5所示)，但其优化调整相对方便。从图6所示自测试结果可以看到，正常情况下，采用不同数据段设计的ICA滤波器的性能基本稳定。因此，如果出现识别率或控制效果异常，通常只需受试者在静息状态下重新采集一段100秒左右的EEG训练样本即可(注：静息状态下，可有效减少不自主运动引起的电极故障和突发强干扰)[3，13]。另外，较少EEG导联的使用，不仅会明显降低出现电极干扰和电极故障的发生概率，也有利于降低系统实现和维护作成本。

3 结语

针对少量导联情况下MI-BCI系统的可实现性开展研究，提出了一种基于ICA的MI-BCI系统构建方案。实验结果表明，所提方法具有良好的运动想象分类性能和较低的运算复杂度，因此具有实际应用潜力。所提方法的特色体现于ICA空域滤波器的无监督优化设计思路。基于该思路所建立的MI-BCI系统实现方法具有一定的实际应用价值。此外，本文研究结果验证了在少量导联EEG情况下，ICA方法依然能起到信噪比改善效果，为ICA在MI-BCI系统实现中的合理运用提供了有价值的参考。